Tag: Fractal Dimension

Cantor Sets, Sierpinski Carpets, Menger Sponges

Cantor Sets, Sierpinski Carpets, Menger Sponges

Key Terms

  • Cantor Sets
  • Sierpinski Carpets
  • Menger Sponges
  • Fractals
  • Dimension
  • Georg Cantor
  • Waclaw Sierpinski
  • Karl Menger
  • 3 Steps of Vishnu
  • Maha Maya
  • Space Time Geometry
  • Fractal Space Time
  • Cantorian Space Time
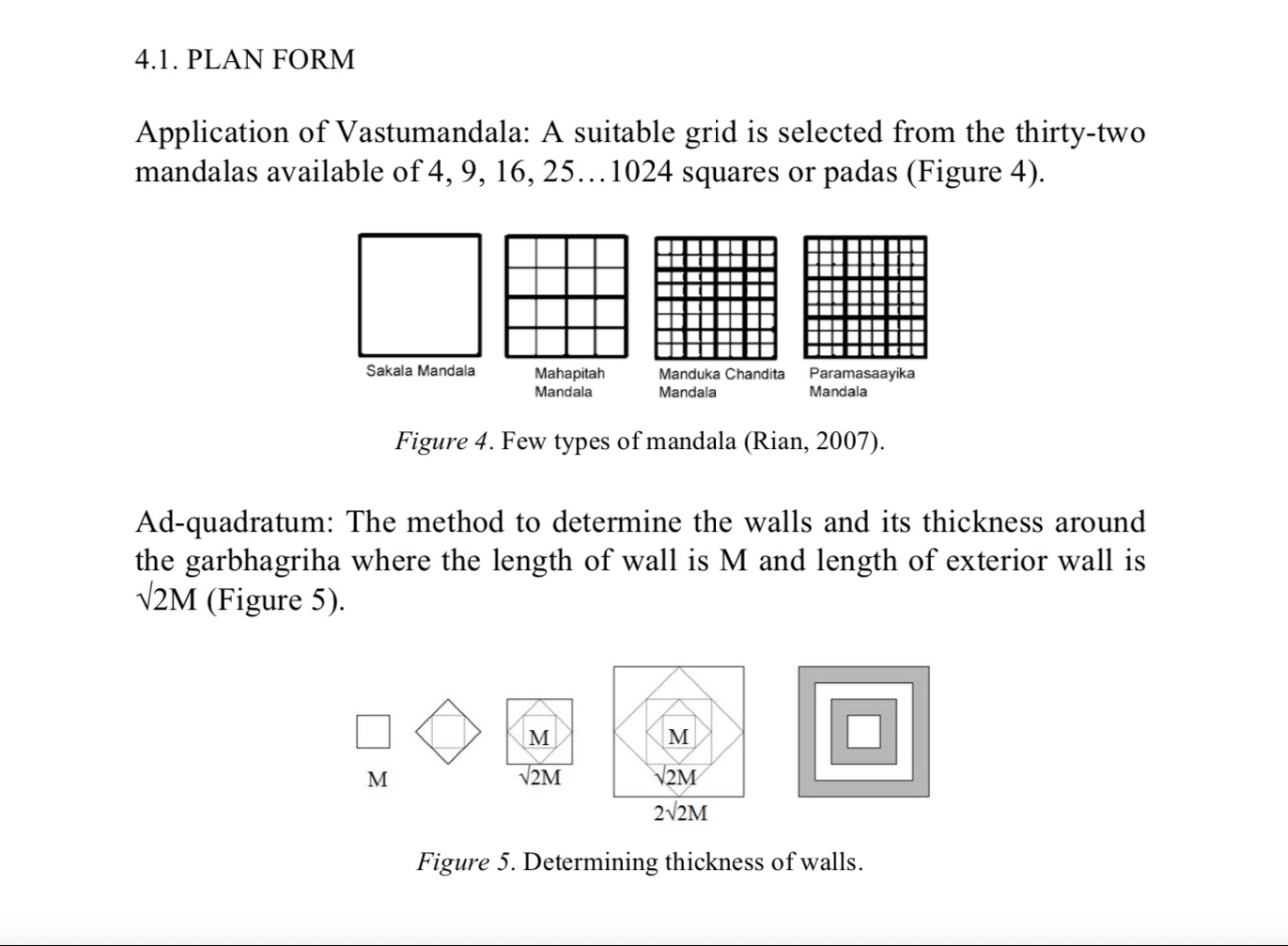
  • 9 x 9 square
  • 8 x 8 square
  • 18 and 81
  • 56 and 65 (64 + 1)
  • Chhapan Bhog
  • Chousath Kala
  • Chousath Yogini
  • Fractal Dimension
  • Noninteger Dimension
  • Euler’s Number
  • 64 Tetrahedron
  • Kal Bhairav
  • Kali
  • Geometry of Space Time
  • Truncated Icosahedron
  • Soccer Ball Geometry
  • Pentagon and Hexagon
  • 9 Planets
  • 27 Nakshatras
  • 14 Lokas
  • Hausdorff Dimension
  • Non Commutative Geometry

Cantor Sets, Sierpinski Carpets, Menger Sponges

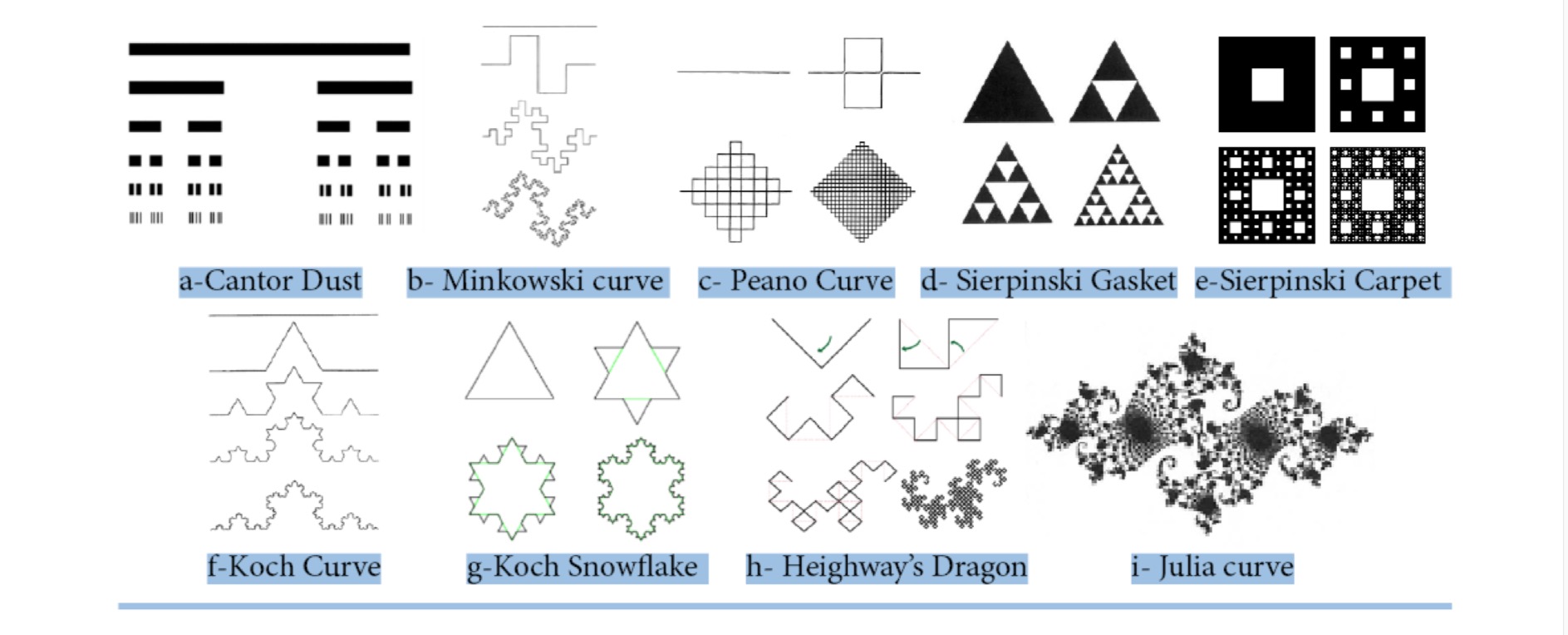
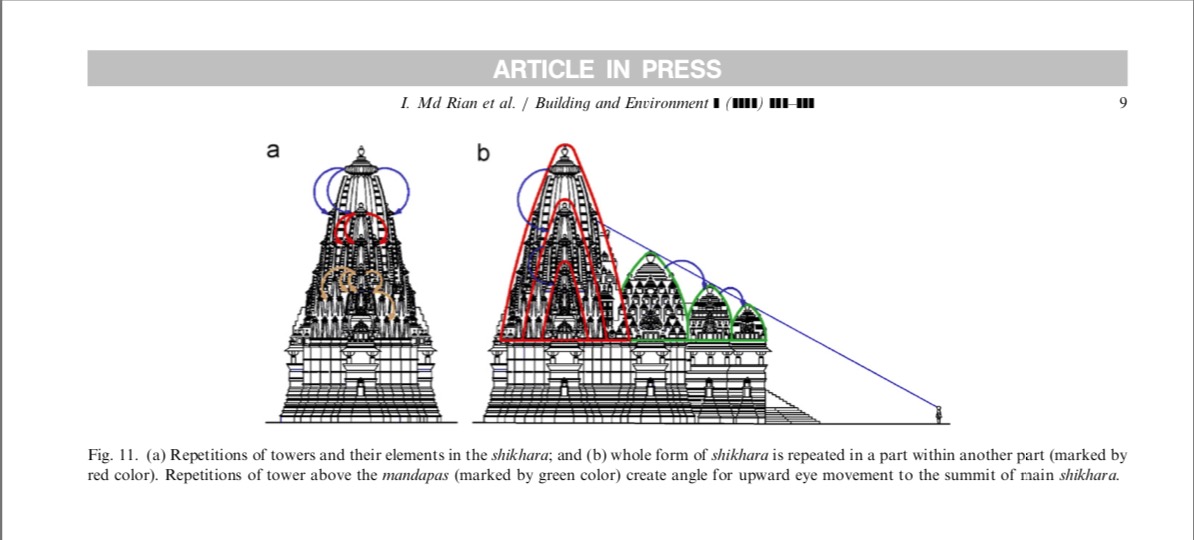
  • The Menger Sponge is formed by removing cubes from the original cube in an iterative manner.
  • This fractal has dimension d = log 20 / log 3 = 2.7268 placing
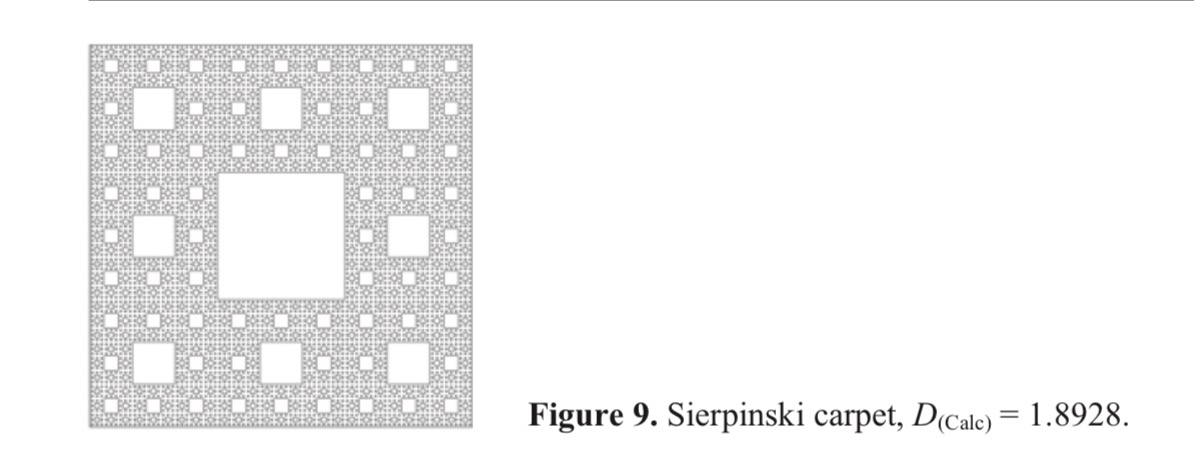
    it a space between two and three dimensions.
  • The Sierpinski carpet has fractal dimension = log 8/ log 3 = 1.8928.
  • The fractal dimension of the ternary Cantor set is DH = ln(2)/ln(3) = 0.6309.

Source: A Short History of Fractal Dimension

Source: A Short History of Fractal Dimension

Source: A Short History of Fractal Dimension

Source: A Short History of Fractal Dimension

Source: A Short History of Fractal Dimension

Source: A Short History of Fractal Dimension

Source: Menger Universal Spaces: Introduction to Fractal Geometry and Chaos

Source: Menger Universal Spaces: Introduction to Fractal Geometry and Chaos

Source: Menger Universal Spaces: Introduction to Fractal Geometry and Chaos

Source: Fractals: The Menger Sponge

Source: THE UNIVERSALITY OF THE HYPERPOLAR IMAGES OF THE SIERPINSKI CARPET AND THE MENGER SPONGE

Source: THE UNIVERSALITY OF THE HYPERPOLAR IMAGES OF THE SIERPINSKI CARPET AND THE MENGER SPONGE

Source: THE UNIVERSALITY OF THE HYPERPOLAR IMAGES OF THE SIERPINSKI CARPET AND THE MENGER SPONGE

Source: Mathematical Impressions: The Surprising Menger Sponge Slice

Source: Mathematical Impressions: The Surprising Menger Sponge Slice

Source: Mathematical Impressions: The Surprising Menger Sponge Slice

Source: Mathematical Impressions: The Surprising Menger Sponge Slice

Source: Mathematical Impressions: The Surprising Menger Sponge Slice

Source: Mathematical Impressions: The Surprising Menger Sponge Slice

Space, Fractal Spacetime, Cantorian Spacetime in Cosmology

Prof. M. S. El Naschie has published many research papers on Fractal Spacetime, Cantorian Spacetime, Dark Energy, and structure and geometry of space.

Please see references.

Source: A Fractal Menger Sponge Space-Time Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy

My Related Posts

Growth and Form in Nature: Power Laws and Fractals

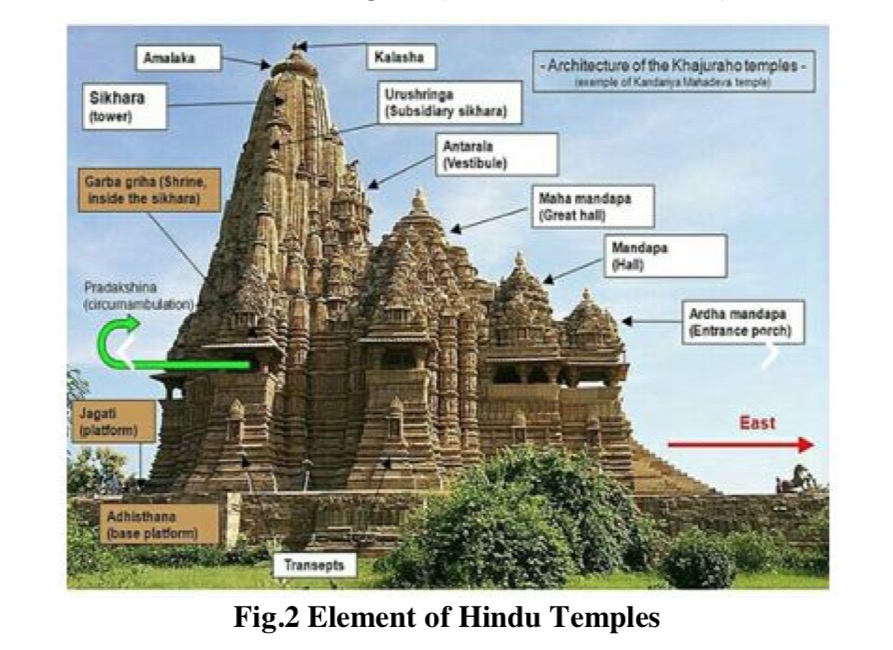
Fractal Geometry and Hindu Temple Architecture

Indra’s Net: On Interconnectedness

Shapes and Patterns in Nature

Shape of the Universe

Cosmic Mirror Theory

Consciousness of Cosmos: A Fractal, Recursive, Holographic Universe

Geometry of Consciousness

Maha Vakyas: Great Aphorisms in Vedanta

The Great Chain of Being

Interconnected Pythagorean Triples using Central Squares Theory

Myth of Invariance: Sound, Music, and Recurrent Events and Structures

The Pillar of Celestial Fire

Key Sources for Research

Mathematical Impressions: The Surprising Menger Sponge Slice

Simons Foundation

Menger Universal Spaces

Introduction to Fractal Geometry and Chaos

Matilde Marcolli

MAT1845HS Winter 2020, University of Toronto

Click to access FractalsUToronto7.pdf

Fractals: The Menger Sponge

Click to access twg00866-lesson-plan.pdf

LCAO approximation for scaling properties of the Menger sponge fractal

Kazuaki Sakoda

Optics Express Vol. 14, Issue 23, pp. 11372-11384 (2006) • https://doi.org/10.1364/OE.14.011372

https://opg.optica.org/oe/fulltext.cfm?uri=oe-14-23-11372&id=117895

Squeezing Pi from a Menger Sponge

Ed Pegg, Wolfram Research 

https://community.wolfram.com/groups/-/m/t/822984

mrly fractals

Inspired by Carlo Mats Vincenti Mitchener
Graphics by Paul Bourke
December 2022

http://paulbourke.net/fractals/mrlymath/index.html

Marley Math: Cantor Sets, Sierpinski Carpets, Menger Sponges, And More

Carlo Mats Vincenti Mitchener

24 April 2022

Click to access mrlymath.pdf

A Fractal Menger Sponge Space-Time Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy

Mohamed S. El Naschie

Department of Physics, University of Alexandria, Egypt

Email: Chaossf@aol.com

International Journal of Modern Nonlinear Theory and Application
Vol. 2  No. 2 (2013) , Article ID: 32969 , 15 pages

 DOI:10.4236/ijmnta.2013.22014

https://www.scirp.org/html/1-2340074_32969.htm

The Mystery of the Menger Sponge

NY Times

2011

New Classes of Regular Symmetric Fractals.

Kak, Subhash (2021):

TechRxiv. Preprint. https://doi.org/10.36227/techrxiv.14714094.v2 

THE GENERALIZATION OF SIERPINSKI CARPET AND MENGER SPONGE IN n-DIMENSIONAL SPACE

YUN YANG, 

YUTING FENG and 

YANHUA YU

https://doi.org/10.1142/S0218348X17500402

Fractals

Vol. 25, No. 05, 1750040 (2017)

https://www.worldscientific.com/doi/10.1142/S0218348X17500402

Hausdorff Measures and Hausdorff Dimensions of the Invariant Sets for Iterated Function Systems of Geometric Fractals

Md. Jahurul Islam1,*, Md. Shahidul Islam1, Md. Shafiqul Islam2

1Department of Mathematics, University of Dhaka, Bangladesh
2School of Mathematics and Computational Science, University of Prince Edward Island, Canada

Mathematics and Statistics 6(3): 25-33, 2018

DOI: 10.13189/ms.2018.060301

Click to access MS1-13411891.pdf

Sound absorption by Menger sponge fractal

Tetsuji Kawabea), Takatsuna Miyazakib), Daisuke Oka, Sin’ichiro Koyanagic), and Atsushi Hinokidani

The Journal of the Acoustical Society of America 125, 2830 (2009); https://doi.org/10.1121/1.3095807

https://asa.scitation.org/doi/full/10.1121/1.3095807

Fractal Dimensions in Circular and Spiral Phenomena.

Kak, Subhash (2022):

TechRxiv. Preprint. https://doi.org/10.36227/techrxiv.21766706.v1 

Sierpinski Carpets as Julia sets for Imaginary 3-Circle Inversions

Daniel M. Look

Williams College

Is Spacetime Fractal and Quantum Coherent in the Golden Mean?

Mae-Wan Ho , Mohamed el Naschie & Giuseppe Vitiello

Global Journal of Science Frontier Research

Volume XV Issue I Version I Year 2015

Real Analysis: The Sierpinski Carpet and its Remarkable Area Explained

Analysis on the Sierpinski Carpet

M. T. Barlow

Centre de Recherches Mathematiques

CRM Proceedings and Lecture Notes

Click to access sm4.pdf

Homeomorphisms of the Sierpinski Carpet

Karuna S. Sangam
Bard College, ks4217@bard.edu

Senior Projects Spring 2018

Bard Undergraduate Senior Projects

Click to access KarunaSangam.pdf

A SIERPINSKI CARPET LIKE FRACTAL WITHOUT STANDARD SELF-SIMILAR ENERGY

SHIPING CAO AND HUA QIU

Click to access 2109.12760.pdf

The construction of brownian motion on the Sierpinski carpet

MARTIN T. BARLOW 

RICHARD F. BASS

Annales de l’I. H. P., section B, tome 25, no 3 (1989), p. 225-257 

Click to access AIHPB_1989__25_3_225_0.pdf

Sierpinski

https://gofiguremath.org/fractals/sierpinski/

On the Hausdorff dimension of general Cantor sets,

A. F . Beardon,

Proc. Camb. Phil. Soc, 61 (1965), 679-694.

“Sur une courbe cantorienne qui contient une image biunivoque et continue de toute courbe donne”

W. Sierpiήski,

Comptes Rendus, 162 (1916), 629-642.

THE HAUSDORFF DIMENSION OF GENERAL SIERPINSKI CARPETS

CURT McMULLEN

Nagoya Math. J. Vol. 96 (1984), 1-9

Uniqueness of Brownian motion on Sierpinski carpets. 

Richard F. Bass, Takashi Kumagai, Martin T. Barlow, Alexander Teplyaev, 

J. Eur. Math. Soc. 12 (2010), no. 3, pp. 655–701

DOI 10.4171/JEMS/211

https://ems.press/journals/jems/articles/3456

GEODESICS IN THE SIERPINSKI CARPET AND MENGER SPONGE

ETHAN BERKOVE and DEREK SMITH

Fractals

Vol. 28, No. 07, 2050120 (2020)
https://doi.org/10.1142/S0218348X20501200

https://www.worldscientific.com/doi/10.1142/S0218348X20501200

The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review).

El Naschie, M.S. (2009)

Chaos, Solitons & Fractals, 41, 2635-2646. 
http://dx.doi.org/10.1016/j.chaos.2008.09.059

The Ultimate Unified Physico Mathematical Theory of Nature

M.S. El Naschie

Distinguished Professor, Department of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt.

Date of publication (dd/mm/yyyy): 22/08/2022

International Journal of Innovation in Science and Mathematics

Volume 10, Issue 4, ISSN (Online): 2347–9051

Click to access IJISM_974_FINAL.pdf

Analysis on Fractal Objects

Uta Freiberg
Technische Universität Chemnitz

December 2005

Meccanica 40(4):419-436
DOI:10.1007/s11012-005-2107-0

https://www.researchgate.net/publication/226551998_Analysis_on_Fractal_Objects

Exponentially Decaying Discrete Dynamical Systems

Yogesh Joshi
CIty University of New York – Kingsborough Community College

Denis Blackmore
New Jersey Institute of Technology

April 2012

Recent Patents on Space Technology 2(1):37-48
DOI:10.2174/1877611611202010037

https://www.researchgate.net/publication/267391812_Exponentially_Decaying_Discrete_Dynamical_Systems


THE UNIVERSALITY OF THE HYPERPOLAR IMAGES OF THE SIERPINSKI CARPET AND THE MENGER SPONGE

Glaser, F. (1997, Fall).

The Cal Poly Pomona Journal of Interdisciplinary Studies, 10, 9-18.

https://scholarworks.calstate.edu/downloads/gx41mk81q?locale=es

EVALUATING THE EXACT INFINITESIMAL VALUES OF AREA OF SIERPINSKI’S CARPET AND VOLUME OF MENGER’S SPONGE

Yaroslav D. Sergeyev∗

Dipartimento di Elettronica, Informatica e Sistemistica, Universita` della Calabria, Via P. Bucci, Cubo 42-C, 87030 Rende (CS) – Italy

http://wwwinfo.deis.unical.it/∼yaro yaro@si.deis.unical.it

Chaos, Solitons & Fractals
Volume 42, Issue 5, 15 December 2009, Pages 3042-3046

Click to access 1203.3150.pdf

https://www.sciencedirect.com/science/article/abs/pii/S0960077909003877

Click to access Extensions.pdf

Dynamics of fractals in Euclidean and measure spaces

Md. Shahidul Islam and Md. Jahurul Islam 2017

 J. Phys.: Conf. Ser. 890 012058

https://iopscience.iop.org/article/10.1088/1742-6596/890/1/012058/pdf

Cantor sets

March 2010

Ferdinand Chovanec
Armed Forces Academy of General Milan Rastislav Štefánik

https://www.researchgate.net/publication/228747023_Cantor_sets

Generalizations and Properties of the Ternary Cantor Set and Explorations in Similar Sets

by Rebecca Stettin

Ashland University

May 2017

https://etd.ohiolink.edu/apexprod/rws_etd/send_file/send?accession=auhonors1494171314877262&disposition=inline

Study of Variants of Cantor Sets Using Iterated Function System

Gen. Math. Notes, Vol. 23, No. 1, July 2014, pp. 45-58

https://www.semanticscholar.org/paper/Study-of-Variants-of-Cantor-Sets-Using-Iterated-Rani-Chugh/a110f82b7bf693815b53d97ad1ae8e74eb99c7c4

Click to access 6_GMN-4682-V23N1.247122947.pdf

Volume of the hyperbolic cantor sets

Habibulla Akhadkulov & Yunping Jiang (2020) 

Dynamical Systems, 35:2, 185-196, 

DOI: 10.1080/14689367.2019.1659754

https://www.tandfonline.com/doi/full/10.1080/14689367.2019.1659754

THE GENERALIZED CAPACITY OF CANTOR SETS

A. F. BEARDON

The Quarterly Journal of Mathematics, Volume 19, Issue 1, 1968, Pages 301–304, https://doi.org/10.1093/qmath/19.1.301

https://academic.oup.com/qjmath/article-abstract/19/1/301/1570320?redirectedFrom=PDF

Box-Counting Dimension of the Cantor Set

https://users.math.yale.edu/public_html/People/frame/Fractals/FracAndDim/BoxDim/CantorBoxDim/CantorBoxDim.html

A Note on the History of the Cantor Set and Cantor Function

JULIAN F. FLERON 

SUNY at Albany

Albany, New York

Mathematics Magazine, Vol. 67, No. 2 (Apr., 1994), pp. 136-140

Published by: Mathematical Association of America
Stable URL: http://www.jstor.org/stable/2690689 .

Click to access julian-f-fleron-a-note-on-the-history-of-the-cantor-set-and-cantor-function.pdf

Cantor Set and Its Properties

Zhixing Guo
University of California, Santa Barbara

April 23, 2014

Click to access mathcs103_s2014_zhixing_presentation.pdf

The Cantor Set and the Cantor Function

TMA4225 – Foundations of Analysis

Click to access cantor_set_function.pdf

On the measure of arithmetic sums of Cantor sets

Boris Solomyak∗
Department of Mathematics, University of Washington, USA

Indagationes Mathematicae
Volume 8, Issue 1, 1997, Pages 133-141

https://www.sciencedirect.com/science/article/pii/S0019357797833575

Multi Dimensional Cantor Sets in Classical and Quantum Mechanics

M. S. EL NASCHIE

Chaos, Solitons & Fractals Vol. 2, No. 2. pp.211-220. 1992

https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=b726b523ca21eea5d3b05bd27062f52bd8c34a98

An Exploration of the Cantor Set

Christopher Shaver
Rockhurst University, shaverc@hawks.rockhurst.edu

Rose-Hulman Undergraduate Mathematics Journal: Vol. 11 : Iss. 1 , Article 1.

2010

https://scholar.rose-hulman.edu/cgi/viewcontent.cgi?article=1115&context=rhumj

An Exact Mathematical Picture of Quantum Spacetime

Mohamed S. El Naschie

Department of Physics, University of Alexandria, Alexandria, Egypt Email: Chaossf@aol.com

Advances in Pure Mathematics, 2015, 5, 560-570

http://dx.doi.org/10.4236/apm.2015.59052

https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/journal/paperinformation.aspx?paperid=57895

On El Naschie’s Fractal-Cantorian Space-Time and Dark Energy—A Tutorial Review

Leila Marek-Crnjac

Department of Mathematics, Technical School Center of Maribor, Maribor, Slovenia

Natural Science, 2015, 7, 581-598

http://dx.doi.org/10.4236/ns.2015.713058

https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/journal/paperinformation.aspx?paperid=61825

High Energy Physics and Cosmology as Computation. 

El Naschie, M. (2016)

American Journal of Computational Mathematics, 6, 185-199.

doi: 10.4236/ajcm.2016.63020.

https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/journal/paperinformation.aspx?paperid=67938

On the Need for Fractal Logic in High Energy Quantum Physics. 

Naschie, M. , Olsen, S. , He, J. , Nada, S. , Marek-Crnjac, L. and Helal, A. (2012)

International Journal of Modern Nonlinear Theory and Application, 1, 84-92.

doi: 10.4236/ijmnta.2012.13012.

https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/journal/paperinformation.aspx?paperid=23087

Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry

M. El Naschie

Journal of Quantum Information Science, Vol. 1 No. 2, 2011, pp. 50-53.

doi: 10.4236/jqis.2011.12007.

https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/journal/paperinformation.aspx?paperid=7623

The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology

M. A. Helal, L. Marek-Crnjac and J. He,

Open Journal of Microphysics, Vol. 3 No. 4, 2013, pp. 141-145.

doi: 10.4236/ojm.2013.34020.

https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/journal/paperinformation.aspx?paperid=39841

An Exact Mathematical Picture of Quantum Spacetime. 

Naschie, M. (2015)

Advances in Pure Mathematics, 5, 560-570.

doi: 10.4236/apm.2015.59052.

https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/journal/paperinformation.aspx?paperid=57895

A guide to the mathematics of E-infinity Cantorian spacetime theory


El Naschie, M. S.

Chaos, Solitons and Fractals, Volume 25, Issue 5, p. 955-964.
Pub Date: September 2005

DOI: 10.1016/j.chaos.2004.12.033

https://www.sciencedirect.com/science/article/abs/pii/S0960077905000688?via%3Dihub

Dimensional symmetry breaking, information and fractal gravity in Cantorian space.

el Naschie MS.

Biosystems. 1998 Apr;46(1-2):41-6.

doi: 10.1016/s0303-2647(97)00079-8. PMID: 9648673.

https://pubmed.ncbi.nlm.nih.gov/9648673/

Time Symmetry Breaking, Duality and Cantorian Space-Time

M. S. EL NASCHIE DAMTP, Cambridge, UK

Chaos, Solitons & Fractals Vol 7. No. 4, pp. 499 – 518, 1996

Click to access 5.Time%20Symmetry%20Breaking,%20Duality.pdf

Renormalization Approach to the Dimension of Diffusion in Cantorian Space

M. S. EL NASCHIE

Appl. Math. Lett. Vol. 8, No. 1, pp. 59-63, 1995

Click to access 82010128.pdf

On the Missing Link between Cosmology and Biology 

Mohamed S. El Naschie1, Scott Olsen2, M.A. Helal3, L. Marek-Crnjac4 and S. Nada

International Journal of Innovation in Science and Mathematics

Volume 6, Issue 1, ISSN (Online): 2347–9051

Click to access MissingLinkbetweenCosmologyandBiology.pdf

Information theory and dimensionality of space. 

Kak, S.

Sci Rep 10, 20733 (2020).

https://doi.org/10.1038/s41598-020-77855-9

https://www.researchgate.net/publication/346540015_Information_theory_and_dimensionality_of_space

https://www.nature.com/articles/s41598-020-77855-9

The Ontology of Space

Subhash Kak

2021, Chapman University

https://www.academia.edu/49175956/The_Ontology_of_Space

https://www.academia.edu/49175956/The_Measure_of_Space

Our e-dimensional universe

Subhash Kak
Nov 27, 2020

https://subhashkak.medium.com/our-e-dimensional-universe-febb3a20fa64

Black holes, disk structures, and cosmological implications in e-dimensional space


Kak, Subhash ; Kafatos, Menas

Physics Essays, vol. 35, issue 4, pp. 345-355
Pub Date: December 2022

DOI: 10.4006/0836-1398-35.4.345

https://www.ingentaconnect.com/content/pe/pe/2022/00000035/00000004/art00004;jsessionid=1ngq6d7uavci8.x-ic-live-03

Asymptotic freedom and noninteger dimensionality.

Kak S.


Scientific Reports, 09 Feb 2021, 11(1):3406
DOI: 10.1038/s41598-021-83002-9 PMID: 33564046 PMCID: PMC7873067

https://europepmc.org/article/pmc/pmc7873067

On the dimensionality of spacetime

Max Tegmark†
Institute for Advanced Study, Olden Lane, Princeton, NJ 08540, USA

Received 10 February 1997

Class. Quantum Grav. 14 (1997) L69–L75

Click to access dimensions.pdf

The Topology and Combinatorics of Soccer Balls

Dieter Kotschick

American Scientist, Volume 94

Click to access soccerball_topology.pdf

A Short History of Fractal Dimension

DECEMBER 26, 2020 by David D. NOLTE

https://galileo-unbound.blog/2020/12/26/a-short-history-of-fractal-dimension/

Box counting fractal dimension of volumetric data

Written by Paul Bourke
April-May 2014

http://paulbourke.net/fractals/cubecount/

Fractal Geometry and Hindu Temple Architecture

Fractal Geometry and Hindu Temple Architecture

Source: Mandapa: Its Proportion as a tool in Understanding Indian Temple Architecture

Proportion and measurements were the guiding tools for Indian temple construction starting from the 5th century onwards and it continuous even now. Through out the history proportion dominated as a tool, which determined the monuments both spatial arrangements as well as form. The ancient texts, therefore, insist on a high degree of precision in their measurements.

The standard text Mayamata mentions- ”Only if the temple is constructed correctly according to a mathematical system can it be expected to function in harmony with the universe. Only if the measurement of the temple is in every way perfect, there will be perfection in the universe as well.”

Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

Source: TEMPLE ARCHITECTURE AND SCULPTURE

Source: Symbolism in Hindu Temple Architecture and Fractal Geometry – ‘Thought Behind Form’

Source: TEMPLE ARCHITECTURE AND SCULPTURE

Source: TEMPLE ARCHITECTURE AND SCULPTURE

Key Terms

  • Fractals
  • Cosmology
  • Temple Architecture
  • Fractal Dimension
  • Recursive
  • Algorithmically
  • Hindu Temples
  • Vastu Purush Mandala
  • Vastu Shastra
  • Shilpa Shastra
  • Nagara Style
  • Dravidian Style
  • Vesara Style
  • Kalinga Style
  • 64 Yogini Temple Style
  • Jain Temple Architecture
  • Buddhist Stupa Architecture
  • Cellular Automata
  • 3D Fractals
  • 2D Cellular Automata
  • Nine Cell Square
  • Nav Grah Yantra
  • Sierpinski Carpet
  • Box Counting Method
  • Biophilic Architecture
  • Symbolism
  • Square and Circle
  • Earth and Heaven
  • Squaring the Circle
  • Correspondence
  • Equivalence
  • Symmetry
  • As Above, So below
  • Cosmic Mirrors

Hindu Temples: Models of a Fractal Universe

Source: Hindu temples: Models of a fractal universe

Hindu philosophy views the cosmos to be holonomic and self-similar in nature. According to ancient architectural tradition, Hindu temples are symbols of models of the cosmos and their form represents the cosmos symbolically.

The procedures and methods used in the construction of Hindu temples bear a striking resemblance to the procedures of computer graphics, including discretization, fractalization and extensive use of recursive procedures, including self-similar iteration. The instructions given in ancient Vastu shastras (texts on architecture) work like general programmes to generate various types of temples.

The paper is an attempt to draw attention to the similarities between the procedures and resulting forms in computer graphics and Hindu temple architecture and to explain the relationship that exists between the form of the temple and the concepts of Hindu philosophy. It is proposed that Hindu temples may be viewed as three dimensional fractal models and that the use of fractal geometry procedures has a special symbolic meaning in the generation of the forms of Hindu temples.

Introduction to the Temple Architecture in the Indian Context

Source: Temples of Odisha- the Geometry of Plan Form

The evolution of temple architecture is marked by a strict adherence to the original ancient models, that were derived from sacred thought which persisted over many centuries. The commencement of the main style of Hindu temple architecture in India dates back to the Mauryan period i.e 3rd century BC, as evident from the archaeological excavation at Sanchi (Madhya Pradesh, temple no.40 and18) and Bairat (Rajastan), (DB Garnayak , 2007) . The Indian Silpasastras recognize three main types of temples known as the Nagara, Dravida and Vesara. Nagara temple belongs to the country from the Himalaya to the Vindhya, Vesara from the Vindhya to the Krishna and the Dravida from the Krishna to the Cape Comorin (DB Garnayak , 2007). An inscription in 1235 A.D in the mukhamandapa of the Amritesvara temple at Holal in Bellary district of Karnataka speaks of the fourth style i.e. Kalinga, in addition to the above three. The Kalinga style of Architecture is explained exclusively in the texts like Bhubana Pradip, Silpa Prakasa, Silpa Ratnakosha etc.

Source: Investigating Architectural Patterns of Indian Traditional Hindu Temples through Visual Analysis Framework

Source: Fractal Geometry as a source of innovative formations in interior design

Source: The fractal analysis of architecture: calibrating the box-counting method using scaling coefficient and grid disposition variables

Source: PARAMETRIZING INDIAN KARNATA-DRAVIDA TEMPLE USING GEOMETRY

Vastu purusha mandala

Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

Layout of a Hindu temple pursues a geometrical design known as vastu-purusha-mandala, the name of which is derived from the three vital components of the design namely Vastu meaning Vaas or a place of dwelling; Purusha, meaning the Universal principle; and Mandala meaning circle. Vastupurushamandala is a mystical diagram referred in Sanskrit as a Yantra. The symmetrical and self-repeating model of a Hindu temple demonstrated in the design is derived from the primary convictions, traditions, myths, fundamentality and mathematical standards. According to Vastupurushamandala, the most sacred and typical template for a Hindu temple is the 8×8 (64) grid Manduka Hindu Temple Floor Plan also referred as Bhekapada and Ajira. The layout displays a vivid saffron centre with intersecting diagonals which according to Hindu philosophy symbolises the Purusha. The axis of the Mandir is created with the aid of the four fundamentally significant directions and thus, a perfect square is created around the axis within the available space. This square which is circumscribed by the Mandala circle and divided into perfect square grids is held sacred. On the other hand, the circle is regarded as human and worldly that can be perceived or noticed in daily life such as the Sun, Moon, rainbow, horizon or water drops. Both the square and the circle support each other. The model is usually seen in large temples while an 81 sub-square grid is observed in ceremonial temple superstructures. Each square within the main square referred as „Pada‟ symbolise a specific element that can be in the form of a deity, an apsara or a spirit. The primary or the innermost square/s of the 64 grid model called Brahma Padas is dedicated to Brahman. The Garbhagruha or centre of the house situated in the Brahma Padas houses the main deity. The outer concentric layer to Brahma Padas is the Devika Padas signifying facets of Devas or Gods which is again surrounded by the next layer, the Manusha Padas, with the ambulatory. The devotees circumambulate clockwise to perform Parikrama in the Manusha Padas with Devika Padas in the inner side and the Paishachika Padas, symbolising facets of Asuras and evils, on the outer side forming the last concentric square. The three outer Padas in larger temples generally adorn inspirational paintings, carvings and images with the wall reliefs and images of different temples depicting legends from different Hindu Epics and Vedic stories. Illustrations of artha, kama, dharma and moksha can be found in the embellished carvings and images adorning the walls, ceiling and pillars of the temples.

Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

Source: VASTU PURUSHA MANDALA- A HUMAN ECOLOGICAL FRAMEWORK FOR DESIGNING LIVING ENVIRONMENTS

Source: Space and Cosmology in the Hindu Temple

Source: Exploring Ancient Architectural Designs with Cellular Automata

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

According to Hindu philosophy, the main goal of man’s life is to achieve the ultimate liberation from the illusionary world where he suffers from his endless rebirth. Krishna says in Bhagavad Gita,9 if man worships, devotes and meditates to the manifested form of the wholeness of infinity, and sees the truth of its manifestation; he will surpass the confusion of the never-ending cycles of rebirth in this physical world, and finally will assimilate with the God. 10 Hindu calls it moksha.11 It brings the ultimate peace and harmony in man’s life. But how one, from the physical world, can practice to realize this ultimate truth of the creation? Brihatsamhita12 and Sthapatyaveda13 give the solution as the temple which should act as the microcosm of the cosmos [9]. It should be the bridge for the man of physical world to the God of divine world [10].

To connect the physical world with the divine world and to reflect the truth of creation, the layout of cosmos was copied graphically in the foundation of temple. Here, a mythical incident was interwoven where a formless being covered the sky and was, immediately, arrested down to the earth by the creator Brahma and other gods. This supernatural fact was depicted graphically by vastu purusha mandala, where vastu refers to physical environment, purusha refers to energy, power or cosmic being, and mandala is the diagram or chart. Central portion of the mandala represents the place of Brahma and other portions symbolize the other gods according to their capability. By laying down this metaphysical diagram in the foundation, various supernatural forces are captured beneath the temple whereas its centre is the source of cosmic energies. The basic shape of the vastu purusha mandala is a square which represents the earth [11]. Its four sides depict the four cardinal directions. It also symbolizes the order, the completeness of endless life and the perfectness of life and death [10]. According to Hindu philosophy, our mundane life is controlled by the number four—four castes, four stages of life, four great epochs or mahayugas, four heads of Brahma, the four Vedas etc. [12].

There are various types of vastu purusha mandala, which are nothing but the squares grids, produced from the basic shape; namely, a square which is known as sakala mandala. Each smaller square within the grid is called one pada. The number of pada may vary from 1, 4, 9, 16, 25 and so on 1024, where it follows the geometric progression of 1, 2, 3, 4, 5,…..,32 of common ratio 2. The mandala having even numbers of pada in its grid known as yugma squares mandala whereas the mandala, having odd numbers of pada known as ayugma squares mandala. Vastu purusha mandala is also known as different distinctive names according to the numbers of pada within the grid. The mandala having 1,4,9,16,25 and 36 numbers of pada within the grid are known as sakala mandala, pechaka mandala, pitah mandala, mahapitah mandala, manduka chandita mandala and para- masayika mandala, respectively14.

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

FRACTAL DESIGN, ARCHITECTURE AND ART IN HUMAN HISTORY

Source: Working with Fractals

Fractals have permeated cultures spanning across many centuries and continents, classical art and vernacular architecture from the column capitals of ancient Greece, Egyptian, Aztec, Incan civilisations, the art of Ancient Mayans, Islamic and Hindu temples, Angkor Wat in Cambodia, the Eifel Tower in Paris, and the structures of Santiago Calatrava. Fractals are also evident in such well known works as those of Botticelli, Vincent van Gogh, and Jackson Pollock. Their visual properties were also explored by mathematicians when Benoit Mandelbrot published The Fractal Geometry of Nature (1982) in which he catalogued nature’s statistical fractals and discussed them using mathematical methods for their replication.

Fractals constitute a central component of human daily experience of the environment (Taylor & Spehar, 2016). While extensive research has documented the negative effects of environments that do not have
a complement of rich experiential aesthetic variety (Mehaffy & Salingaros, 2013), their proliferation in art and design has continued to grow and diversify, creating architecture, interiors and products designed for human needs (Taylor & Spehar, 2016). Over the past two decades, interdisciplinary teams have confirmed that the aesthetic qualities of nature’s fractal patterns can induce striking effects on health.1

PARAMETERS OF FRACTAL PREFERENCE

Source: Working with Fractals: For the Love of Fractals

The universal preference for ‘statistical’ fractals peaks at low to moderate degree of complexity, while universal preference for ‘exact’ fractals peaks at a higher complexity. The high level of symmetry in exact fractals enables greater tolerance for visual complexity compared to statistical fractals (Abboushi et al., 2019). Four factors influence complexity in exact fractals:

1. Fractal dimension (D)

2. Symmetry

3. Recursion

4. Number of elements introduced at each recursion

Fractal dimension. 

The Euclidean simplicity and symmetry of exact fractals increases tolerance and peak preference for medium-high complexity exact fractals (D= 1.5–1.7) (Abboushi et al., 2019). Medium- high exact fractals can enhance visual preference and mood, particularly in less complex Euclidean interior spaces (Abboushi et al., 2019; Taylor et al., 2018).

When complex fractal patterns are experienced within a low-complexity interior space, the visual preference can shift to those available higher D values (1.5 to 1.7, medium-high range), suggesting that a low complexity environment enables a tolerance and preference for higher complexity statistical fractals such as found in artworks or casted light patterns unique within that space (Abboushi et al., 2019). A good example of this scenario is museums with an abundance of geometrical rooms and white walls adorned with highly complex artworks that captivate.

Symmetry. 

Patterns with symmetry and geometry, such as common among exact fractals, can be visually appealing as they balance interest and comprehensibility. Mirror symmetry is generally considered one of the most predictive factors when judging whether a geometric pattern is ‘beautiful’. A lack of radial and mirror symmetry can be overcome by including more recursion and higher fractal dimensionality.

The orderliness of exact fractals allows a pattern to approach the maximum use of space at a particular dimension while retaining its elegance. Patterned tiles and carpet, wall coverings and textiles, artefacts and ornaments found in many cultures (Eglash, 2002) are evidence of this spatial orderliness and symmetry.

Recursion. 

Fractals generated by a finite subdivision rule bear a striking resemblance to both nature and human ornament. In mathematics, the finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. In a sense, subdivision rules are generalisations of regular exact fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals (Cannon, et al., 2001).

Source: The application of complexity theory and Fractals in architecture, urban planning and design

Source: The application of complexity theory and Fractals in architecture, urban planning and design

My Related Posts

Shapes and Patterns in Nature

Shape of the Universe

Cosmic Mirror Theory

Interconnected Pythagorean Triples using Central Squares Theory

Indra’s Net: On Interconnectedness

The Great Chain of Being

Maha Vakyas: Great Aphorisms in Vedanta

Growth and Form in Nature: Power Laws and Fractals

Geometry of Consciousness

Consciousness of Cosmos: A Fractal, Recursive, Holographic Universe

Mind, Consciousness and Quantum Entanglement

Meta Integral Theories: Integral Theory, Critical Realism, and Complex Thought

From Systems to Complex Systems

The Pillar of Celestial Fire

Key Sources of Research:

Role of Fractal Geometry in Indian Hindu Temple Architecture

Dhrubajyoti Sardar
M.Arch Scholar
Architecture & Planning Department, IIT Roorkee

Roorkee, Uttarakhand, India

S. Y. Kulkarni
Professor & Former Head Architecture & Planning Department, IIT Roorkee Roorkee, Uttarakhand, India

International Journal of Engineering Research & Technology (IJERT) 

ISSN: 2278-0181 Vol. 4 Issue 05, May-2015

Click to access role-of-fractal-geometry-in-indian-hindu-temple-architecture-IJERTV4IS050709.pdf

Physical Fractals: Self Similarity and Square-Integratibility

Akhlesh Lakhtakia

Penn State

Speculations in Science and Technology 18, 153-156, 1995

Click to access No260(SST).PDF

The Hindu Temple as a Model of Fractal Cosmology – Forecasting Architecture with Recursive Instruction

Data is Nature

Monday, 6 April 2015

http://www.dataisnature.com/?p=2138

Dancing Architecture: The parallel evolution of Bharatanātyam and South Indian Architecture

Kavitha Jayakrishnan

University of Waterloo
Master of Architecture Thesis 2011

https://uwspace.uwaterloo.ca/bitstream/handle/10012/6356/Jayakrishnan_Kavitha.pdf?sequence=1

Building Science of Indian Temple Architecture

Shweta Vardia

shwetavardia@gmail.com

2008 MS Thesis

Universidade do Minho, Portugal

Click to access 2008_SVardia.pdf

The Fractal Structure of Hindu Temples

Fractal Enlightenment

https://fractalenlightenment.com/14556/fractals/the-fractal-structure-of-hindu-temples

Fractal Geometry And Self-Similarity In Architecture: An Overview Across The Centuries

Nicoletta Sala
Academy o f Architecture o f Mendrisio, University o f Italian Switzerland Largo Bernasconi CH- 6850 Mendrisio
Switzerland
E-mail: nsala @ arch.unisLch

Click to access bridges2003-235.pdf

Shapes, Patterns and Meanings in Indian Temple Architecture

Tanisha Dutta*, V. S. Adane

Department of Architecture and Planning, Visvesvaraya National Institute of Technology Nagpur, India *Corresponding author: ar.tanisha.dd@gmail.com

Received July 17, 2018; Revised August 20, 2018; Accepted November 05, 2018

American Journal of Civil Engineering and Architecture, 2018, Vol. 6, No. 5, 206-215

Available online at http://pubs.sciepub.com/ajcea/6/5/6 ©Science and Education Publishing DOI:10.12691/ajcea-6-5-6

Click to access ajcea-6-5-6.pdf

Hindu Temple: Models of a Fractal Universe. 

Trivedi, K. (1993).

International Seminar on Mayonic Science and Technology,

243-258.

The Visual Computer 5, 243–258 (1989). https://doi.org/10.1007/BF02153753

https://link.springer.com/article/10.1007/BF02153753#citeas

Click to access Hindu_Temple_Models.pdf

Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

IasefMd Riana Jin-HoParka HyungUk Ahna DongkukChangb

aDepartment of Architecture, Inha University, South Korea

bDepartment of Architecture, Chosun University, South Korea

Received 4 May 2006, Revised 21 July 2006, Accepted 15 January 2007, Available online 23 April 2007.

Building and Environment
Volume 42, Issue 12, December 2007, Pages 4093-4107

Click to access 2007_02.pdf

https://www.sciencedirect.com/science/article/abs/pii/S0360132307000273

https://www.semanticscholar.org/paper/Fractal-geometry-as-the-synthesis-of-Hindu-in-Rian-Park/719b6da37091121786525e4b99a667fb098abf49

Symbolism in Hindu Temple
Architecture through Fractal Geoemtry- ‘Thought Behind Form’.

Dutta, T., & V.S.Adane. (2014).

International Journal of Science and Research (IJSR), 489-497.

Click to access U1VCMTQzMjI=.pdf

https://www.semanticscholar.org/paper/Symbolism-in-Hindu-Temple-Architecture-and-Fractal-Dutta-Adane/891db316ae9b06387a0e23ec4e2df649f43d2cd0

Fractal geometry and architecture: some interesting connections

N. Sala

Accademia di Architettura, Università della Svizzera italiana, Mendrisio, Switzerland

Eco-Architecture: Harmonisation between Architecture and Nature 163

Click to access ARC06017FU1.pdf

Temples of Odisha- the Geometry of Plan Form

Rinku Parashar

Assistant Professor Department of Architecture Engineering NIT, Raipur, 492010, India

Dr Abir Bandyopadhyay

Professor & Head Department of Architecture Engineering NIT, Raipur, 492010, India

IJIRST –International Journal for Innovative Research in Science & Technology| Volume 2 | Issue 10 | March 2016 ISSN (online): 2349-6010

Click to access IJIRSTV2I10036.pdf

Shape and geometrical study of fractal cosmology through Orissan Temple architecture

Partha Sarathi Mishra

january 2013

Click to access Shape-and-geometrical-study-of-fractal-cosmology-through-Orissan-Temple-architecture.pdf

“Investigating Architectural Patterns of Indian Traditional Hindu Temples through Visual Analysis Framework,”

Aditya Kumar Singh, Vinay Mohan Das, Yogesh Kumar Garg, Mohammad Arif Kamal ,

Civil Engineering and Architecture, Vol. 10, No. 2, pp. 513-530, 2022.

DOI: 10.13189/cea.2022.100211.

Click to access CEA11-14825255.pdf

https://www.semanticscholar.org/paper/Investigating-Architectural-Patterns-of-Indian-Singh-Das/76b27cc56ba003d899dbc8c0595f304f02e4bb28

“Infinite Sequences in the Constructive Geometry Of Tenth-Century Hindu Temple Superstructures”,

Datta, S.,

School of Architecture and Building Deakin University 1, Gheringhap Street Geelong VIC 3219 AUSTRALIA 

sdatta@deakin.edu.au

Nexus Network Journal – Vol.12, No. 3, 2010 471 – 483

DOI 10.1007/s00004-010-0038-0; published online 15 September 2010
Kim Williams Books, Turin

https://www.semanticscholar.org/paper/Infinite-Sequences-in-the-Constructive-Geometry-Of-Datta/18ed5ec4e6e33a8ebdf5b5c1e6fdc8706b34fdcc

https://link.springer.com/article/10.1007/s00004-010-0038-0

Evolution and Interconnection: Geometry in Early Temple Architecture

DOI:10.1007/978-3-030-57907-4_11

Corpus ID: 238053244

https://www.semanticscholar.org/paper/Evolution-and-Interconnection%3A-Geometry-in-Early-Datta/c767a450532cf281e0bdd0cfac493343c2a2de07

Fractal Geometry as a source of innovative formations in interior design 

Omniah Bahaa Ibrahim

Teaching Assistant, at Faculty of Applied Arts, Interior Design & Furniture Department, Helwan University, Giza, Egypt

DOI: 10.21608/jdsaa.2021.42275.1075

Click to access article_174415_850712616886211291f5a31081befa6e.pdf

Fractal Geometry and Architecture Design: Case Study Review

Xiaoshu Lu1,2, Derek Clements-Croome3, Martti Viljanen1

1Department of Civil and Structural Engineering, School of Engineering, Aalto University, PO Box 12100, FIN-02150, Espoo, Finland
E-mail: xiaoshu@cc.hut.fi
2Finnish Institute of Occupational Health, Finland
3School of Construction Management and Engineering, Whiteknights, University of Reading, PO Box 219, Reading RG6 6AW, UK

Click to access 2_CMSIM_2012_Lu_clements_Croome_viljanen_2_311-322.pdf

A review of the fractal geometry in structural elements

Aman Upadhayay, Dr. Savita Maru
Department of Civil Engineering, Ujjain Engineering College, India

International Journal of Advanced Engineering Research and Science (IJAERS)
Peer-Reviewed Journal
ISSN: 2349-6495(P) | 2456-1908(O)

Vol-8, Issue-7; Jul, 2021
Journal Home Page Available: https://ijaers.com/ 

Article DOI: https://dx.doi.org/10.22161/ijaers.87.3

Click to access 3IJAERS-06202164-Areview.pdf

The fractal analysis of architecture: calibrating the box-counting method using scaling coefficient and grid disposition variables

Michael J Ostwald

School of Architecture and Built Environment, University of Newcastle, University Drive, Callaghan, NSW 2308, Australia;

email: Michael.Ostwald@newcastle.edu.au
Received 15 July 2011; in revised form 21 March 2012

Environment and Planning B: Planning and Design 2013, volume 40, pages 644 – 663 

doi:10.1068/b38124

https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.884.7292&rep=rep1&type=pdf

Mandapa: Its Proportion as a tool in Understanding Indian Temple Architecture

Ragima N Ramachandran

International Journal of Scientific & Engineering Research Volume 10, Issue 7, July-2019 2104 ISSN 2229-5518

Click to access Mandapa-Its-Proportion-as-a-tool-in-Understanding-Indian-Temple-Architecture.pdf

African Fractals

MODERN COMPUTING AND INDIGENOUS DESIGN

RON EGLASH

Book

PARAMETRIZING INDIAN KARNATA-DRAVIDA TEMPLE USING GEOMETRY

SRUSHTI GOUD

BMS School of Architecture, Yelahanka, Bangalore, India

goudsrushti@gmail.com

Click to access ascaad2016_042.pdf

A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

PRATHAMESH GURME1,PROF. UDAY PATIL2

1UG SCHOLAR,2HEAD OF DEPARTMENT, DEPARTMENT OF CIVIL ENGINEERING BHARATI VIDHYAPEETH’S COLLEGE OF ENGINEERING , LAVALE , PUNE , INDIA

INTERNATIONAL JOURNAL FOR RESEARCH & DEVELOPMENT IN TECHNOLOGY

Click to access 2133138-A%20REVIEW%20STUDY%20ON%20ARCHITECTURE%20OF%20HINDU%20TEMPLE.pdf

Exploring Ancient Architectural Designs with Cellular Automata

Hokky Situngkir
[hokky.situngkir@surya.ac.id]
Dept. Computational Sociology, Bandung Fe Institute Center for Complexity Studies in Surya University

BFI Working Paper Series WP-9-2010

Click to access 1508.03610.pdf

WORKING WITH FRACTALS

A RESOURCE FOR PRACTITIONERS OF BIOPHILIC DESIGN

A PROJECT OF THE EUROPEAN ‘COST RESTORE ACTION’ 

PREPARED BY RITA TROMBIN

Click to access Working-with-Fractals-by-Rita-Trombin_v2021-06-21_TBG-COST-RESTORE.pdf

The application of complexity theory and Fractals

in architecture, urban planning and design

Click to access finalCh4.pdf

Chapters

http://www.toofanhaghani.com

The influence of traditional Indian architecture in Balkrishna Doshi’s IIM Complex at Bangalore: A comparative analysis using fractal dimensions and lacunarity

,Mario Lodeweik LIONAR,  (Ph.D. Program of Architecture, Institute of Natural Sciences, Bursa Uludağ University, Bursa, Turkey) 

Özgür Mehmet EDİZ (Department of Architecture, Faculty of Architecture, Bursa Uludağ University, Bursa, Turkey) 

A|Z ITU Mimarlık Fakültesi Dergisi 

DOI: 10.5505/itujfa.2021.80388

https://search.trdizin.gov.tr/yayin/detay/503974/

The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry

Nelly Shafik Ramzy 

Sinai University

Peregrinations: Journal of Medieval Art and Architecture

Volume 5 Issue 2 2015

Click to access 235442558.pdf

PRINCIPLES OF FRACTAL GEOMETRY AND APPLICATIONS IN ARCHITECTURE AND CIVIL ENGINEERING

Anton Vrdoljak, M.Sc.
Faculty of Civil Engineering, University of Mostar, anton.vrdoljak@gf.sum.ba Kristina Miletić, B.Sc.(Math.)
Faculty of Civil Engineering, University of Mostar, kristina.miletic@gf.sum.ba

Number 17, June 2019.

https://hrcak.srce.hr/file/324620

SHAPE AND GEOMETRY OF ORISSAN TEMPLE ARCHITECTURE

Authors: Mishra, Partha Sarathi

MS Thesis, IITR 2012

http://localhost:8081/xmlui/handle/123456789/2017

http://shodhbhagirathi.iitr.ac.in:8081/jspui/handle/123456789/2017

The Shape of Cities: Geometry, Morphology, Complexity and Form

Chapter in book Fractal Cities

Click to access 1370661_Fractal%20Cities%20Chapter%201.pdf

WHOLENESS, VISUAL COMPLEXITY AND MATERIALITY:

A Comparative Analysis Using Fractal Dimension Analysis And Mirror Of The Self-Test In The Case Of Material Imitations.

author | FILIP KINNERT supervisor | doc. PhDr. MARTIN HORÁČEK Ph.D.

Click to access KINNERT-ACAU21-POSTER-211007.pdf


Vastu Purusha Mandala – A human ecological framework for designing living environments.

Venugopal, Jayadevi

In Jetty, C, Chandra, B, Bhashyam, A, & Prabhakara, R (Eds.) Proceedings of International Conference on Advances in Architecture and Civil Engineering (AARCV 2012), Volume 2.
Bonfring, India, pp. 870-877.

Click to access VPM_framework_Jayadevi.pdf

Rediscovering the Hindu Temple:
The Sacred Architecture and Urbanism of India

Vinayak Bharne and Krupali Krusche

Book, ISBN (10): 1-4438-4137-4, ISBN (13): 978-1-4438-4137-5

Click to access 978-1-4438-4137-5-sample.pdf

Borobudur was Built Algorithmically

Hokky Situngkir

[hs@compsoc.bandungfe.net]

Dept. Computational Sociology Bandung Fe Institute

Click to access 2010h.pdf

TEMPLE ARCHITECTURE AND SCULPTURE

NCERT

Click to access kefa106.pdf

Fractal Cities: A Geometry of Form and Function,

Batty, M., Longly, P., 1994, 

Academic Press, San Diego.

Book

Space and Cosmology in the Hindu Temple

Subhash Kak

Presented at Vaastu Kaushal: International Symposium on Science and Technology in Ancient Indian Monuments, New Delhi, November 16-17, 2002.

Click to access Time2.pdf

Gender and space in temple architecture

D. Midhila

midhilachandra@gmail.com

Hindustan Institute of Technology and Sciences, Vijayawada, Andhra Pradesh

Dr. R. V. Nagarajan

rvnagarajan@hindustanuniv.ac.in

Hindustan Institute of Technology and Sciences, Padur, Chennai, Tamilnadu

International Journal of Advance Research, Ideas and Innovations in Technology

2020

Click to access V6I4-1158.pdf

The Role of Five Elements of Nature In Temple Architecture 

Ar. Snigdha Chaudhary

International Journal of Scientific & Engineering Research Volume 8, Issue 7, July-2017 1149 ISSN 2229-5518

Click to access The-Role-of-Five-Elements-of-Nature-In-Temple-Architecture.pdf

Trends in Fractal Dimension in Laxman and Kandariya Mahadev Temples, Khajuraho

Tanisha Dutta1,* and Vinayak S. Adane2

1Phd Research Scholar, Department of Architecture and Planning, Visvesvaraya National Institute of Technology, Nagpur- 440010, India.

2Professor, Department of Architecture and Planning, Visvesvaraya National Institute of Technology, Nagpur- 440010, India. (*Corresponding author)

nternational Journal of Applied Engineering Research ISSN 0973-4562 Volume 13, Number 3 (2018) pp. 1728-1741

© Research India Publications. http://www.ripublication.com

Click to access ijaerv13n3_27.pdf

Hindu Temple Fractals

William J Jackson

https://www.academia.edu/347639/Hindu_Temple_Fractals

Indian Architectural Theory: Contemporary Uses of Vastu Vidya

Vibhuti Chakrabarti

Oxford University Press (1999)

ISBN 0195650417

Maṇḍala in Architecture: Symbolism and Significance for Contemporary Design Education in India

Navin Piplani Ansal University India

Tejwant Singh Brar Ansal University India

IAFOR Journal of Education: Studies in Education

Volume 8 – Issue 4 – 2020

Click to access EJ1279443.pdf

The Intriguing Temples of the 64 Yoginis

2022

The intriguing temples of the 64 Yoginis