Charles Sanders Peirce’s Visual Logic: Diagrams and Existential Graphs

Source: Toward an Integrated History and Philosophy of Diagrammatic Practices

Source:

Source: PEIRCE’S CONTINUUM: A METHODOLOGICAL AND MATHEMATICAL APPROACH
Key Terms
- Diagrams
- Existential graphs
- Conceptual graphs
- Aristotle
- Euclid
- George Boole (1854)
- Gottlob Frege (1879)
- Charles Sanders Peirce
- Giuseppe Peano (1889)
- Semantic Networks
- Triadic logic
- Multivalent logic
- Bivalent Logic
- Trivalent Logic
- Induction, Deduction, Abduction
- Alpha, Beta, Gamma Graphs
- Logical Graphs
- Logicality
- Diagrammatic Logic
- Diagrammatology
- Euler Diagrams
- Venn Diagrams
- Sets and Tables
- Knots and Nets
- Logic
- Diagrams
- Peirce
- Alpha Graphs
- Propositional Logic
- Multi-Model Reasoning
- Symbolic Logic
- Modal Logic
- History of Logic
- Boolean Algebra (B)
- Kripke Semantics
- Peirce Algebras
- Algebraic Logic
- Relation Algebras (R)
- Logics of Programs
- Knowledge Representation
- Set and Relations
- Peirce’s Logic of Relatives
- First Order Logic
- Discursive Reasoning
- Diagrammatic Reasoning
- Sets, Supersets, Subsets
- Set Theory
- Cognitive Maps
- Mental Models
- Higraphs
- George Boole’s Algebra of Logic
- Augustus De Morgan’s Logic of Relations
- John Venn
- Sheet of Assertion
- Predicate Calculus
- Heterogeneous Logic
- Graphs, Diagrams, Maps, Networks, Frames
- Monadic, Dyadic, Triadic
- Firstness, Secondness, Thirdness
- Speech Act Logic
- Temporal Logic
- First Order Predicate Logic
- Second Order Predicate Logic
- Formal (Deductive) Logic
- Peirce’s Continuum
- Hyperproof Software
- String Diagrams Calculus
Key Scholars
- John F. Sowa
- Priscila Lena Farias
- Joao Queiroz
- Frederik Stjernfelt
- L H Kauffman
- Ahti-Veikko Pietarinen
- Sun-Joo Shin
- Francesco Bellucci
- Silvia De Toffoli
- Eric Morgan Hammer
Visual Logic Diagrams
- Existential Graphs
- Euler Diagrams
- Venn Diagrams
- Hasse Diagrams
- Marlo Diagrams
- Knots Diagrams
- Feynman Diagrams
- Carroll Diagrams
- Euclidean Diagrams
- Commutative Diagrams
- Spider Diagrams
- String Diagrams
Source: WHO’S AFRAID OF MATHEMATICAL DIAGRAMS?

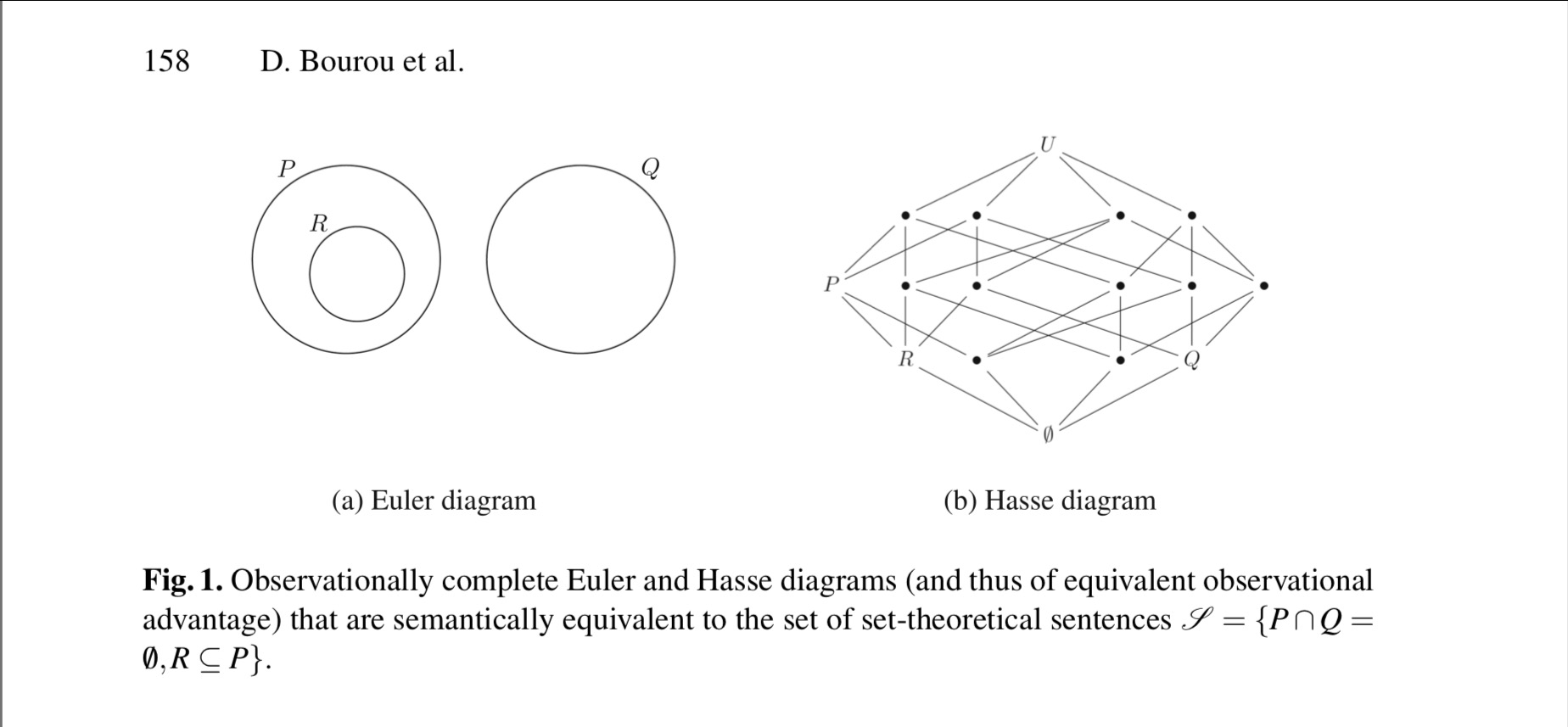
Source: Euler vs Hasse Diagrams for Reasoning About Sets: A Cognitive Approach
Source: WHAT ARE MATHEMATICAL DIAGRAMS?

Source: WHAT ARE MATHEMATICAL DIAGRAMS?

Source: Peirce’s Tutorial on Existential Graphs

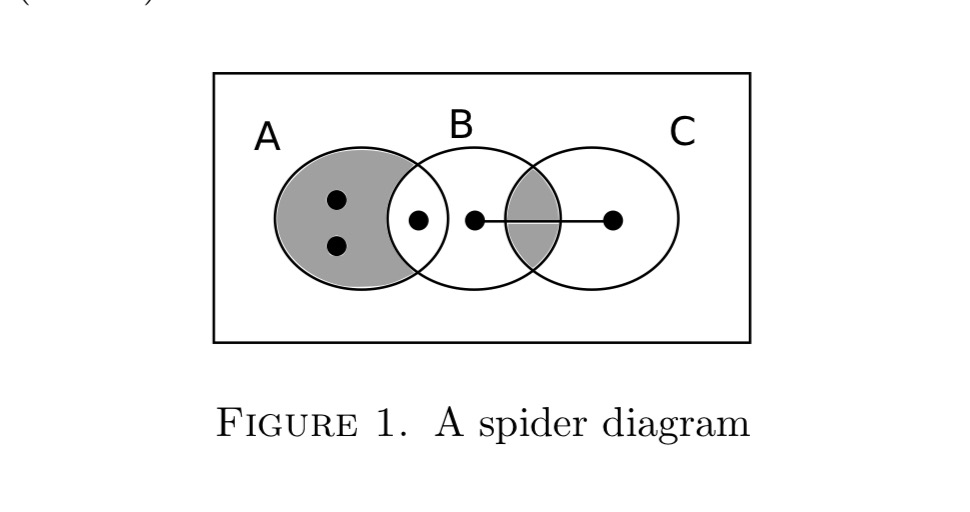
Source: The Semiotics of Spider Diagrams
Source: The Semiotics of Spider Diagrams

Source: Introduction: Diagrammatical reasoning and Peircean logic representations

Source: Introduction: Diagrammatical reasoning and Peircean logic representations

Source: Introduction: Diagrammatical reasoning and Peircean logic representations

Source: Introduction: Diagrammatical reasoning and Peircean logic representations

Source: General Introduction to Logic of the Future

Source: Challenges and Opportunities for Existential Graphs

Source: Peirce on Logical Diagrams

Source: Peirce, logic diagrams, and the elementary operations of reasoning

Source: Peirce, logic diagrams, and the elementary operations of reasoning

Source: Peirce, logic diagrams, and the elementary operations of reasoning

Alpha, Beta, and Gamma Graphs
Source:

Source:

Source:

Source:

Source: The Logic of Peirce Algebras
Algebras of the form ( B, R, : ) were introduced by Brink (1981) as Boolean modules. Sources for Peirce algebras are Brink, Britz and Schmidt (1994) and Schmidt (1993).
Unlike the one-sorted language of relation algebras, the algebraic language of Peirce algebras has two sorts of terms: one interpreted in B, the other in R. Terms of the first sort are called set terms, terms of the second sort relation terms. Identities between set terms are called set identities; identities between relation terms are relation identities.
Brink et al. (1994) link Peirce algebras to dynamic algebras. Like Peirce algebras these are two-sorted algebras of sets and relations, but their relations are organized in a Kleene algebra, not in a relation algebra. It may be shown that any join-complete Peirce algebra gives rise to a dynamic algebra.
Another class of algebras closely related to Peirce algebras, is the class of extended relation algebras studied by Suppes (1976). Roughly, these are term- definably equivalent with Peirce algebras in which the sortal distinctions have been dropped.
Source: A diagrammatic reasoning system for the description logic ALC
Diagrammatic reasoning is a tradition of visual logic that allows sentences that are equivalent to first order logic to be written in a visual or structural form: usually for improved usability. A calculus for the diagram can then be defined that allows well-formed formulas to be derived. This calculus is intended in the analog of logical inference. Description logics (DLs) have become a popular knowledge representation and processing language. DLs correspond to decidable fragments of first order logic; their notation is in the style of symbolic, variable-free formulas. Moreover, DLs are equipped with table au theorem provers that are proven to be sound and complete. Although DLs have roots in diagrammatic languages (such as semantic networks), they are elaborated in a purely symbolic manner. This paper discusses how DLs can be equivalently represented in terms of a diagrammatic reasoning system. First, existing diagrammatic reasoning systems, namely spider- and constraint diagrams, as well as existential and conceptual graphs, are investigated to determine if they are compatible with DLs. It turns out that Peirce’s existential graphs are better suited for this purpose than the alternatives we examine. The paper then redevelops the DL ALC, which is the smallest propositional DL, by means of labeled trees, and provides a diagrammatic representation for these trees in the style of Peircean graphs. We provide a calculus based on C.S. Peirce’s calculus for existential graphs and prove the soundness and completeness of the calculus. The calculus acts on labeled trees, but can be best understood as a diagrammatic calculus whose rules modify the Peircean-style representation of ALC.
Source: Derik Hawley / Logic in Pictures
Just as “discursive” reasoning has been given formal analysis through the methods of formal logic and formal language theory, graph theory provides a framework by means of which “diagrammatic” reasoning can be given such a formal treatment. Just as formal logic replaces words with abstract symbols, Graph theory replaces icons and arrows in a diagram with abstract entities called vertices and arcs. This allows the formal properties of the symbolism to be examined without the intervention of any aspects of the conception which is conveyed by the symbol affecting the inference. Formal logic treats inference as a set of operations that deal only with the operations on the symbols themselves, and does not examine the inference that involves associations based upon the conceptions conveyed by the symbols. There are certain advantages to such a treatment. Formal logic provides a framework where the examination of the validity of an argument can be examined without the intervening effects of connotations and emotions. The formal examination results in a knowledge of whether or not the premises of an argument are sufficient evidence for the conclusion. This is a useful thing for it provides us with a method of examining our own opinions and those of others.
The study of logic has, with one exception, dealt only with “discursive” symbolisms. It has examined the ways in which the discursive symbolisms can be formalized using different systems. Historically, one can divide the set of logic systems into three categories. First there is the Aristotelian Logic system, secondly there are propositional systems and finally there are the modern quantified, relational logics (which include first and second order logic). Each of these developments attempts to improve the range of arguments that can be given formal treatment. However, there has never been an attempt to deal with “diagrammatic symbols” and provide a framework for the examination of the sorts of inferences that involve the formal aspects of diagrammatic symbols. By using graph theory we can examine diagrammatic symbolisms in a manner such that they can undergo the same formal scrutiny that discursive reasoning can be given in formal logic.
In this chapter I will be giving an introduction to graph theory and a few examples of the manner in which graph theory can be applied to diagrammatic reasoning. I will then sketch a method by which Peirce’s existential graphs can be translated into graph theory.
Source: Diagrams 2018
Diagrams 2018 Accepted Tutorials
Diagrams 2018 has six scheduled tutorials (subject to change):
Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning
Presenters: Aleks Kissinger and Bob Coecke
Time: 09:00 – 10:30Description: We provide a self-contained introduction to quantum theory using a unique diagrammatic language. Far from simple visual aids, the diagrams we use are mathematical objects in their own right, which allow us to develop from first principles a completely rigorous treatment of ‘textbook’ quantum theory. Additionally, the diagrammatic treatment eliminates the need for the typical prerequisites of a standard course on the subject, making it suitable for a multi-disciplinary audience with no prior knowledge in physics or advanced mathematics.
By subscribing to a diagrammatic treatment of quantum theory we place emphasis on quantum processes, rather than individual systems, and study how uniquely quantum features arise as processes compose and interact across time and space. We introduce the notion of a process theory, and from this develop the notions of pure and mixed quantum maps, measurements and classical data, quantum teleportation and cryptography, models of quantum computation, quantum algorithms, and quantum non-locality. The primary mode of calculation in this tutorial is diagram transformations, where simple local identities on diagrams are used to explain and derive the behaviour of many kinds of quantum processes.
This tutorial roughly follows a new textbook published by Cambridge University Press in 2017 with the same title.
Diagrams in Kant’s Philosophy of Mathematics: Image and Intuition
Presenter: Ofra Rechter
Time: 11:00 – 12:30Description: Kant’s notion of an image (Bild) is at play in the examples of mathematical construction from both geometry and arithmetic that are considered in the Critique of Pure Reason. Pre-Critical texts distinguish linguistic signs from mathematical sensible means for cognition, geometrical figures and signs in numeral systems, but the Critical philosophy raises the question of what the operation signs signify. In this tutorial we articulate the
central problems about Kant’s epistemology of mathematics from the vantage point of the problematic of pure intuition as an intuition of images that instantiate mathematical concepts. Our point of departure is that a phenomenological aspect of the use made of geometrical figures in mathematical reasoning in Kant also underpins the role of numeral types in the construction of the elementary arithmetic. But, the manipulation of images in calculation or arithmetical reasoning cannot simply be a geometry of numerical signs for Kant. An attractive proposal by Michael Friedman associates the mathematical operations with what Kant calls schemata (and, thereby, via the imagination, both with time and space– the forms of sensibility, and with the intellectual synthesis under the categories). This seems to work quite neatly when the operations in question are only Euclidean postulates. Can the proposal be extended to arithmetic? to address this question we will isolate a problem that is distinctive of Kant’s philosophy of arithmetic: an inherent ambiguity in his account between successive addition as a species of synthesis and the primitive recursive binary operation of addition. By showing that the appeal to images serves Kant in bridging this ambiguity, the epistemological and the ontological accounts of a mathematical object of intuition are distinguished. Finally, time permitting, we will indicate how this result also contributes to resolving a dispute over mathematical intuition and the Kantian roots of Finitism between Charles Parsons and William Tait.Carroll diagrams: design and manipulation
Presenter: Amirouche Moktefi
Time: 14:00 – 15:30Description: The use of diagrams in logic is old. Euler and Venn schemes are among the most popular. Carroll diagrams are less known but are occasionally mentioned in recent literature. The objective of this tutorial is to expose the working of Carrol’s diagrams and their significance from a triple perspective: historical, mathematical and philosophical. The diagrams are exposed, worked out and compared to Euler-Venn diagrams. These schemes are used to solve the problem of elimination which was widely addressed by early mathematical logicians in Boole’s footsteps. Logicians worked on a general method for finding the conclusion that is to be drawn from any number of premises containing any number of terms. For this purpose, they designed symbolic, visual and mechanical devices. The significance of Venn and Carroll diagrams is better understood within this historical context. The development of logic notably created the need for complex diagrams to represent n terms, rather than merely 3. Several methods to construct diagrams for n terms, with different strategies, are discussed. Finally, the philosophical significance of Carroll diagrams is discussed in relation to the use of transfer rules. This practice is connected to recent philosophical debates on the role of diagrams in mathematical practice.
Were “super-turing” diagrammatic reasoning competences ancient products of biological evolution?
Presenter: Aaron Sloman
Time: 14:00 – 15:30Description: I’ll give a highly interactive introduction to aspects of the Turing-inspired Meta-Morphogenesis project, focusing on conjectures about evolutionary processes leading to the amazing discoveries in topology and geometry by ancient mathematicians, and corresponding competences of young humans and other intelligent animals, suggesting brain processes very different from anything currently understood in AI or neuroscience. A conjectured “super-turing membrane machine” will be sketched along with requirements for further development. Whether this can be implemented as a virtual machine running on digital computing machinery is not yet clear. The tutorial will be highly interactive with many different examples discussed in detail, depending on interests of participants, e.g. examples of reasoning about affordances, using “diagrams in the mind”. More details can be found here.
Using verbal protocols to support diagram design
Presenter: Thora Tenbrink
Time: 16:00 – 17:30Description: How do we know what people perceive in a diagram? A diagram can be an excellent medium for communication of complex facts and relationships. Users may be able to learn a lot just from a quick glance at a well-designed diagram. Unfortunately, what users take from a diagram may not always be the same as what its designers intended to communicate. This can have enormous consequences, ranging from misinterpretation of research outputs to false representation in the media, to the point of misguided policy decisions coming from miscommunication of central research insights.
In this tutorial, we will look at the use of verbal protocols as a tool in diagram design. The way people talk about a diagram can reveal a lot about how they understand it, what they misinterpret, and what kinds of design features could be amended to enhance clarity, ensuring successful communication.
The tutorial will start by looking at the kinds of problems that frequently arise in diagram interpretation, such as cognitive biases, misinterpretations, and effects of lack of expertise. Following a brief discussion of the value of verbal protocols in this area, we will turn to the practical aspects of verbal protocol data collection, analysis, and interpretation.
Peirce on Diagrammatic Reasoning and Semeiotic
Presenters: Javier Legris and Cassiano Rodrigues
Time: 16:00 – 17:30Description: Charles Sanders Peirce (1839-1914) is one of the “grounding fathers” of mathematical logic, having developed all of the key formal results of modern logic. Starting from Boole’s algebra of logic and De Morgan’s logic of relations, Peirce developed his own system of quantifiers and relative predicates. Due to philosophical reasons, he became dissatisfied with algebraic notation for logic, developing a diagrammatic logical system of Existential Graphs. Regarding it as his masterpiece in logic, Peirce called it the logic of the future. For Peirce, all necessary reasoning is diagrammatic. Generalizing, we can say all logical inferences can be interpreted as diagrammatic experimentations upon signs. This is why Peirce thinks of logic as “semeiotic”, a general and “quasi-necessary” doctrine of signs inquiring into their active role as conveyers of meaning.
The tutorial will present Peirce’s logic and philosophy of logic, focusing more on the arguments supporting some of Peirce’s most original ideas. His distinction between logic and mathematics will be hinted at, aiming at showing why creativity and discovery have an important place in Peirce’s thought.
Specific topics: Relatives, illation, and semeiotic; quantifiers; existential graphs; theorematic and corollarial deductions; Peirce’s refusal of logicism; Notes on bibliography and current research.
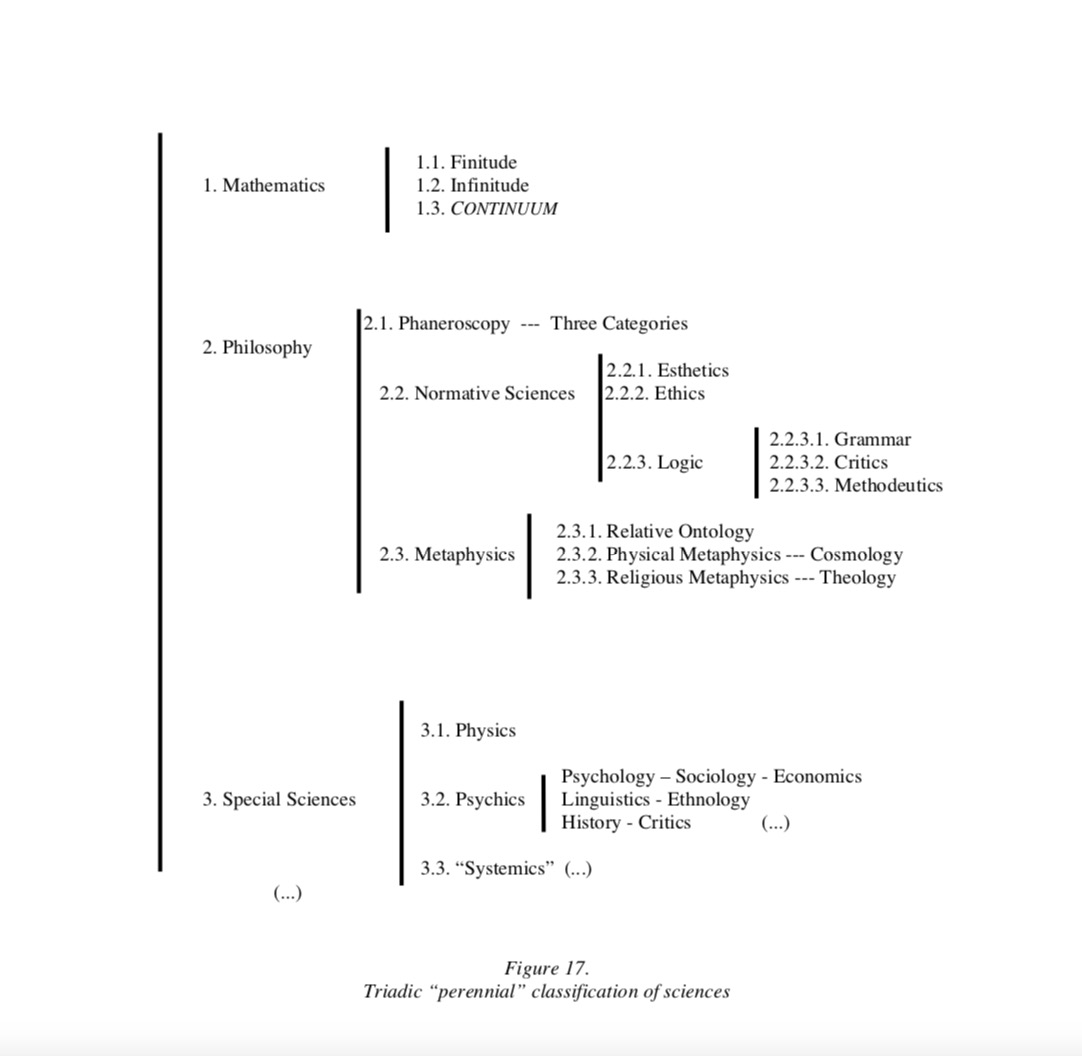
Source: PEIRCE’S CONTINUUM: A METHODOLOGICAL AND MATHEMATICAL APPROACH

Source:

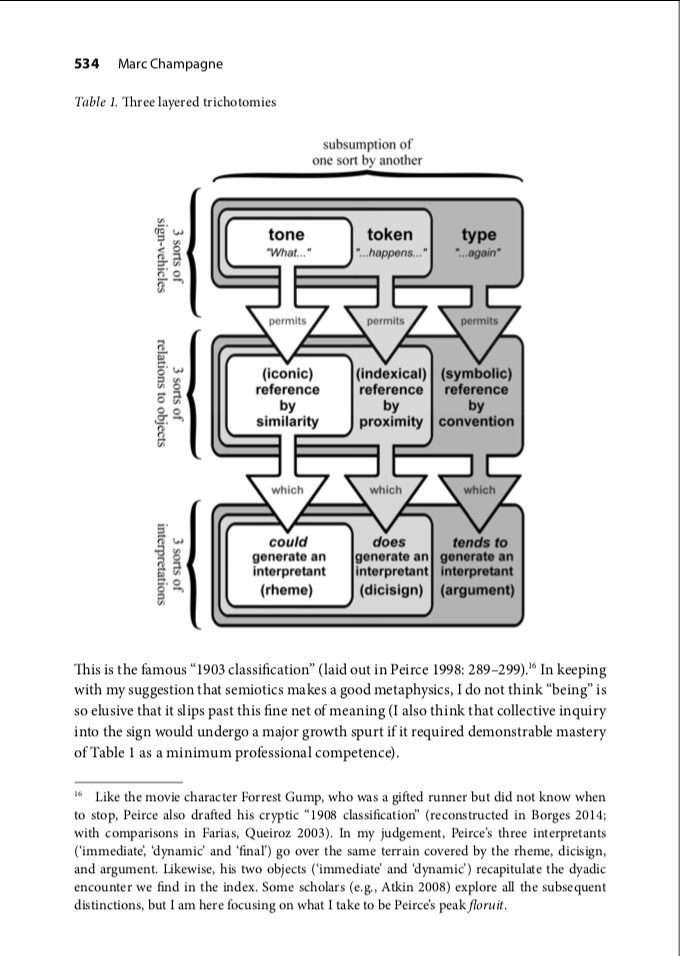
Source: A less simplistic metaphysics: Peirce’s layered theory of meaning as a layered theory of being
Source: PEIRCE’S CONTINUUM: A METHODOLOGICAL AND MATHEMATICAL APPROACH

Source: Interdisciplinary Aspects of Cognition
Computation: From Mathematics to Computer Science
Hofstadter’s 800-page bestseller [25] aims to show how self-reference, which essentially corresponds to the mathematical notion of recursion, is the basis of self-awareness. Hofstadter considers the diagonal argument used by Kurt Godel to prove his two incompleteness theorems: the use of a property that refer to itself to prove that (1) there is no axiomatic system capable to prove all properties of the arithmetic and (2) no consistent axiomatic system which includes Peano arithmetic can prove its own consistency.
G ̈odel’s results may be seen as an evidence that there is no objective reality and that there are questions that cannot have an answer. Hofstadter writes in the preface to the 20th-anniversary edition of his book: ‘Something very strange thus emerges from the G ̈odelian loop: the revelation of the causal power of meaning in a rule-bound but meaning-free universe. […] When and only when such a loop arises in a brain or in any other substrate, is a person — a unique new “I” — brought into being.’ This means that symbolic computation, especially through recursion, potentially allows meaning to emerge from the manipulation of meaningless symbols, up to the complexity of human reasoning. The fact that recursion is the fundamental mathematical tool in mechanising reasoning is not a surprise for a computer scientist. After all, programming languages used in artificial intelligence, either Lisp-like functional languages or Prolog-like declarative languages, heavily exploit recursion.
My Related Posts
Knot Theory and Recursion: Louis H. Kauffman
Semiotic Self and Dialogic Self
Paradoxes, Contradictions, and Dialectics in Organizations
Reflexivity, Recursion, and Self Reference
Narrative Psychology: Language, Meaning, and Self
System Archetypes: Stories that Repeat
From Systems to Complex Systems
Micro Motives, Macro Behavior: Agent Based Modeling in Economics
Gantt Chart Simulation for Stock Flow Consistent Production Schedules
Production and Distribution Planning : Strategic, Global, and Integrated
Portfolio Planning Models for Corporate Strategic Planning
What are Problem Structuring Methods?
Measuring Globalization: Global Multi Region Input Output Data Bases (G-MRIO)
Stock Flow Consistent Input Output Models (SFCIO)
Stock-Flow Consistent Modeling
Stock Flow Consistent Models for Ecological Economics
Global Flow of Funds: Statistical Data Matrix across National Boundaries
Phillips Machine: Hydraulic Flows and Macroeconomics
Foundations of Balance Sheet Economics
Contagion in Financial (Balance sheets) Networks
Balance Sheets, Financial Interconnectedness, and Financial Stability – G20 Data Gaps Initiative
Credit Chains and Production Networks
Supply Chain Finance (SCF) / Financial Supply Chain Management (F-SCM)
Network Economics of Block Chain and Distributed Ledger Technology
Currency Credit Networks of International Banks
Intra Industry Trade and International Production and Distribution Networks
Systems Biology: Biological Networks, Network Motifs, Switches and Oscillators
Global Financial Safety Net: Regional Reserve Pools and Currency Swap Networks of Central Banks
Evolving Networks of Regional RTGS Payment and Settlement Systems
Structure and Evolution of EFT Payment Networks in the USA, India, and China
Hierarchy Theory in Biology, Ecology and Evolution
Key Sources of Research
Natural logic is diagrammatic reasoning about mental models
John F.Sowa
Kyndi Inc, San Mateo, CA
Available online 15 April 2020, Version of Record 15 April 2020.
Procedia Computer Science
Volume 169, 2020, Pages 31-45
Sheets, Diagrams, and Realism in Peirce
By Frederik Stjernfelt
Semiotics, Schemata, Diagrams, and Graphs: A New Form of Diagrammatic Kantism by Peirce
CLAUDIO PAOLUCCI
Graphs as Images vs. Graphs as Diagrams: A Problem at the Intersection of Semiotics and Didactics
MICHAEL MAY
Two Dogmas of Diagrammatic Reasoning: A View from Existential Graphs
AHTI-VEIKKO PIETARINEN AND FRANCESCO BELLUCCI
Peirce on Perception and Reasoning
From Icons to Logic
Edited by
Kathleen A. Hull and Richard Kenneth Atkins
Routledge Studics in American Philosophy
2017
ISBN: 978-1-138-21501-6 (hbk)
ISBN: 978-1-315-44464-2 (ebk)
From Existential Graphs to Conceptual Graphs
John F. Sowa
VivoMind Research, LLC
The Philosophical Psychology of Charles S. Peirce
Claudia Cristalli
UCL PhD Thesis
Interdisciplinary Aspects of Cognition
Antonio Cerone1,4, Siamac Fazli1, Kathy L. Malone2, and Ahti-Veikko Pietarinen3,4
1 Department of Computer Science, Nazarbayev University, Nur-Sultan, Kazakhstan
{antonio.cerone,siamac.fazli}@nu.edu.kz
2 Graduate School of Education, Nazarbayev University, Nur-Sultan, Kazakhstan
kathy.malone@nu.edu.kz
3 Department of History, Philosophy and Religious Studies, Nazarbayev University, Nur-Sultan, Kazakhstan
ahtiveikko.pietarinen@nu.edu.kz
4 Intelligence, Robotics and Cognition Cluster, Nazarbayev University, Nur-Sultan, Kazakhstan
Diagrams 2021
2021. Diagrammatic Representation and Inference: 12th International Conference,
Virtual, September 28–30, 2021, Proceedings. Springer-Verlag, Berlin, Heidelberg.
https://dl.acm.org/doi/proceedings/10.1007/978-3-030-86062-2
The Beauty of Graphs
- January 2018
DOI:10.1007/978-3-319-91376-6_2
- In book: Diagrammatic Representation and Inference (pp.9-12)
Ahti-Veikko Pietarinen 1,2
1Tallinn University of Technology, Tallinn, Estonia
ahti-veikko.pietarinen@ttu.ee
2Nazarbayev University, Astana, Kazakhstan
https://www.researchgate.net/publication/325185161_The_Beauty_of_Graphs
General Introduction to Logic of the Future
Pietarinen, Ahti-Veikko.
Volume 2 The 1903 Lowell Lectures, edited by Ahti-Veikko Pietarinen, Berlin, Boston: De Gruyter, 2021, pp. 1-14.
https://doi.org/10.1515/9783110740462-001
https://www.degruyter.com/document/doi/10.1515/9783110740462-001/pdf
Why Images Cannot be Arguments, But Moving Ones Might
Marc Champagne1 · Ahti‐Veikko Pietarinen2
Argumentation 2019
https://doi.org/10.1007/s10503-019-09484-0
IDEAS IN ACTION
PROCEEDINGS OF THE APPLYING PEIRCE CONFERENCE
Nordic Studies in Pragmatism 1
Edited by
Mats Bergman,
Sami Paavola, Ahti-Veikko Pietarinen & Henrik Rydenfelt
Nordic Pragmatism Network, Helsinki 2010
Challenges and Opportunities for Existential Graphs
Ahti-Veikko Pietarinen
University of Helsinki 2010
Page 288, Previous Reference
Peirce’s Diagrammatic Logic and the Opposition between Logic as Calculus vs. Logic as Universal Language
Legris Javier
Revista Portuguesa de Filosofia 73 (3-4):1095-1114 (2017)
DOI 10.17990/RPF/2017_73_3_1095.
https://www.publicacoesfacfil.pt/product.php?id_product=1058
The Logic of Peirce Algebras
MAARTEN DE RIJKE
Department of Software Technology, CW1,P.O. Box 94079, 1090 GB Amsterdam, The Netherlands
Email: mdr@cwi.nl
Journal of Logic, Language, and Information 4: 227-250, 1995.
Peirce’s Diagrammatic Solutions to ‘Peirce’s Puzzle’
Ahti-Veikko Pietarinen
Diagrammatic Representation and Inference: 12th International Conference, Diagrams 2021, Virtual, September 28–30, 2021,
Proceedings Sep 2021 Pages 246–250
https://doi.org/10.1007/978-3-030-86062-2_23
https://dl.acm.org/doi/10.1007/978-3-030-86062-2_23
A diagrammatic reasoning system for the description logic ALC
Journal of Visual Languages and Computing
Volume 19 Issue 5 October, 2008 pp 539–573
https://doi.org/10.1016/j.jvlc.2007.12.003
https://dl.acm.org/doi/10.1016/j.jvlc.2007.12.003
Two papers on existential graphs by Charles Peirce
Ahti-Veikko Pietarinen
2014
Synthese
DOI 10.1007/s11229-014-0498-y
ON THE SUPREME BEAUTY OF LOGICAL GRAPHS
AHTI-VEIKKO PIETARINEN
Cuadernos de Sistemática Peirceana 8
2016
Peirce and diagrams: two contributors to an actual discussion review each other
Ahti-Veikko Pietarinen
Frederik Stjernfelt
Synthese
DOI 10.1007/s11229-015-0658-8
https://www.academia.edu/17249725/Peirce_and_Diagrams?from=cover_page
Peirce’s Dragon Logic of 1901.
Ma, M., Pietarinen, A.-V.:
Preprint (2019)
Chapter 1
Mutual Insights on Peirce and Husserl
Ahti-Veikko Pietarinen, Mohammad Shafiei and Frederik Stjernfelt
Diagrammatic reasoning. Some notes on Charles S. Peirce and Friedrich A. Lange.
Bellucci, F. (2013).
History and Philosophy of Logic 34(4), 293-305.
DOI: 10.1080/01445340.2013.777991
https://www.tandfonline.com/doi/abs/10.1080/01445340.2013.777991
Logische Studien: Ein Beitrag Zur Neubegrundung Der Formalen Logik Und Der Erkenntnisstheorie.
Lange, F. A. (1877).
Iserlohn: J. Baedeker.
Logic of the Future: Writings on Existential Graphs.
Peirce, C. S. (2019-).
Ed. By A.-V. Pietarinen,
Peirceana Vols.1-3. Mouton De Gruyter.
Peirce and Diagrams: Peirce and Husserl in Professor Stjernfelt’s Diagrammatology.
Pietarinen, A.-V. (2015).
Synthese 192, 1073-1088. 10.1007/s11229-015-0658-8
Is there a General Diagram Concept?
Pietarinen, A.-V. (2016).
In Krämer, S. & C. Ljundberg (eds.), Thinking in Diagrams: The Semiotic Basis of Human Cognition,
Berlin: Mouton de Gruyter, 121-138.
The Existential Graphs of Charles S. Peirce.
Roberts, D. D. (1973).
The Hague: Mouton.
Diagrammatology. An investigation on the borderlines of phenomenology, ontology, and semiotics.
Stjernfelt, F. (2007).
Synthese Library 336. Dordrecht: Springer.
An Examination of Diagrammatic Representations, Graph Theory and Logic
Derik Hawley
MA Thesis
University of Waterloo
Waterloo, Ontario, Canada, 1994
Existential Graphs: What a Diagrammatic Logic of Cognition Might Look Like
Ahti-Veikko Pietarinen
History and Philosophy of Logic
Volume 32, 2011 – Issue 3 Pages 265-281
https://doi.org/10.1080/01445340.2011.555506
https://www.tandfonline.com/doi/abs/10.1080/01445340.2011.555506
EXISTENTIAL GRAPHS AS AN INSTRUMENT OF LOGICAL ANALYSIS: PART I. ALPHA.
BELLUCCI, F., & PIETARINEN, A. (2016).
The Review of Symbolic Logic, 9(2), 209-237.
doi:10.1017/S1755020315000362
Peirce’s Contributions to Possible-Worlds Semantics.
Pietarinen, AV.
Stud Logica 82, 345–369 (2006).
https://doi.org/10.1007/s11225-006-8102-1
https://link.springer.com/article/10.1007/s11225-006-8102-1
Peirce and the logical status of diagrams,
Sun-joo Shin (1994)
History and Philosophy of Logic, 15:1, 45-68,
DOI: 10.1080/01445349408837224
https://www.tandfonline.com/doi/abs/10.1080/01445349408837224
Martin Gardner. Logic machines and diagrams.
Mays, W. (1959).
McGraw-Hill Book Company, Inc., New York-Toronto-London 1958, ix 157 pp. Journal of Symbolic Logic, 24(1), 78-79. doi:10.2307/2964627
Euler’s visual logic
Eric Hammer & Sun-Joo Shin (1998)
History and Philosophy of Logic, 19:1, 1-29, DOI: 10.1080/01445349808837293
https://www.tandfonline.com/doi/abs/10.1080/01445349808837293
“Peirce on Logical Diagrams.”
Hammer, Eric.
Transactions of the Charles S. Peirce Society 31, no. 4 (1995): 807–27. http://www.jstor.org/stable/40320573.
The Iconic Logic of Peirce’s Graphs
by Sun-Joo Shin
Cambridge, MA : MIT Press, 2002. x + 208.
“What is a Logical Diagram?”
Catherine Legg
Diagrams
First published Tue Aug 28, 2001; substantive revision Thu Dec 13, 2018
Stanford Encyclopedia of Philosophy
https://plato.stanford.edu/entries/diagrams/
Diagrams 2018
Diagrammatic Representation and Inference
10th International Conference, Diagrams 2018, Edinburgh, UK, June 18-22, 2018, Proceedings
https://link.springer.com/book/10.1007/978-3-319-91376-6
http://www.diagrams-conference.org/2018/index.html%3Fp=320.html
SetVR 2020
International Workshop on Set Visualization and Reasoning
August 2020, Tallinn, Estonia
(co-located with Diagrams 2020)
https://sites.google.com/site/setvr2kn/current-workshop
DIAGRAMS 2020
11th International Conference on the Theory and Application of Diagrams, 24-28 August 2020
Home
http://link.springer.com/openurl.asp?genre=issue&issn=0302-9743&volume=12169
Diagrams 2022
Diagrammatic Representation and Inference
13th International Conference, Diagrams 2022, Rome, Italy, September 14–16, 2022, Proceedings
https://link.springer.com/book/10.1007/978-3-031-15146-0
Home
Existential Graphs
MS 514 by Charles Sanders Peirce
with commentary by John F. Sowa
http://www.jfsowa.com/peirce/ms514.htm
A Survey of Venn Diagrams
Frank Ruskey and Mark Weston
Department of Computer Science
University of Victoria
Victoria, B.C. V8W 3P6
CANADA
https://www.combinatorics.org/files/Surveys/ds5/VennEJC.html
THE WORK OF EDWARD TUFTE AND GRAPHICS PRESS
GRAPHICS PRESS LLC P.O. BOX 430 CHESHIRE, CT 06410 800 822-2454
https://www.edwardtufte.com/tufte/
Forms and Roles of Diagrams in Knot Theory
Silvia De Toffoli • Valeria Giardino
Erkenn (2014) 79:829–842
DOI 10.1007/s10670-013-9568-7
WHAT ARE MATHEMATICAL DIAGRAMS?
Silvia De Toffoli
Forthcoming in Synthese
The Aesthetics of Science: Beauty, Imagination and Understanding
edited by Milena Ivanova, Steven French
How Do Feynman Diagrams Work?.
James Robert Brown;
Perspectives on Science 2018; 26 (4): 423–442.
doi: https://doi.org/10.1162/posc_a_00281
https://direct.mit.edu/posc/article/26/4/423/15455/How-Do-Feynman-Diagrams-Work
Feynman Diagrams: Modeling between Physics and Mathematics.
Michael Stöltzner;
Perspectives on Science 2018; 26 (4): 482–500.
doi: https://doi.org/10.1162/posc_a_00284
Feynman diagrams
From complexity to simplicity and back
Robert Harlander
R. Harlander
TTK, RWTH Aachen University
Tel.: +49-241-80-27045
Fax: +49-241-80-22187
E-mail: harlander@physik.rwth-aachen.de
From Euclidean geometry to knots and nets
Synthese volume 196, pages 2715–2736 (2019)
https://link.springer.com/article/10.1007/s11229-017-1558-x
WHO’S AFRAID OF MATHEMATICAL DIAGRAMS?
Silvia De Toffoli
Penultimate version (21 January 2022) // Forthcoming in Philosophers’ Imprint
‘CHASING’ THE DIAGRAM—THE USE OF VISUALIZATIONS IN ALGEBRAIC REASONING
SILVIA DE TOFFOLI
Department of Philosophy, Stanford University
450 SERRA MALL, STANFORD CA 94305, USA
E-mail: silviadt@stanford.edu
THE REVIEW OF SYMBOLIC LOGIC Volume 10, Number 1, March 2017
Aligning logical and psychological perspectives on Diagrammatic Reasoning
Keith Stenning
Human Communication Research Centre Edinburgh University
Oliver Lemon
Dept of Computer Science Manchester University
https://web-archive.southampton.ac.uk/cogprints.org/820/2/lemon.ps
The forgotten individual: diagrammatic reasoning in mathematics.
Shin, SJ.
Synthese 186, 149–168 (2012).
https://doi.org/10.1007/s11229-012-0075-1
https://link.springer.com/article/10.1007/s11229-012-0075-1
“Introduction: Diagrammatical reasoning and Peircean logic representations”
Queiroz, João and Stjernfelt, Frederik.
Semiotica vol. 2011, no. 186, 2011, pp. 1-4.
https://doi.org/10.1515/semi.2011.043
https://www.degruyter.com/document/doi/10.1515/semi.2011.043/html#Chicago
https://philarchive.org/archive/QUEIDR
Images, diagrams, and narratives: Charles S. Peirce’s epistemological theory of mental diagrams
Markus Arnold
Semiotica vol. 2011, no. 186, 2011, pp. 5-20.
https://doi.org/10.1515/semi.2011.044
https://www.degruyter.com/document/doi/10.1515/semi.2011.044/html
Peirce’s Graphs—The Continuity Interpretation.
Zeman, J. J. (1968).
Transactions of the Charles S. Peirce Society, 4(3), 144–154. http://www.jstor.org/stable/40319551
Peirce, logic diagrams, and the elementary operations of reasoning
P. N. Johnson-Laird
Department of Psychology, Princeton University, Princeton, NJ 08540, USA Email: phil@princeton.edu
THINKING AND REASONING, 2002, 8(1), 69–95
DOI: 10.1080/13546780143000099
Click to access 2002peirce.pdf
One, two, three . . . continuity: C.S. Peirce and the nature of the continuum
Author: Robertson, R.
Source: Cybernetics & Human Knowing, Volume 8, Numbers 1-2, 1 January 2001, pp. 7-24(18)
https://www.ingentaconnect.com/content/imp/chk/2001/00000008/f0020001/74
Peirce and Spencer-Brown: history and synergies in cybersemiotics
L.H, Kauffman & Brier, Søren. (2001).
Cybernetics & Human Knowing. 8. 3-5.
Peirce and Spencer-Brown on Probability, Chance, and Lawfulness
Author: Martin, J.L.
Source: Cybernetics & Human Knowing, Volume 22, Number 1, 2015, pp. 9-33(25)
Publisher: Imprint Academic
The Mathematics of Charles Sanders Peirce
Louis H. Kauffman1
Cybernetics & Human Knowing, Vol.8, no.1–2, 2001, pp. 79–110
Virtual Logic–The Combinatorial Hierarchy: ‘One, Two, Three, Infinity!’
Author: Kauffman, Louis
Source: Cybernetics & Human Knowing, Volume 19, Number 3, 2012, pp. 83-91(9)
Publisher: Imprint Academic
https://www.ingentaconnect.com/content/imp/chk/2012/00000019/00000003/art00006
A (Cybernetic) Musing: Cybernetics and Circularities
Author: Glanville, Ranulph
Source: Cybernetics & Human Knowing, Volume 19, Number 4, 2012, pp. 105-116(12)
Publisher: Imprint Academic
6.3 One, Two, Three … Eternity
Subchapter in book
Cyber Semiotics: Why Information is not enough
Soren Brier
C. S. Peirce’s Complementary and Transdisciplinary Conception of Science and Religion
Author: Brier, Soeren
Source: Cybernetics & Human Knowing, Volume 19, Numbers 1-2, 2012, pp. 59-94(36)
Publisher: Imprint Academic
Squaring the unknown:
The generalization of logic according to G. Boole, A. De Morgan, and C. S. Peirce
Cassiano Terra Rodrigues
South American Journal of Logic
Vol. 3, n. 2, pp. 415–481, 2017 ISSN: 2446-6719
Mathematical modal logic: A view of its evolution
Centre for Logic, Language and Computation, Victoria University, P.O. Box 600, Wellington, New Zealand
Available online 26 November 2003.
Journal of Applied Logic
Volume 1, Issues 5–6, October 2003, Pages 309-392
https://www.sciencedirect.com/science/article/pii/S1570868303000089
A less simplistic metaphysics: Peirce’s layered theory of meaning as a layered theory of being
Marc Champagne
Department of Philosophy, Trent University 1600 West Bank Drive, Peterborough K9J 7B8, Canada e-mail: marcchampagne@trentu.ca
Peirce’s Existential Graphs — Readings and Links
Dr. Frithjof Dau
http://www.dr-dau.net/eg_readings.shtml
The Graphical Logic of C. S. Peirce
J. J. Zeman:
Existential Graphs
MS 514 by Charles Sanders Peirce
with commentary by John F. Sowa
http://www.jfsowa.com/peirce/ms514.htm
Peirce’s Tutorial on Existential Graphs
John F. Sowa
Semiotica 2011 (186):347-394 (2011)
https://philpapers.org/rec/SOWPTO
Peirce’s Deductive Logic
First published Fri Dec 15, 1995; substantive revision Fri May 20, 2022
SEP Stanford Encyclopedia of Philosophy
https://plato.stanford.edu/entries/peirce-logic/
Diagrams and alien ways of thinking
Marc Champagne
Department of Philosophy, Kwantlen Polytechnic University, 12666, 72 Avenue, Surrey, B.C., V3W 2M8, Canada
Studies in History and Philosophy of Science 75 (2019) 12–22
https://philarchive.org/archive/CHADAA-6
Existential Graphs: What a Diagrammatic Logic of Cognition Might Look Like
Ahti-Veikko Pietarinen
Pages 265-281 | Received 11 Mar 2010, Accepted 06 Jan 2011, Published online: 03 Aug 2011
History and Philosophy of Logic
Volume 32, 2011 – Issue 3
https://doi.org/10.1080/01445340.2011.555506
The Philosophical Context of Peirce’s Existential Graphs
Mary Keeler
University of Washington, Seattle
http://www.welchco.com/02/14/01/60/00/05/1501.HTM
Possibilities in Peirce’s Existential Graphs for Logic Education
Adam Vile and Simon Polovina
GR&ND
South Bank University
Semiotics, Schemata, Diagrams, and Graphs: A New Form of Diagrammatic Kantism by Peirce
Claudio Paolucci
University of Bologna
April 2017
In book: Peirce on Perception and Reasoning. From Icons to Logic.
Hull, K. and Atkins, K. (eds.), Routledge Studies in American Philosophy (pp.74-85)Publisher: Routledge
From Existential Graphs to Conceptual Graphs
John Sowa
VivoMind Resarch, LLC
January 2013
International Journal of Conceptual Structures and Smart Applications 1(1):39-72
DOI:10.4018/ijcssa.2013010103
https://www.researchgate.net/publication/273861229_From_Existential_Graphs_to_Conceptual_Graphs
“75. Visualizing Reason”.
Farias, Priscila L..
Charles Sanders Peirce in His Own Words: 100 Years of Semiotics, Communication and Cognition,
edited by Torkild Thellefsen and Bent Sorensen, Berlin, Boston: De Gruyter Mouton, 2014, pp. 483-486.
https://doi.org/10.1515/9781614516415.483
Existential Graphs and Cognition
Caterina Clivio (Columbia University, USA) and Marcel Danesi (University of Toronto, Canada)
Source Title: Empirical Research on Semiotics and Visual Rhetoric
2018 |Pages: 9
DOI: 10.4018/978-1-5225-5622-0.ch004
https://www.igi-global.com/chapter/existential-graphs-and-cognition/197978
Toward an Integrated History and Philosophy of Diagrammatic Practices
Chiara Ambrosio
Department of Science and Technology Studies UCL
c.ambrosio@ucl.ac.uk
Mathematical Logic with Diagrams Based on the Existential Graphs of Peirce
- F. Dau
- Published 2005
Diagrams as Centerpiece of a Peircean Epistemology
Frederik Stjernfelt
DIAGRAMMATIC THOUGHT: TWO FORMS OF CONSTRUCTIVISM IN C.S. PEIRCE AND GILLES DELEUZE
Kamini Vellodi
PARRHESIA NUMBER 19 • 2014 • 79-95
Charles Sanders Peirce: Logic
IEP
The Semiotics of Spider Diagrams
Jim Burton and John Howse
PEIRCE’S CONTINUUM
A METHODOLOGICAL AND MATHEMATICAL APPROACH
FERNANDO ZALAMEA
Adventures in Diagrammatic Reasoning—A Few Notes
FROM THE SERIES: Graphic Ethnography on the Rise
July 28, 2022
https://culanth.org/fieldsights/adventures-in-diagrammatic-reasoning-a-few-notes
1 Introduction
Andre Freitas
Click to access diagrammatic_quality_semiotica_2019.pdf
Dimensions of Peircean diagrammaticality
Frederik Stjernfelt
Aalborg University
March 2019
Semiotica 2019 (228)
DOI:10.1515/sem-2018-0119
https://www.researchgate.net/publication/331961372_Dimensions_of_Peircean_diagrammaticality
Moving Pictures of Thought
Diagrams as Centerpiece of a Peircean Epistemology
Originally, “Diagrams as Centerpiece in a Peircean Epistemology”, in Transactions of the Charles S. Peirce Society, Summer, 2000, vol. XXXVI, no. 3, 357-92.
In its adapted version, ch. 4 of Diagrammatology. An Investigation in Phenomenology, Ontology, and Semiotics, Dordrecht 2007: Springer Verlag, 89-116.
Click to access Diagrams%20as%20Centerpiece.%202000%3A2007.pdf
Graphs as Images vs. Graphs as Diagrams
A Problem at the Intersection of Semiotics and Didactics
By Michael May
Book
Peirce on Perception and Reasoning
Edition 1st Edition
First Published 2017
Imprint Routledge
Pages 12
eBook ISBN 9781315444642
Diagrams
First published Tue Aug 28, 2001; substantive revision Tue Sep 17, 2013
Stanford Encyclopedia of Philosophy Archive
https://stanford.library.sydney.edu.au/archives/sum2015/entries/diagrams/
Diagrammatic Immanence
Category Theory and Philosophy
Rocco Gangle
2016
Edinburgh University Press Ltd
Existential Graphs as Ontographic Media
Daniela Wentz
2019, Zeitschrift für Medien- und Kulturforschung
https://www.academia.edu/63635014/Existential_Graphs_as_Ontographic_Media
On diagrams for Peirces 10, 28, and 66 classes of signs
Semiotica 2003(147):165-184
DOI:10.1515/semi.2003.089
Priscila Lena Farias
University of São Paulo
Joao Queiroz
Federal University of Juiz de Fora
On the Diversity of Signs in Human Interaction
Jack Sidnell
https://www.academia.edu/36164894/On_the_Diversity_of_Signs_in_Human_Interaction
Semiosis as an Emergent Process
João Queiroz & Charbel Niño El-Hani
Transactions of the Charles S. Peirce Society 42 (1):78-116 (2006)
https://philpapers.org/rec/QUESAA-2
Towards a multi-level approach to the emergence of meaning processes in living systems
João Queiroz & Charbel Niño El-Hani
Acta Biotheoretica 54 (3):179-206 (2006)
https://philpapers.org/rec/QUETAM
Semiotics and Intelligent Systems Development
Ricardo Gudwin
Joao Queiroz
Book 2006
https://www.academia.edu/377806/Semiotics_and_Intelligent_Systems_Development
Images, diagrams, and metaphors: hypoicons in the context of Peirce’s sixty-six-fold classification of signs
Priscila Farias & João Queiroz
Semiotica 2006 (162):287-307 (2006)
https://philpapers.org/rec/FARIDA
10cubes and 3N3: Using interactive diagrams to investigate Charles Peirces classifications of signs
Priscila Farias & João Queiroz
Semiotica 2004 (151):41-63 (2004)
https://philarchive.org/rec/FARCAN?all_versions=1
Notes for a dynamic diagram of Charles Peirce’s classifications of signs
Priscila Farias & João Queiroz
Semiotica 131 (1-2):19-44 (2000)
https://philpapers.org/rec/FARNFA
Bibliography: Advanced Issues on Cognitive Science and Semiotics
Farias, Priscilla & Queiroz, Joao
Year: 2006
Place: Berlin
Publisher: Shaker Verlag
ISBN: 978-3-8322-56
On Peirce’s diagrammatic models for ten classes of signs
Priscila Lena Farias* and João Queiroz
Semiotica 2014; 202: 657 – 671
A String Diagram Calculus for Predicate Logic and C. S. Peirce’s System Beta
G Brady and T H Trimble
1998
http://people.cs.uchicago.edu/~brady/beta98.ps
LOGICAL REASONING WITH DIAGRAMS
edited by GERARD ALLWEIN and JON BARWISE
Oxford University Press
1996
Peirce and Value Theory: On Peircian Ethics and Aesthetics
Herman Parret
John Benjamins Publishing, 1994 – 381 pages
Image Schemas and Conceptual Blending in Diagrammatic Reasoning: The Case of Hasse Diagrams
- September 2021
DOI:10.1007/978-3-030-86062-2_31
- In book: Diagrammatic Representation and Inference, 12th International Conference, Diagrams 2021, Virtual, September 28–30, 2021, Proceedings (pp.297-314)
Euler vs Hasse Diagrams for Reasoning About Sets: A Cognitive Approach
September 2022
DOI:10.1007/978-3-031-15146-0_13
In book: Diagrammatic Representation and Inference (pp.151-167)
Dimitra Bourou
Marco Schorlemmer
Enric Plaza
Spanish National Research Council
https://link.springer.com/chapter/10.1007/978-3-031-15146-0_13
PEIRCE’S THEORY OF ESTHETICS AND NORMATIVE SCIENCE
SEIDENSTICKER, WILLIAM DAVID.
Fordham University ProQuest Dissertations Publishing, 1968. 6902610.
