Indira’s Pearls: Apollonian Gasket, Circle and Sphere Packing
Source: Matrikas

Key Terms
- Circle Packing
- Disk Packing
- Sphere Packing
- Indira’s Net
- Indira’s Pearls
- Apollonian Gasket
- Fractals
- Square and Circle
- Circular Temple
- Earth and Heaven
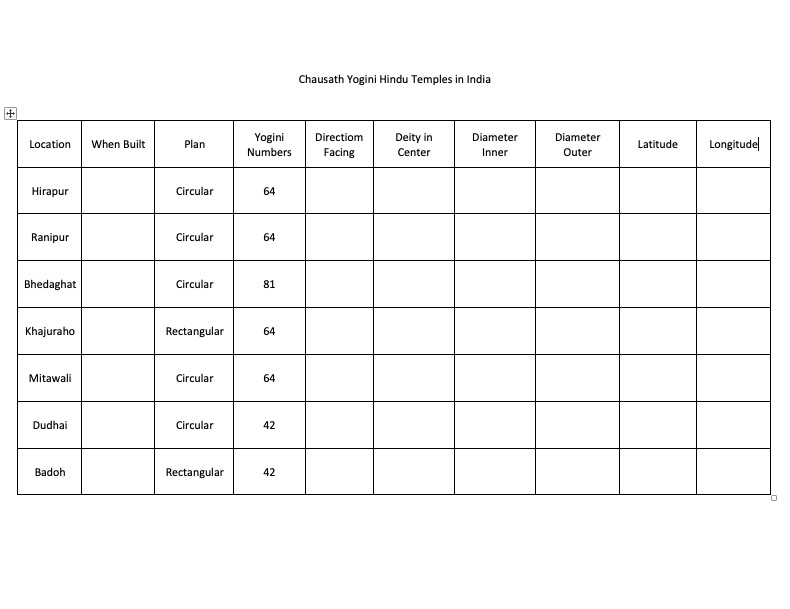
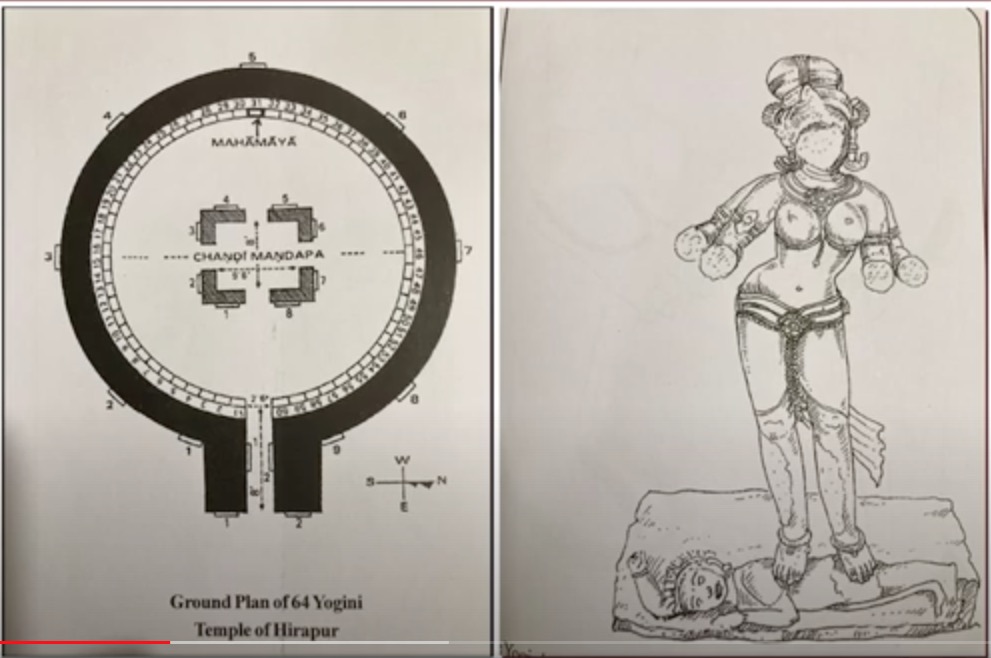
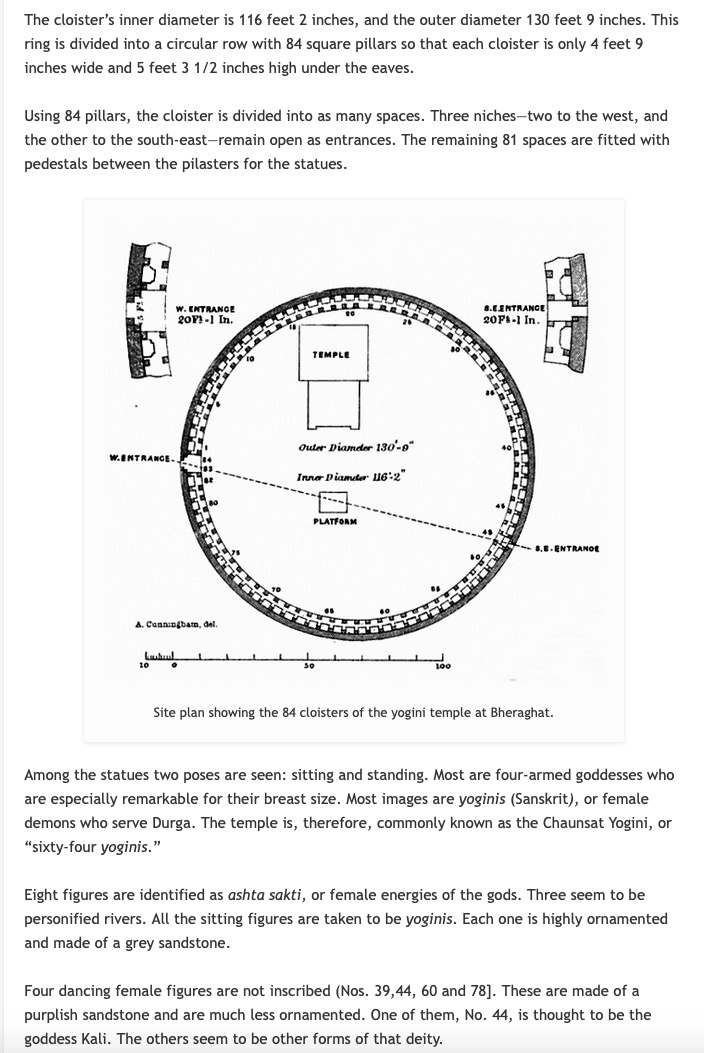
- 64 Yogini Hindu Shakti Temples
- 64 Bhairav
- 64 Yogini
- 7 Matrikas
- Mandala
- Curvilinear Sierpinski Gasket
- Poincare Disc
- Jagannath Puri, Odisha
- Bhuvneswar, Odisha
- Konark, Odisha
- Non Euclidian Geometry
- Euclidian Geometry
- Fractal Geometry
- Sacred Geometry
- Hyperbolic Geometry
- 1, 2, 3 where is the 4th
- 1 2 3 4
- Fifth and Fourth in Music Theory
Fractals, Circle, and Sphere Packing
Source: Circle Packing Explorations

Source: Circle Packing Explorations

Source: On a Diophantine Equation That Generates AllIntegral Apollonian Gaskets
Source:

Source: Recursive Apollonian Gasket

Source: Recursive Apollonian Gasket

Source: Recursive Apollonian Gasket

Source: Recursive Apollonian Gasket

Source: Recursive Apollonian Gasket

Source: On the cover: Apollonian packing
What can you do with this space? So asks Andrew Stacey. ‘Fill it’ is the prompt reply, but fill it with what? Maybe like Andrew you want to use a single curve, but I want to use circles. If you do this in the way shown above in blue, the result is called an Apollonian packing, a variant of which can be seen on the cover of this issue.
Here we shall explore the history of this entrancing object, which spans over 2000 years, and percolates into a surprising variety of mathematical disciplines. Starting in the familiar world of Euclidean geometry, Apollonian packings extend into fractal geometry and measure theory; Möbius transformations and the hyperbolic plane; and then on into the distant reaches of geometric group theory, number theory, orbital mechanics, and even ship navigation.
At times we may wonder off into thickets of more obscure mathematics, so those readers who get lost should feel free to skip ahead to the next section.
Apollonius of Perga
Apollonius (c 230 BC) was a Hellenistic mathematician, considered one of the greatest after Euclid and Archimedes. Perhaps his most important work was his eight book treaties Κωνικα on conic sections—once lost to European civilisation, but fortuitously preserved by the more enlightened Middle Eastern scholars and later reintroduced by Edmund Halley in 1710. The same unfortunately cannot be said of Έπαφαι (De Tractionibus or Tangencies). Although now lost, we have accounts of the work from other ancient authors, particularly in the writings of Pappus of Alexandria. In it, Apollonius posed and solved the following problem.
Problem: Given three geometric objects in the plane (points, lines, and/or circles), find all circles which meet all three simultaneously (ie which pass through any points, and are tangent to any lines or circles).
So for example, given three points which don’t lie on the same line, there is exactly one circle which passes through all three. The case which interests us at present is when we are given three circles, each of which is tangent to the other two. In the very special case that all three are tangent at the same point there are infinitely many circles tangent to all three. Usually, however, the circles will be pairwise tangent at three distinct points, in which case there are exactly two other circles tangent to all three simultaneously.
Given three mutually tangent circles (black) there are usually exactly two others (blue) tangent to all three.
This is as far as Apollonius went; the next step would not be taken until 1643, when René Descartes discovered a formula for the size of the two tangent circles, which he wrote in a letter to Princess Elizabeth of the Palatinate. The same formula was later rediscovered by Frederick Soddy and published as a poem in Nature in 1936.
The size of a circle is determined by its radius rr. If rr is small, the circle will be small, but it will also be very curved. We can define the curvature of the circle to be k=1/rk=1/r. Descartes showed that if three given circles are mutually tangent at three distinct points, and have curvatures k1k1, k2k2, and k3k3, then a fourth circle which is tangent to all three has curvature k4k4 satisfying
(k1+k2+k3+k4)2=2(k21+k22+k23+k24)(1)(1)(k1+k2+k3+k4)2=2(k12+k22+k32+k42)

For technical algebraic reasons, sometimes this equation gives negative values for the curvature k4k4, which we can interpret as corresponding to a circle with curvature |k||k|which contains the other circles in its interior. Notice that this equation is quadratic in the variable k4k4, so there are two solutions; these will correspond to the two possibilities for the fourth circle found by Apollonius.
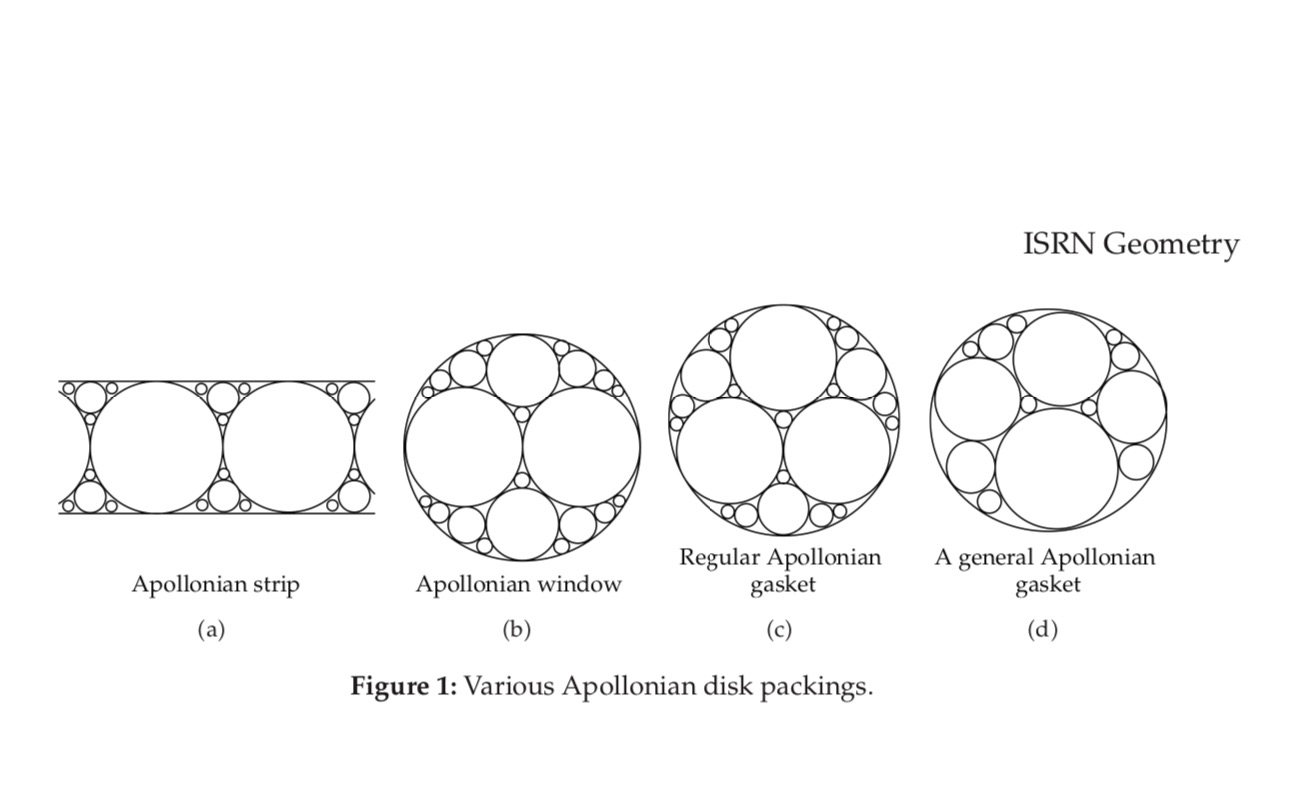
Apollonian packings
So far we have constructed at most 5 mutually tangent circles. The step to infinity may seem obvious, but took another 63 years and some 1900 years after Apollonius. The earliest description seems to appear in a letter from Leibniz to des Bosses (11 March 1706):
Imagine a circle; in it draw three other circles that are the same size and as large as possible, and in any new circle and in the space between circles again draw the three largest circles of the same size that are possible. Imagine proceeding to infinity in this way…
A finite iteration of a nested Apollonian packing similar to the one described by Leibniz. Image: adapted from Todd Stedl, CC BY-SA 4.0
What Leibniz is describing is in fact a nested Apollonian packing, since at each step he fills in every circle as well as the gaps between circles. This early description makes the nested Apollonian packing one of the first fractals, although it wasn’t studied properly until mathematicians like Cantor, Weierstrass, von Koch, and Sierpinski started discovering other fractals in the late nineteenth and early twentieth centuries. This may be because Leibniz was not interested in the mathematical construction, but rather was trying to draw an analogy to argue against the existence in infinitesimals in nature.
Henceforth we shall only consider the un-nested Apollonian packing. As a fractal, it has a number of interesting properties: it is a set of measure 0, which means that if you tried to make it by starting with a disc of metal, and then drilled out infinitely many ever smaller holes (and if you ignore that metal is made out of atoms), then you would finish up with a single piece of metal (you haven’t removed everything), but nevertheless with exactly 0 mass. It has fractal dimension approximately 1.30568, which means that mathematically it lives somewhere between a 1D curve and a 2D area. Finally, if you look at just the portion of an Apollonian packing which lies in the triangular region between three tangent circles, this is homeomorphic to the Sierpinski triangle, which means that one can be bent and stretched to look like the other.
A portion of an Apollonian packing is homeomorphic to the Sierpinski triangle—just squash all of the circles to make them triangular. Images: adapted from Todd Stedl, CC BY-SA 4.0 and Beojan Stanislaus, CC BY-SA 3.0.
There is a curious combinatorial consequence of Descartes’ formula for Apollonian packings. If we start with three mutually tangent circles with curvatures k1k1, k2k2, and k3k3, we can solve (1)(1) to find that the curvatures k+4k4+ and k−4k4− of the other two circles are
k±4=k1+k2+k3±2√k1k2+k2k3+k3k1(2)(2)k4±=k1+k2+k3±2k1k2+k2k3+k3k1
The integral Apollonian packing starting with curvatures -10, 18, 23, and 27. Image: adapted from Todd Stedl, CC BY-SA 4.0.
Now suppose we start constructing an Apollonian packing by drawing four mutually tangent circles whose curvatures k1k1, k2k2, k3k3, and k+4k4+ are all integers. From equation (2)(2) it follows that 2√k1k2+k2k3+k3k12k1k2+k2k3+k3k1 must be an integer since k+4k4+ is an integer, and so k−4k4− is also an integer. Now we can build the packing by filling in a fifth circle wherever we see four mutually tangent circles. By the observation above, if the four circles have integer curvatures, the fifth circle will also have integer curvature. Inductively therefore we will end up with an Apollonian packing consisting of infinitely many tangent circles, all of which have integer curvatures.
Hyperbolic geometry
All these scorpions have the same hyperbolic size.
If you have some familiarity with non-Euclidean geometry, Apollonian packings may remind you of the Poincaré model of the hyperbolic plane. The hyperbolic plane H2H2 is a 2D surface on which we can do geometry just like we can on the flat Euclidean plane. Whereas a sphere has constant positive curvature (it curves the same way in all directions), and the Euclidean plane has constant zero curvature (it’s flat), H2H2 is an infinite surface which has constant negative curvature, which means that at every point it curves in the same way as a Pringle. This negative curvature makes the surface crinkle up on itself more and more as you move out towards infinity, which is inconvenient when we try to work with it. Usually then we represent it on a flat surface so we can draw pictures of it in magazines and the like. One way to do this is with the Poincaré model. This views the hyperbolic plane as a disc. In order to fit the whole infinity of H2H2 into a finite disc, we have to shrink distances as we move out towards the edge of the disc. Using this skewed way of measuring distances, the circular edge of the disc is infinitely far away from its centre.
We can think of an Apollonian packing as living in the Poincaré disc, with the outermost circle of the packing as the boundary circle of H2H2. Then the circles in the packing which are not tangent to this boundary are also circles in the strange hyperbolic way of measuring distance, that is, all points are equidistant from some other point in the plane—the circle’s hyperbolic centre. Circles in the packing which are tangent to the boundary are called horocycles (in Greek this literally means border circle), which are circles with infinite radius in the hyperbolic metric. Horocycles have no analogue in the Euclidean plane.
Something interesting happens when we see what an Apollonian packing looks like in the upper half-plane (UHP) model for H2H2. This model is similar to the Poincaré model, but instead of using a disc, we use the half-plane above the xx-axis {(x,y)∈R2:y>0}{(x,y)∈R2:y>0}, where the xx-axis behaves like the boundary circle and should be thought of as at infinity. There is a problem, in that in the Poincaré disc, the boundary of H2H2 was a circle, and so it closed up on itself. In the UHP, the boundary is a line which doesn’t close up on itself, but these are supposed to be models for the same thing. To fix this, we imagine there is a point at infinity ∞∞ which joins up the two ends of the boundary to form an infinite diameter circle.
If we start with any Apollonian packing living in the Poincaré disc, there is a map from the disc to the UHP preserving hyperbolic distances, under which the outer circle of the packing becomes the xx-axis (together with the point at infinity), and exactly one of the horocycles (one of the circles tangent to the outer circle in the packing) becomes the horizontal line y=1y=1. All other circles and horocycles in the packing are sent to circles which are tangent to each other as before, but are now sandwiched between the lines y=0y=0 and y=1y=1.

If we focus on just those circles which meet the xx-axis we get what are called Ford circles. Remarkably each of these circles is tangent to the xx-axis at a rational number p/qp/q, and has radius 1/2q21/2q2. Moreover every rational number is the point of tangency of one of the circles (see below). Now some magic happens: suppose the Ford circles at a/ba/b and c/dc/d are tangent to each other, then there is a unique circle sandwiched between these two circles and the xx-axis. The rational point at which this circle meets the xx-axis is given by the Farey sum of a/ba/b and c/dc/d
ab⊕cd=a+bc+dab⊕cd=a+bc+d

Note that for this to be well-defined, a/ba/b and c/dc/d must be written in their simplest form. This Farey sum, and the associated Farey sequences FnFn you get by looking at all rational numbers between 0 and 1 which can be written as a fraction with denominator at most nn, turn up in several places across number theory. These include rational approximation of irrational numbers and the Riemann Hypothesis.
Möbius transformations
If you haven’t seen hyperbolic geometry before, you may wonder how we can map the Poincaré disc model to the UHP model, and in such a way that the strange distance measure in the two models is preserved—for a start one is a finite region while the other is an infinite half-plane. The answer is to view both models as living inside the complex plane CC (or more accurately the extended complex plane ˆC=C∪{∞}C^=C∪{∞}): the Poincaré disc is the unit disc {z∈C:|z|<1}{z∈C:|z|<1}, and the UHP is the region above the real axis {z∈C:{z∈C: Im(z)>0}(z)>0}. Then a function like
z↦−iz+1z−1=−iz−iz−1(3)(3)z↦−iz+1z−1=−iz−iz−1
will do the trick. This function is an example of a Möbius transformation, which in general is a complex function of the form
z↦az+bbz+dz↦az+bbz+d
were we require ad−bc≠0ad−bc≠0 so that this function is invertible. The function (3)(3) sends the unit disc to the UHP, but it is not the only Möbius transformation which does this. In fact there are infinitely many such functions, all of which preserve the hyperbolic metric. In the previous section I claimed that starting with any Apollonian packing, we could choose one of these Möbius transformations such that the image had a very specific form, sandwiched between the lines Im(z)=0(z)=0 and Im(z)=1(z)=1.
An exercise: If you have seen Möbius transformations before, you may wish to try and prove that the purported mapping exists yourself. (Hint: remember that Möbius transformations send circles and lines to circles and lines, and are completely determined by their image on 3 distinct points.)
The upshot of this is that all Apollonian packings are the same in the hyperbolic plane, because they can all be mapped to the same packing by (invertible) functions which preserve hyperbolic distance. Once we have started thinking about the Apollonian packing living in the complex plane, the whole world of complex functions is open to us, and we can start to do crazy things. If we don’t restrict ourselves to just Möbius transformations, but see what happens when we apply holomorphic or anti-holomorphic functions to the packing (these are complex functions with a good notion of derivative in the sense of calculus, which in particular have the property that they preserve angles between intersecting curves), we can get some very pretty designs. We need not even require (anti-)holomorphicity. The patterns featured on the front and back covers were drawn in this way.
Beyond the packing
Let us return to Apollonius of Perga. Remember that his treaties Έπαφαι, where he stated and solved the problem of finding tangent circles, is lost to history—how then do we know what he proved and how? The answer is that we don’t. The only record we have appears in the writings of Pappus of Alexandria, who lived some 400 years after Apollonius, but who references many of Apollonius’ works, including six which are no longer extant. All he says of Tangencies is the general problem which Apollonius was interested in, and that he solved it by solving many simple special cases and working up from there.
The first person to reprove Apollonius’ results in ‘modern’ times was Adriaan van Roomen in 1596. His solution, however, does not use ruler and compass constructions, so cannot have been the one Apollonius used. The result was later proved using methods available to Apollonius, and in the way described by Pappus, by van Roomen’s friend François Viéte.
A ship’s location determined by its distance from three points.
The method of Viéte was later reworked and simplified by several mathematicians, including Isaac Newton in his Principia. Newton related the position of the centre of the fourth circle to its distance from the centres of the three circles to which it is supposed to be tangent. This is called hyperbolic positioning or trilateration. Newton used this viewpoint to describe the orbits of planets in the solar system, but it can also be used to help navigate ships, and to locate the source of a signal based on the different times the signal is received at three different locations. In the first world war this was used to locate artillery based on when shots were heard. This is also how modern GPS works (not by triangulation as is commonly believed).
So this 2000-year-old problem in abstract geometry turned out to have extremely useful applications in the real world. The Apollonian packing also shows up in lots of different areas of mathematics. For example, Ford circles inspired the Hardy–Littlewood circle method, an important tool in analytic number theory which was used to solve Waring’s Problem: for an integer kk, can every integer be written as a sum of at most nn kkth powers for some value of nn? This is true: for example, every integer is the sum of 4 squares, 9 cubes, 19 fourth powers, and so on. In 2013, Harald Helfgott used the circle method to prove the weak Goldbach conjecture: every odd number greater than 5 is the sum of 3 primes.
To infinity
As a final application, I am a geometric group theorist, and I cannot help but talk about one place the Apollonian packing shows up in my field. Be warned: there is definitely some advanced maths coming up, but if you don’t mind skipping over some of the details, there are some very pretty pictures to make it worthwhile.
It turns out that the extended complex plane ˆCC^ can be thought of as the boundary of 3 dimensional hyperbolic space H3H3. If we model H3H3 as the upper half-space {(x,y,z)∈R3∣z≥0}∪{∞}{(x,y,z)∈R3∣z≥0}∪{∞} then ˆCC^ is identified with the plane {(x,y,z)∈R3∣z=0}∪{∞}{(x,y,z)∈R3∣z=0}∪{∞}. When Möbius transformations act on ˆCC^, they also act on the whole of H3H3, and preserve hyperbolic distance. If we start by choosing just a few Möbius transformations, these generate a group which acts on H3H3. In doing so, the group creates a pattern on the complex plane called its limit set. This is a picture of how the group acts ‘at infinity’. Choosing the Möbius transformations carefully gives a group whose limit set is precisely the Apollonian packing.
A valid arrangement of circles, with their interiors shaded. Note that the straight line is an infinite radius circle through ∞∞, so it still counts.
Let’s be a bit more precise; pick a point p∈ˆCp∈C^ and choose gg pairs of circles (C+i,C−i)gi=1(Ci+,Ci−)i=1g, each of which doesn’t intersect pp. Each circle cuts ˆCC^ into two regions, call the region containing pp the exterior of that circle, and the complementary region the circle’s interior. We also want to arrange things so that no two circles have overlapping interiors (although two circles are allowed to be tangent). Next, for each pair of circles (C+i,C−i)(Ci+,Ci−) choose a Möbius transformation mimiwhich maps C+iCi+ to C−iCi− and which sends the interior of C+iCi+ to the exterior of C−iCi−. The group G=⟨m1,…,mg⟩G=⟨m1,…,mg⟩ generated by these transformations is called a (classical) Schottky group and it acts as a subgroup of the group of isometries of H3H3. Since we chose the circles to have non-overlapping interiors, we can use the delightfully named ‘Ping-Pong Lemma’ to prove that GG is abstractly isomorphic to the free group on gggenerators.
A packing with the four starting circles emphasised in black, and the Schottky group generators shown in pink and blue.
So how do we get a Schottky group whose limit set is the Apollonian packing? We can cheat slightly by working backwards; starting off with the picture we want to create, then we will choose the pairs of circles in the right way. Remember that one way we thought about constructing the Apollonian packing was to start off with four mutually tangent circles and then inductively draw the fifth circle wherever we can. Our strategy will be to choose Möbius transformations which do the same thing. We are helped by the following curious fact which you may want to try and prove yourself (again using Möbius transformations): given any three mutually tangent circles, there is a unique circle (possibly through ∞∞) which passes through all three circles at right angles. Given the four initial circles, there are (43)=4(43)=4 triples of mutually tangent circles, so we let C±1C1± and C±2C2± be the four circles orthogonal to each of these triples, as shown on the left. The corresponding Möbius transformations are :
m1:z↦z−2iz+1m2:z↦(1−i)z+1z+(1+i)m1:z↦z−2iz+1m2:z↦(1−i)z+1z+(1+i)
The limit set of G=⟨m1,m2⟩G=⟨m1,m2⟩ is indeed the Apollonian packing we started with. If we perturb the starting Möbius transformations just slightly by varying the matrix entries (while being careful to ensure that the resulting group acts nicely on H3H3), we get a group whose limit set is a twisted Apollonian packing.
The limit sets of a one parameter family of groups which contains the Schottky group GG. Click the image to view a higher quality version.
Even though some of these perturbed limit sets look like they are still made up more or less of circles, they are in fact made up of a single continuous closed curve which is fractal, and does not intersect itself anywhere. They are examples of Jordan curves and illustrate why the Jordan Curve Theorem is so difficult to prove despite being ‘obvious’. Playing around more with different choices of Möbius generators we can produce even more beautiful examples of fractal limit sets; below are just a few to finish off. If you want to learn more about Schottky groups, their limit sets, and how to draw these pictures, I highly recommend the book Indra’s pearls: the vision of Felix Klein. It is the basis of this final section of this article, and gives details on exactly how you can draw these and many other pictures yourself.

David Sheard
Source: The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry

Source: The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry

Source: The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry

Source: The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry

Source: Circle patterns in Gothic Architecture

My Related Posts
Indra’s Net: On Interconnectedness
Charles Sanders Peirce’s Visual Logic: Diagrams and Existential Graphs
A Calculus for Self Reference, Autopoiesis, and Indications
64 Yogini Hindu Temples Architecture
Fractal Geometry and Hindu Temple Architecture
Consciousness of Cosmos: A Fractal, Recursive, Holographic Universe
Mind, Consciousness and Quantum Entanglement
Cantor Sets, Sierpinski Carpets, Menger Sponges
Interconnected Pythagorean Triples using Central Squares Theory
Key Sources of Research
ON A DIOPHANTINE EQUATION THAT GENERATES ALL APOLLONIAN GASKETS
JERZY KOCIK
Volume 2012 | Article ID 348618 | https://doi.org/10.5402/2012/348618
Click to access Diophantine.pdf
Circle Packing Explorations.
Francesco De Comite ́
Laboratoire d’Informatique Fondamentale de Lille
University of Sciences and Technology of Lille , France
Francesco.De-Comite@univ-lille1.fr
Bridges 2013: Mathematics, Music, Art, Architecture, Culture, 2013,
Enschede, Netherlands. pp.399–402. hal-00861402
https://www.researchgate.net/publication/278769035_Circle_Packing_Explorations
Circle patterns in Gothic Architecture
Tiffany C. Inglis and Craig S. Kaplan
Published 2012
David R. Cheriton School of Computer Science
University of Waterloo
piffany@gmail.com
Bridges 2012: Mathematics, Music, Art, Architecture, Culture
https://www.semanticscholar.org/paper/Circle-patterns-in-Gothic-Architecture-Kaplan/da91338728b153b9785913d43199a4227853365a
Concept cathedral and “squaring the circle”: Interpreting the Gothic cathedral of Notre Dame de Paris as a standing hymn
Nelly Shafik Ramzy
Department of Architectural Engineering, Faculty of Engineering, Benha University, El Kalyobia, Egypt
Frontiers of Architectural Research
Volume 10, Issue 2, June 2021, Pages 369-393
https://doi.org/10.1016/j.foar.2021.02.001
https://www.sciencedirect.com/science/article/pii/S209526352100008X
The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry
Nelly Shafik Ramzy
Sinai University
Peregrinations: Journal of Medieval Art and Architecture
Volume 5 Issue 2 135-172
2015
QUADRALECTIC ARCHITECTURE – A Panoramic Review
by Marten Kuilman
Posted on 26 Aug 2013 by quadralectics
Falcon Press (2011) – ISBN 978-90-814420-0-8
https://quadralectics.wordpress.com
An Introduction to the Apollonian Fractal
Paul Bourke
Email: pdb@swin.edu.au
Swinburne University of Technology P. O. Box 218, Hawthorn Melbourne, Vic 3122, Australia.
http://paulbourke.net/papers/apollony/
http://paulbourke.net/fractals/apollony/
Apollonian gaskets and circle inversion fractals
Estimate for the fractal dimension of the Apollonian gasket in d dimensions.
Farr RS, Griffiths E.
Phys Rev E Stat Nonlin Soft Matter Phys. 2010 Jun;81(6 Pt 1):061403. doi: 10.1103/PhysRevE.81.061403. Epub 2010 Jun 24. PMID: 20866417.
https://pubmed.ncbi.nlm.nih.gov/20866417/
On the cover: Apollonian packing
David Sheard explores the rich mathematics and history behind the Apollonian packing, and the cover of issue 11
David Sheard
17 April 2020
On the cover: Apollonian packing
Recursive Apollonian Gasket
Photostream on Flickr
by FDeComite
2011
Quadrilaterals & Triangles
Malin Christersson
2019
http://www.malinc.se/math/geometry/pythagorasen.php
Apollonian circle packings: Dynamics and Number theory
Hee Oh
Yale University
ICWM, 2014
SINGLE LINE APOLLONIAN GASKETS:
IS THE LIMIT A SPACE FILLING FRACTAL CURVE?
L.M.G. FEIJS
University of Technology Eindhoven and LAURENTIUS LAB. Sittard (The Netherlands) l.m.g.feijs@tue.nl
Spatial Statistics of Apollonian Gaskets,
Weiru Chen, Mo Jiao, Calvin Kessler, Amita Malik & Xin Zhang (2019)
Experimental Mathematics, 28:3, 263-270,
DOI: 10.1080/10586458.2017.1385037
Revisiting Apollonian gaskets
Published: Sat 06 August 2022
By Alden Bradford
In Blog.
https://aldenbradford.com/revisiting-apollonian-gaskets.html
Matrikas
Wikipedia
https://en.wikipedia.org/wiki/Matrikas
Indra’s Pearls: The Vision of Felix Klein.
David Mumford, Caroline Series, and David Wright.
Cambridge University Press,Cambridge, 2002.
Geometry in Art and Architecture
Paul Calter
https://math.dartmouth.edu/~matc/math5.geometry/syllabus.html
The Circular Church Plan
Quadralectic Architecture