Tag: Cellular Automata

Fractal Geometry and Hindu Temple Architecture

Fractal Geometry and Hindu Temple Architecture

Source: Mandapa: Its Proportion as a tool in Understanding Indian Temple Architecture

Proportion and measurements were the guiding tools for Indian temple construction starting from the 5th century onwards and it continuous even now. Through out the history proportion dominated as a tool, which determined the monuments both spatial arrangements as well as form. The ancient texts, therefore, insist on a high degree of precision in their measurements.

The standard text Mayamata mentions- ”Only if the temple is constructed correctly according to a mathematical system can it be expected to function in harmony with the universe. Only if the measurement of the temple is in every way perfect, there will be perfection in the universe as well.”

Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

Source: TEMPLE ARCHITECTURE AND SCULPTURE

Source: Symbolism in Hindu Temple Architecture and Fractal Geometry – ‘Thought Behind Form’

Source: TEMPLE ARCHITECTURE AND SCULPTURE

Source: TEMPLE ARCHITECTURE AND SCULPTURE

Key Terms

  • Fractals
  • Cosmology
  • Temple Architecture
  • Fractal Dimension
  • Recursive
  • Algorithmically
  • Hindu Temples
  • Vastu Purush Mandala
  • Vastu Shastra
  • Shilpa Shastra
  • Nagara Style
  • Dravidian Style
  • Vesara Style
  • Kalinga Style
  • 64 Yogini Temple Style
  • Jain Temple Architecture
  • Buddhist Stupa Architecture
  • Cellular Automata
  • 3D Fractals
  • 2D Cellular Automata
  • Nine Cell Square
  • Nav Grah Yantra
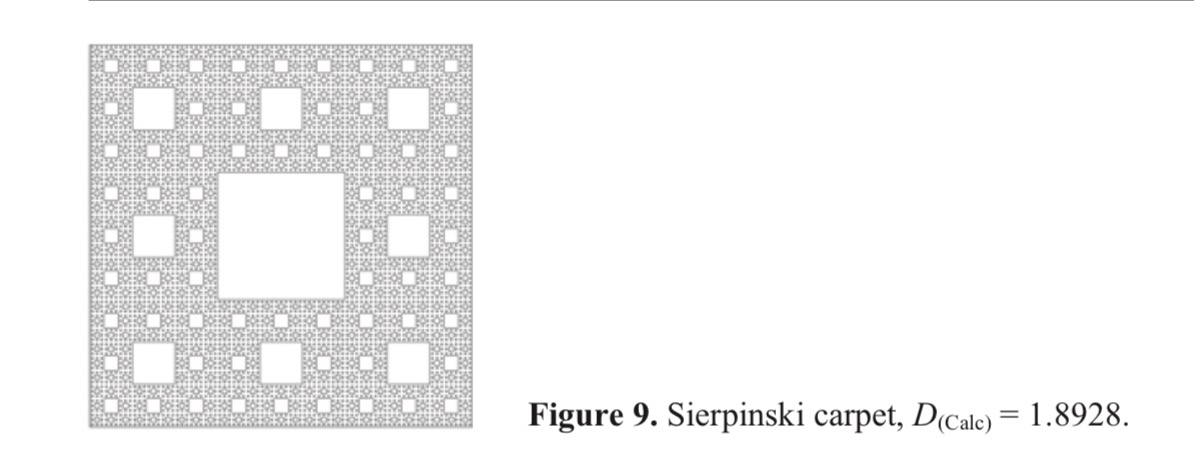
  • Sierpinski Carpet
  • Box Counting Method
  • Biophilic Architecture
  • Symbolism
  • Square and Circle
  • Earth and Heaven
  • Squaring the Circle
  • Correspondence
  • Equivalence
  • Symmetry
  • As Above, So below
  • Cosmic Mirrors

Hindu Temples: Models of a Fractal Universe

Source: Hindu temples: Models of a fractal universe

Hindu philosophy views the cosmos to be holonomic and self-similar in nature. According to ancient architectural tradition, Hindu temples are symbols of models of the cosmos and their form represents the cosmos symbolically.

The procedures and methods used in the construction of Hindu temples bear a striking resemblance to the procedures of computer graphics, including discretization, fractalization and extensive use of recursive procedures, including self-similar iteration. The instructions given in ancient Vastu shastras (texts on architecture) work like general programmes to generate various types of temples.

The paper is an attempt to draw attention to the similarities between the procedures and resulting forms in computer graphics and Hindu temple architecture and to explain the relationship that exists between the form of the temple and the concepts of Hindu philosophy. It is proposed that Hindu temples may be viewed as three dimensional fractal models and that the use of fractal geometry procedures has a special symbolic meaning in the generation of the forms of Hindu temples.

Introduction to the Temple Architecture in the Indian Context

Source: Temples of Odisha- the Geometry of Plan Form

The evolution of temple architecture is marked by a strict adherence to the original ancient models, that were derived from sacred thought which persisted over many centuries. The commencement of the main style of Hindu temple architecture in India dates back to the Mauryan period i.e 3rd century BC, as evident from the archaeological excavation at Sanchi (Madhya Pradesh, temple no.40 and18) and Bairat (Rajastan), (DB Garnayak , 2007) . The Indian Silpasastras recognize three main types of temples known as the Nagara, Dravida and Vesara. Nagara temple belongs to the country from the Himalaya to the Vindhya, Vesara from the Vindhya to the Krishna and the Dravida from the Krishna to the Cape Comorin (DB Garnayak , 2007). An inscription in 1235 A.D in the mukhamandapa of the Amritesvara temple at Holal in Bellary district of Karnataka speaks of the fourth style i.e. Kalinga, in addition to the above three. The Kalinga style of Architecture is explained exclusively in the texts like Bhubana Pradip, Silpa Prakasa, Silpa Ratnakosha etc.

Source: Investigating Architectural Patterns of Indian Traditional Hindu Temples through Visual Analysis Framework

Source: Fractal Geometry as a source of innovative formations in interior design

Source: The fractal analysis of architecture: calibrating the box-counting method using scaling coefficient and grid disposition variables

Source: PARAMETRIZING INDIAN KARNATA-DRAVIDA TEMPLE USING GEOMETRY

Vastu purusha mandala

Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

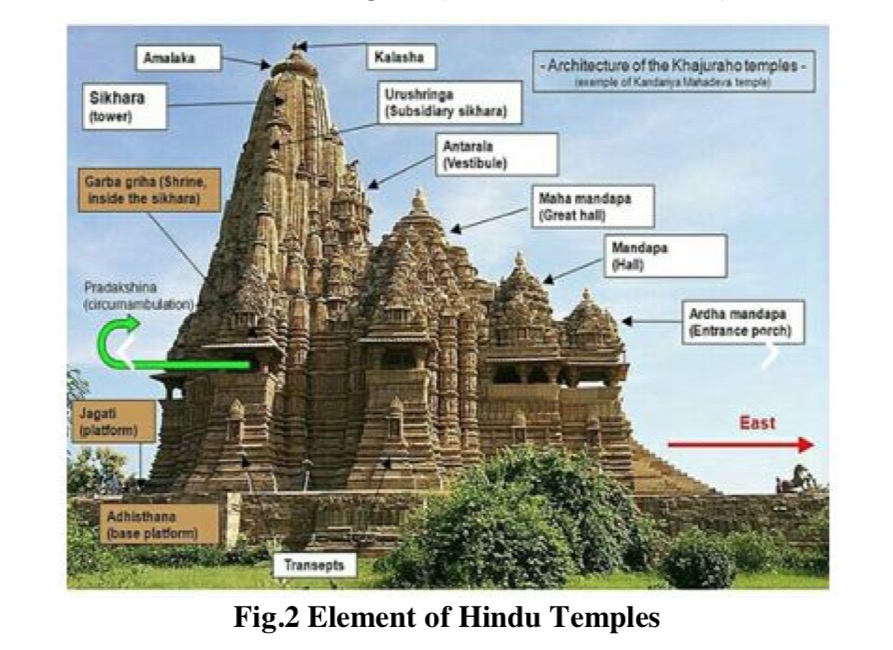
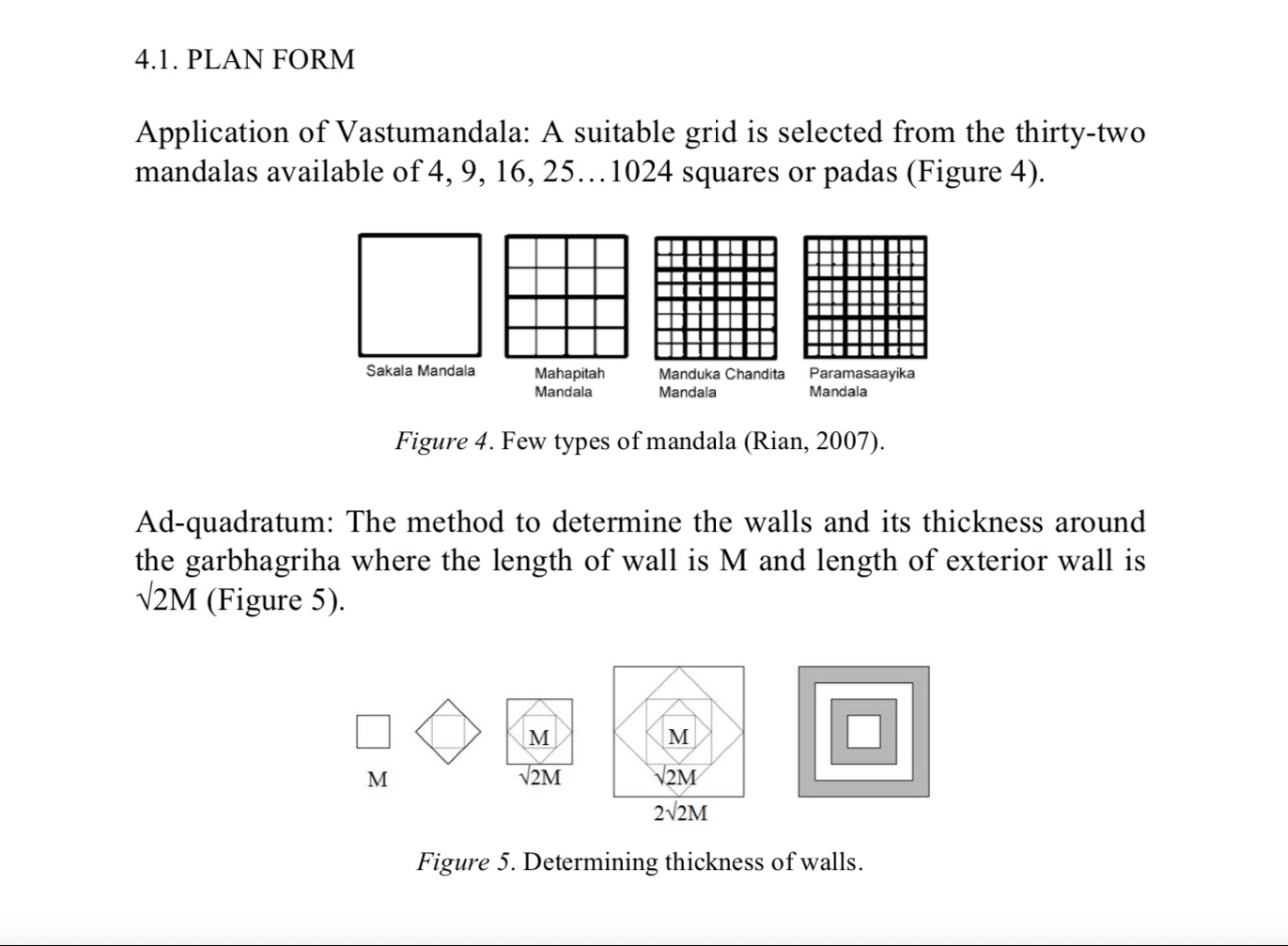
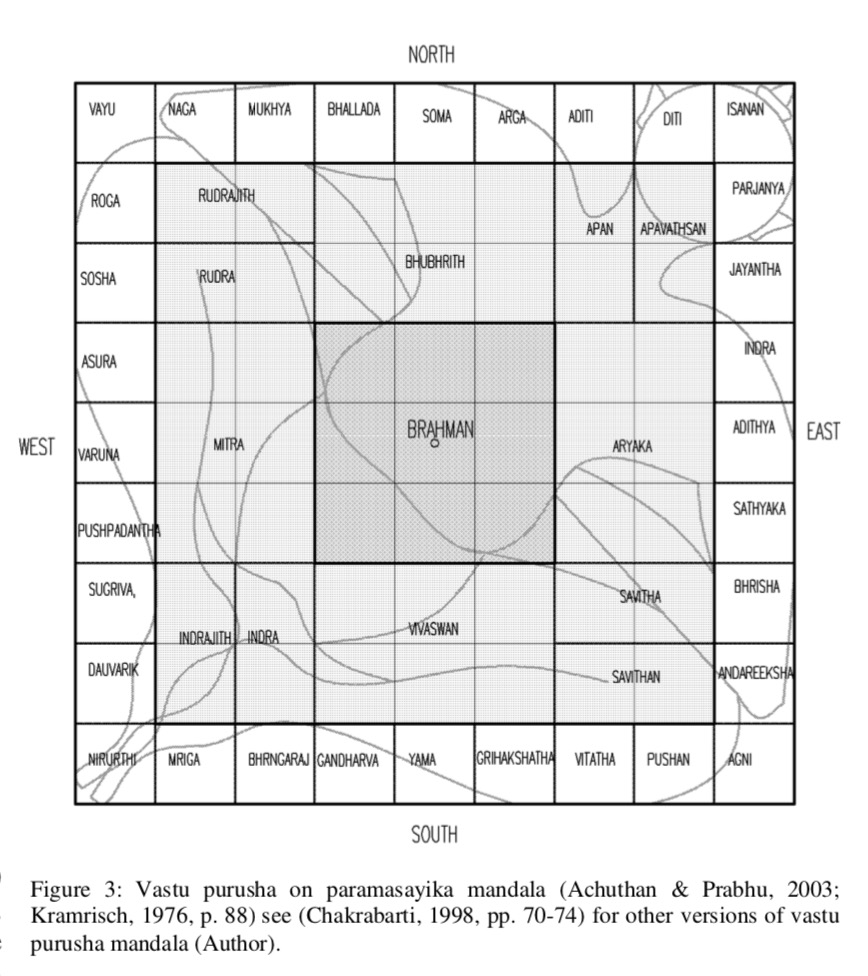
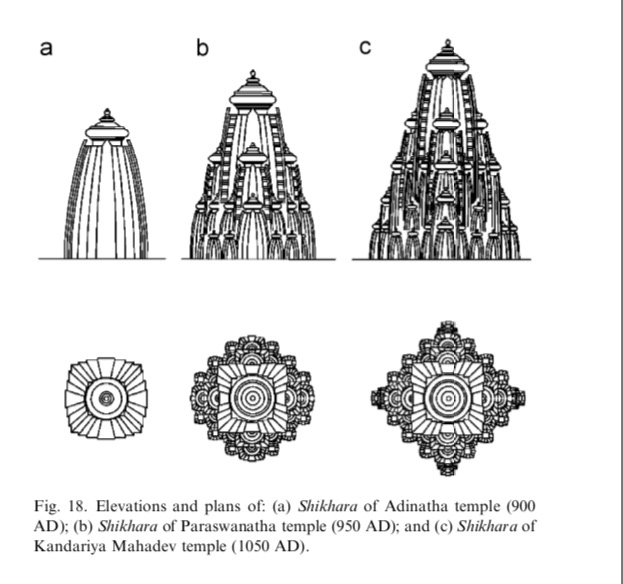
Layout of a Hindu temple pursues a geometrical design known as vastu-purusha-mandala, the name of which is derived from the three vital components of the design namely Vastu meaning Vaas or a place of dwelling; Purusha, meaning the Universal principle; and Mandala meaning circle. Vastupurushamandala is a mystical diagram referred in Sanskrit as a Yantra. The symmetrical and self-repeating model of a Hindu temple demonstrated in the design is derived from the primary convictions, traditions, myths, fundamentality and mathematical standards. According to Vastupurushamandala, the most sacred and typical template for a Hindu temple is the 8×8 (64) grid Manduka Hindu Temple Floor Plan also referred as Bhekapada and Ajira. The layout displays a vivid saffron centre with intersecting diagonals which according to Hindu philosophy symbolises the Purusha. The axis of the Mandir is created with the aid of the four fundamentally significant directions and thus, a perfect square is created around the axis within the available space. This square which is circumscribed by the Mandala circle and divided into perfect square grids is held sacred. On the other hand, the circle is regarded as human and worldly that can be perceived or noticed in daily life such as the Sun, Moon, rainbow, horizon or water drops. Both the square and the circle support each other. The model is usually seen in large temples while an 81 sub-square grid is observed in ceremonial temple superstructures. Each square within the main square referred as „Pada‟ symbolise a specific element that can be in the form of a deity, an apsara or a spirit. The primary or the innermost square/s of the 64 grid model called Brahma Padas is dedicated to Brahman. The Garbhagruha or centre of the house situated in the Brahma Padas houses the main deity. The outer concentric layer to Brahma Padas is the Devika Padas signifying facets of Devas or Gods which is again surrounded by the next layer, the Manusha Padas, with the ambulatory. The devotees circumambulate clockwise to perform Parikrama in the Manusha Padas with Devika Padas in the inner side and the Paishachika Padas, symbolising facets of Asuras and evils, on the outer side forming the last concentric square. The three outer Padas in larger temples generally adorn inspirational paintings, carvings and images with the wall reliefs and images of different temples depicting legends from different Hindu Epics and Vedic stories. Illustrations of artha, kama, dharma and moksha can be found in the embellished carvings and images adorning the walls, ceiling and pillars of the temples.

Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

Source: VASTU PURUSHA MANDALA- A HUMAN ECOLOGICAL FRAMEWORK FOR DESIGNING LIVING ENVIRONMENTS

Source: Space and Cosmology in the Hindu Temple

Source: Exploring Ancient Architectural Designs with Cellular Automata

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

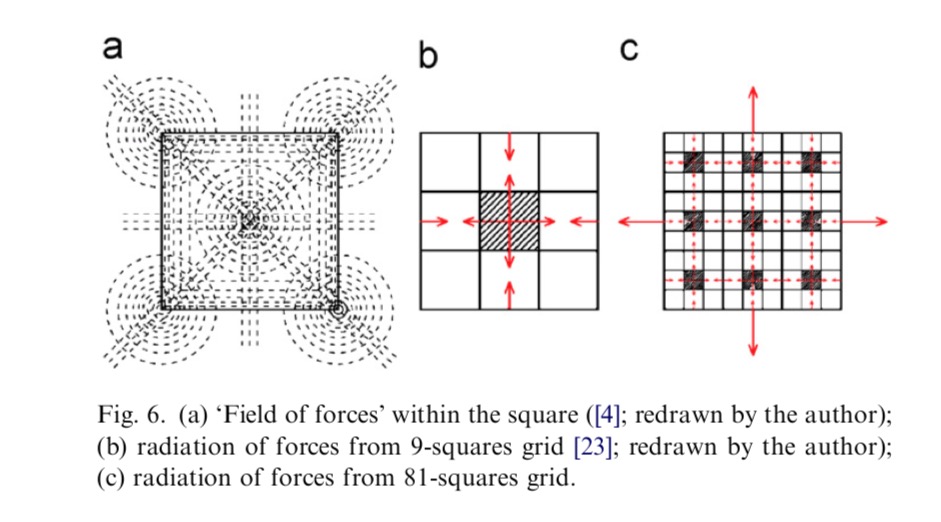
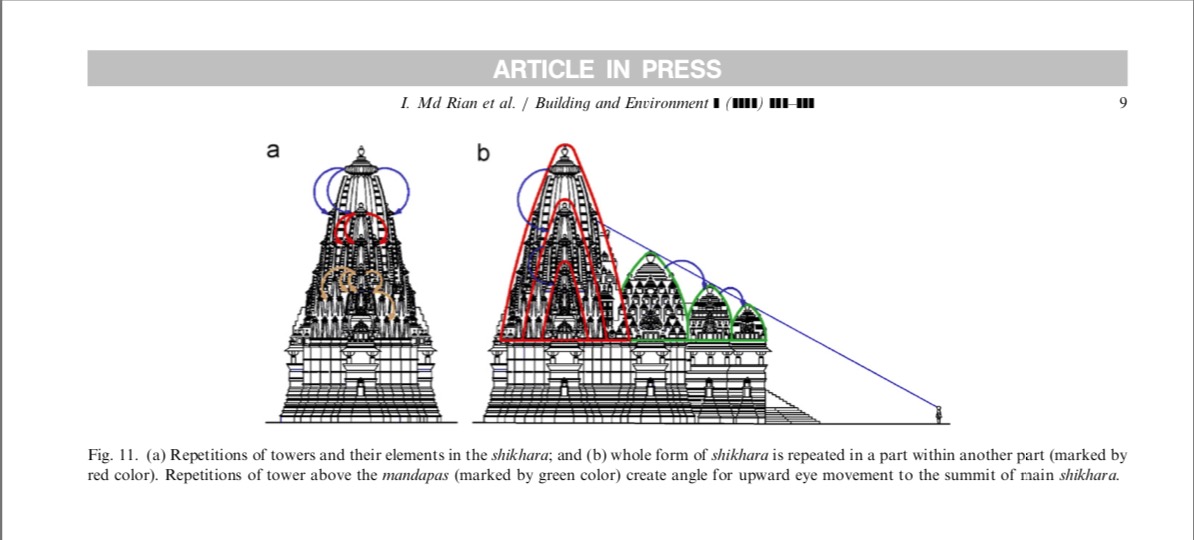
According to Hindu philosophy, the main goal of man’s life is to achieve the ultimate liberation from the illusionary world where he suffers from his endless rebirth. Krishna says in Bhagavad Gita,9 if man worships, devotes and meditates to the manifested form of the wholeness of infinity, and sees the truth of its manifestation; he will surpass the confusion of the never-ending cycles of rebirth in this physical world, and finally will assimilate with the God. 10 Hindu calls it moksha.11 It brings the ultimate peace and harmony in man’s life. But how one, from the physical world, can practice to realize this ultimate truth of the creation? Brihatsamhita12 and Sthapatyaveda13 give the solution as the temple which should act as the microcosm of the cosmos [9]. It should be the bridge for the man of physical world to the God of divine world [10].

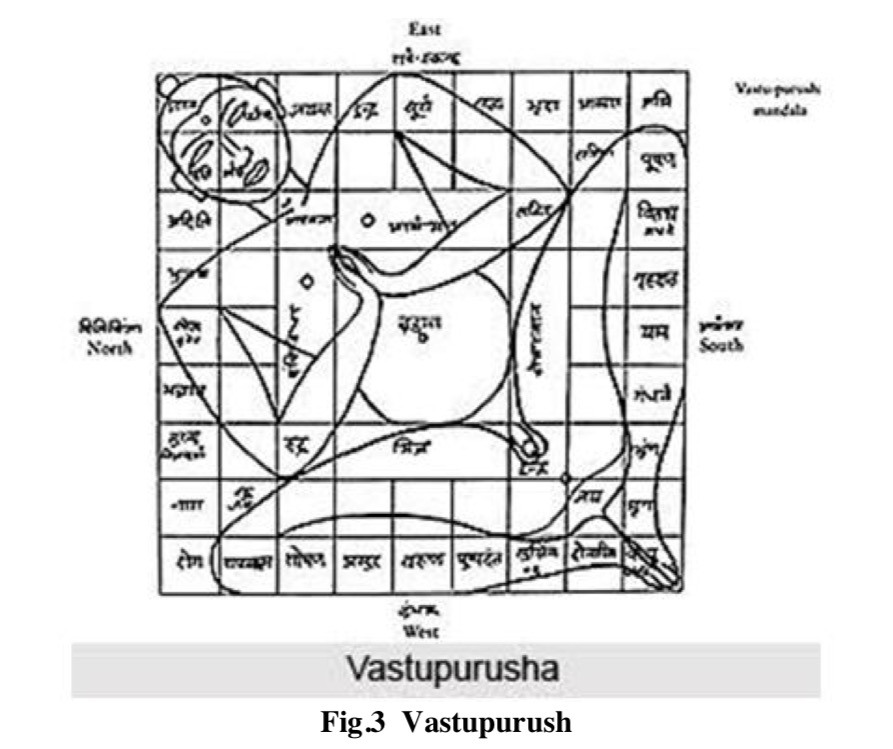
To connect the physical world with the divine world and to reflect the truth of creation, the layout of cosmos was copied graphically in the foundation of temple. Here, a mythical incident was interwoven where a formless being covered the sky and was, immediately, arrested down to the earth by the creator Brahma and other gods. This supernatural fact was depicted graphically by vastu purusha mandala, where vastu refers to physical environment, purusha refers to energy, power or cosmic being, and mandala is the diagram or chart. Central portion of the mandala represents the place of Brahma and other portions symbolize the other gods according to their capability. By laying down this metaphysical diagram in the foundation, various supernatural forces are captured beneath the temple whereas its centre is the source of cosmic energies. The basic shape of the vastu purusha mandala is a square which represents the earth [11]. Its four sides depict the four cardinal directions. It also symbolizes the order, the completeness of endless life and the perfectness of life and death [10]. According to Hindu philosophy, our mundane life is controlled by the number four—four castes, four stages of life, four great epochs or mahayugas, four heads of Brahma, the four Vedas etc. [12].

There are various types of vastu purusha mandala, which are nothing but the squares grids, produced from the basic shape; namely, a square which is known as sakala mandala. Each smaller square within the grid is called one pada. The number of pada may vary from 1, 4, 9, 16, 25 and so on 1024, where it follows the geometric progression of 1, 2, 3, 4, 5,…..,32 of common ratio 2. The mandala having even numbers of pada in its grid known as yugma squares mandala whereas the mandala, having odd numbers of pada known as ayugma squares mandala. Vastu purusha mandala is also known as different distinctive names according to the numbers of pada within the grid. The mandala having 1,4,9,16,25 and 36 numbers of pada within the grid are known as sakala mandala, pechaka mandala, pitah mandala, mahapitah mandala, manduka chandita mandala and para- masayika mandala, respectively14.

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

FRACTAL DESIGN, ARCHITECTURE AND ART IN HUMAN HISTORY

Source: Working with Fractals

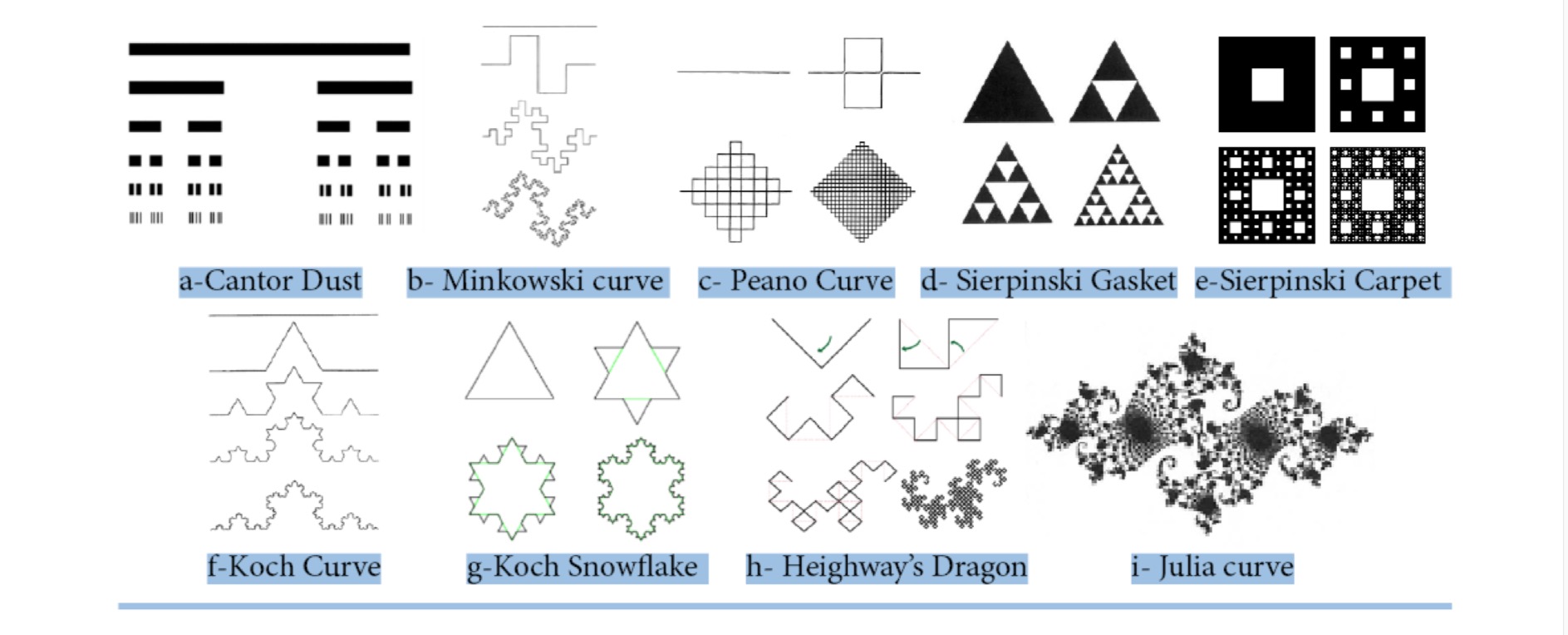
Fractals have permeated cultures spanning across many centuries and continents, classical art and vernacular architecture from the column capitals of ancient Greece, Egyptian, Aztec, Incan civilisations, the art of Ancient Mayans, Islamic and Hindu temples, Angkor Wat in Cambodia, the Eifel Tower in Paris, and the structures of Santiago Calatrava. Fractals are also evident in such well known works as those of Botticelli, Vincent van Gogh, and Jackson Pollock. Their visual properties were also explored by mathematicians when Benoit Mandelbrot published The Fractal Geometry of Nature (1982) in which he catalogued nature’s statistical fractals and discussed them using mathematical methods for their replication.

Fractals constitute a central component of human daily experience of the environment (Taylor & Spehar, 2016). While extensive research has documented the negative effects of environments that do not have
a complement of rich experiential aesthetic variety (Mehaffy & Salingaros, 2013), their proliferation in art and design has continued to grow and diversify, creating architecture, interiors and products designed for human needs (Taylor & Spehar, 2016). Over the past two decades, interdisciplinary teams have confirmed that the aesthetic qualities of nature’s fractal patterns can induce striking effects on health.1

PARAMETERS OF FRACTAL PREFERENCE

Source: Working with Fractals: For the Love of Fractals

The universal preference for ‘statistical’ fractals peaks at low to moderate degree of complexity, while universal preference for ‘exact’ fractals peaks at a higher complexity. The high level of symmetry in exact fractals enables greater tolerance for visual complexity compared to statistical fractals (Abboushi et al., 2019). Four factors influence complexity in exact fractals:

1. Fractal dimension (D)

2. Symmetry

3. Recursion

4. Number of elements introduced at each recursion

Fractal dimension. 

The Euclidean simplicity and symmetry of exact fractals increases tolerance and peak preference for medium-high complexity exact fractals (D= 1.5–1.7) (Abboushi et al., 2019). Medium- high exact fractals can enhance visual preference and mood, particularly in less complex Euclidean interior spaces (Abboushi et al., 2019; Taylor et al., 2018).

When complex fractal patterns are experienced within a low-complexity interior space, the visual preference can shift to those available higher D values (1.5 to 1.7, medium-high range), suggesting that a low complexity environment enables a tolerance and preference for higher complexity statistical fractals such as found in artworks or casted light patterns unique within that space (Abboushi et al., 2019). A good example of this scenario is museums with an abundance of geometrical rooms and white walls adorned with highly complex artworks that captivate.

Symmetry. 

Patterns with symmetry and geometry, such as common among exact fractals, can be visually appealing as they balance interest and comprehensibility. Mirror symmetry is generally considered one of the most predictive factors when judging whether a geometric pattern is ‘beautiful’. A lack of radial and mirror symmetry can be overcome by including more recursion and higher fractal dimensionality.

The orderliness of exact fractals allows a pattern to approach the maximum use of space at a particular dimension while retaining its elegance. Patterned tiles and carpet, wall coverings and textiles, artefacts and ornaments found in many cultures (Eglash, 2002) are evidence of this spatial orderliness and symmetry.

Recursion. 

Fractals generated by a finite subdivision rule bear a striking resemblance to both nature and human ornament. In mathematics, the finite subdivision rule is a recursive way of dividing a polygon or other two-dimensional shape into smaller and smaller pieces. In a sense, subdivision rules are generalisations of regular exact fractals. Instead of repeating exactly the same design over and over, they have slight variations in each stage, allowing a richer structure while maintaining the elegant style of fractals (Cannon, et al., 2001).

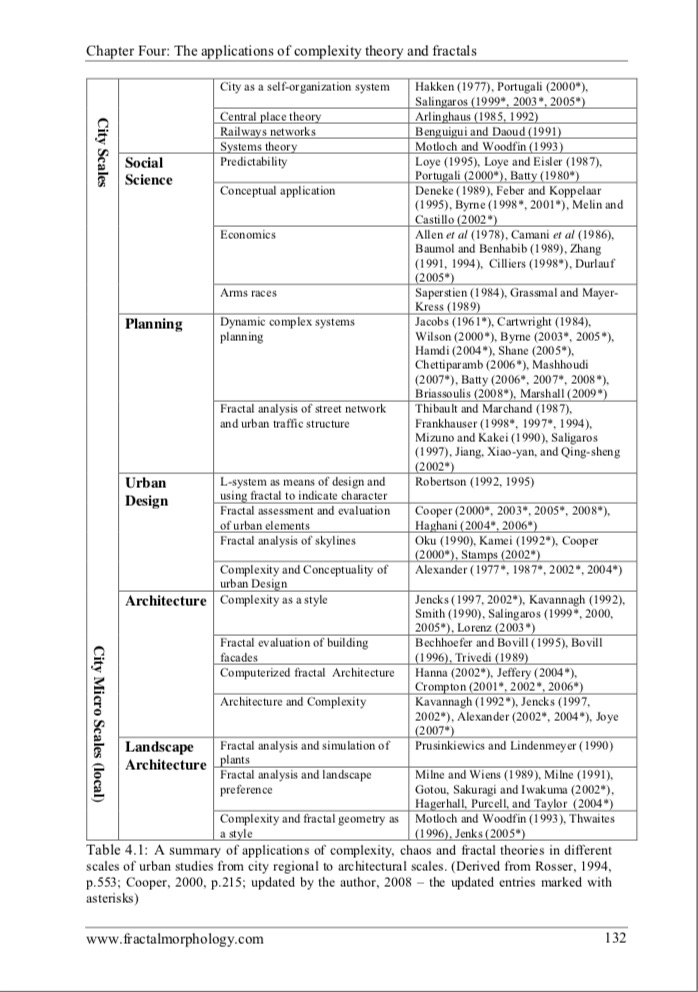
Source: The application of complexity theory and Fractals in architecture, urban planning and design

Source: The application of complexity theory and Fractals in architecture, urban planning and design

My Related Posts

Shapes and Patterns in Nature

Shape of the Universe

Cosmic Mirror Theory

Interconnected Pythagorean Triples using Central Squares Theory

Indra’s Net: On Interconnectedness

The Great Chain of Being

Maha Vakyas: Great Aphorisms in Vedanta

Growth and Form in Nature: Power Laws and Fractals

Geometry of Consciousness

Consciousness of Cosmos: A Fractal, Recursive, Holographic Universe

Mind, Consciousness and Quantum Entanglement

Meta Integral Theories: Integral Theory, Critical Realism, and Complex Thought

From Systems to Complex Systems

The Pillar of Celestial Fire

Key Sources of Research:

Role of Fractal Geometry in Indian Hindu Temple Architecture

Dhrubajyoti Sardar
M.Arch Scholar
Architecture & Planning Department, IIT Roorkee

Roorkee, Uttarakhand, India

S. Y. Kulkarni
Professor & Former Head Architecture & Planning Department, IIT Roorkee Roorkee, Uttarakhand, India

International Journal of Engineering Research & Technology (IJERT) 

ISSN: 2278-0181 Vol. 4 Issue 05, May-2015

Click to access role-of-fractal-geometry-in-indian-hindu-temple-architecture-IJERTV4IS050709.pdf

Physical Fractals: Self Similarity and Square-Integratibility

Akhlesh Lakhtakia

Penn State

Speculations in Science and Technology 18, 153-156, 1995

Click to access No260(SST).PDF

The Hindu Temple as a Model of Fractal Cosmology – Forecasting Architecture with Recursive Instruction

Data is Nature

Monday, 6 April 2015

http://www.dataisnature.com/?p=2138

Dancing Architecture: The parallel evolution of Bharatanātyam and South Indian Architecture

Kavitha Jayakrishnan

University of Waterloo
Master of Architecture Thesis 2011

https://uwspace.uwaterloo.ca/bitstream/handle/10012/6356/Jayakrishnan_Kavitha.pdf?sequence=1

Building Science of Indian Temple Architecture

Shweta Vardia

shwetavardia@gmail.com

2008 MS Thesis

Universidade do Minho, Portugal

Click to access 2008_SVardia.pdf

The Fractal Structure of Hindu Temples

Fractal Enlightenment

https://fractalenlightenment.com/14556/fractals/the-fractal-structure-of-hindu-temples

Fractal Geometry And Self-Similarity In Architecture: An Overview Across The Centuries

Nicoletta Sala
Academy o f Architecture o f Mendrisio, University o f Italian Switzerland Largo Bernasconi CH- 6850 Mendrisio
Switzerland
E-mail: nsala @ arch.unisLch

Click to access bridges2003-235.pdf

Shapes, Patterns and Meanings in Indian Temple Architecture

Tanisha Dutta*, V. S. Adane

Department of Architecture and Planning, Visvesvaraya National Institute of Technology Nagpur, India *Corresponding author: ar.tanisha.dd@gmail.com

Received July 17, 2018; Revised August 20, 2018; Accepted November 05, 2018

American Journal of Civil Engineering and Architecture, 2018, Vol. 6, No. 5, 206-215

Available online at http://pubs.sciepub.com/ajcea/6/5/6 ©Science and Education Publishing DOI:10.12691/ajcea-6-5-6

Click to access ajcea-6-5-6.pdf

Hindu Temple: Models of a Fractal Universe. 

Trivedi, K. (1993).

International Seminar on Mayonic Science and Technology,

243-258.

The Visual Computer 5, 243–258 (1989). https://doi.org/10.1007/BF02153753

https://link.springer.com/article/10.1007/BF02153753#citeas

Click to access Hindu_Temple_Models.pdf

Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

IasefMd Riana Jin-HoParka HyungUk Ahna DongkukChangb

aDepartment of Architecture, Inha University, South Korea

bDepartment of Architecture, Chosun University, South Korea

Received 4 May 2006, Revised 21 July 2006, Accepted 15 January 2007, Available online 23 April 2007.

Building and Environment
Volume 42, Issue 12, December 2007, Pages 4093-4107

Click to access 2007_02.pdf

https://www.sciencedirect.com/science/article/abs/pii/S0360132307000273

https://www.semanticscholar.org/paper/Fractal-geometry-as-the-synthesis-of-Hindu-in-Rian-Park/719b6da37091121786525e4b99a667fb098abf49

Symbolism in Hindu Temple
Architecture through Fractal Geoemtry- ‘Thought Behind Form’.

Dutta, T., & V.S.Adane. (2014).

International Journal of Science and Research (IJSR), 489-497.

Click to access U1VCMTQzMjI=.pdf

https://www.semanticscholar.org/paper/Symbolism-in-Hindu-Temple-Architecture-and-Fractal-Dutta-Adane/891db316ae9b06387a0e23ec4e2df649f43d2cd0

Fractal geometry and architecture: some interesting connections

N. Sala

Accademia di Architettura, Università della Svizzera italiana, Mendrisio, Switzerland

Eco-Architecture: Harmonisation between Architecture and Nature 163

Click to access ARC06017FU1.pdf

Temples of Odisha- the Geometry of Plan Form

Rinku Parashar

Assistant Professor Department of Architecture Engineering NIT, Raipur, 492010, India

Dr Abir Bandyopadhyay

Professor & Head Department of Architecture Engineering NIT, Raipur, 492010, India

IJIRST –International Journal for Innovative Research in Science & Technology| Volume 2 | Issue 10 | March 2016 ISSN (online): 2349-6010

Click to access IJIRSTV2I10036.pdf

Shape and geometrical study of fractal cosmology through Orissan Temple architecture

Partha Sarathi Mishra

january 2013

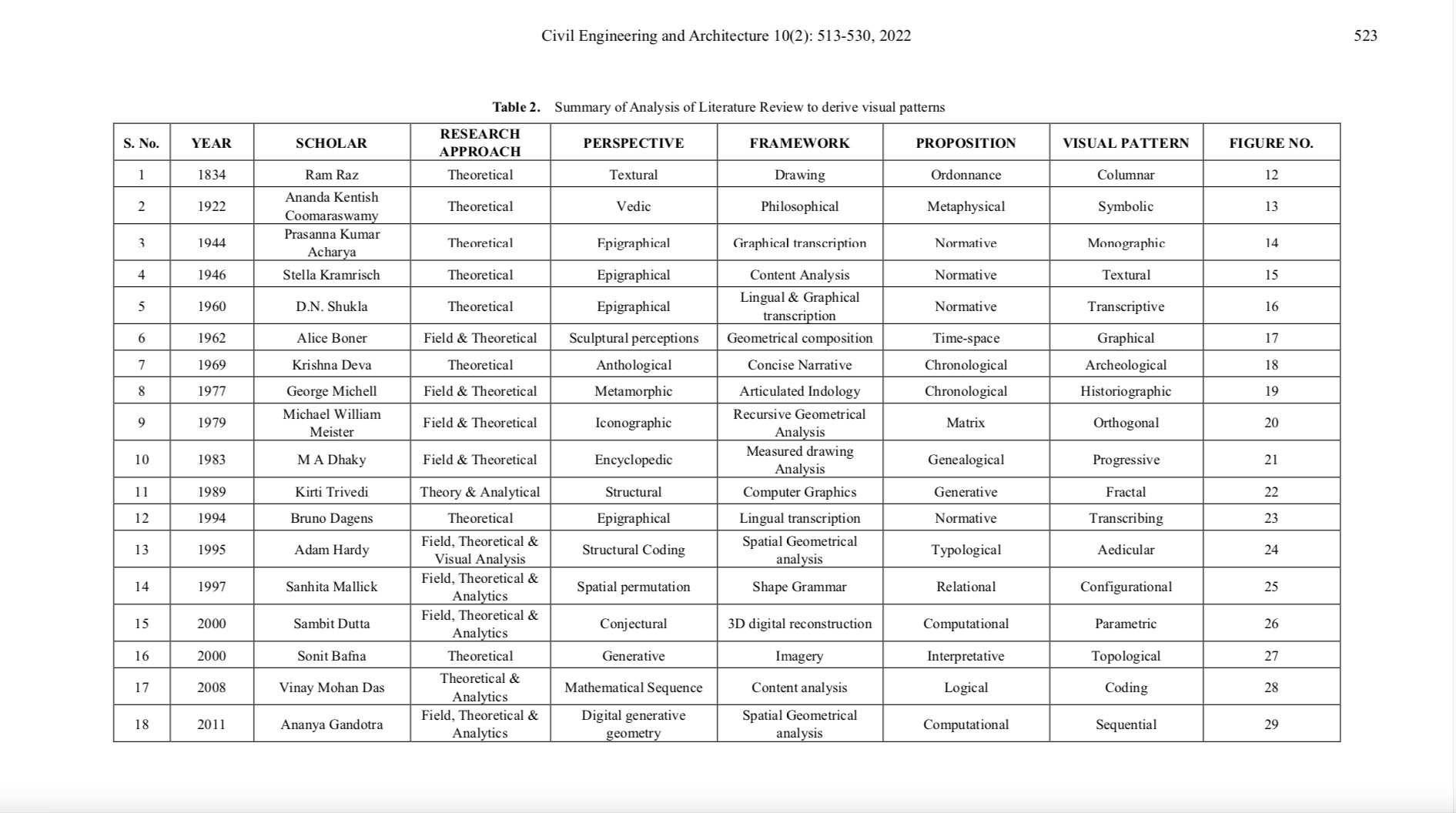
Click to access Shape-and-geometrical-study-of-fractal-cosmology-through-Orissan-Temple-architecture.pdf

“Investigating Architectural Patterns of Indian Traditional Hindu Temples through Visual Analysis Framework,”

Aditya Kumar Singh, Vinay Mohan Das, Yogesh Kumar Garg, Mohammad Arif Kamal ,

Civil Engineering and Architecture, Vol. 10, No. 2, pp. 513-530, 2022.

DOI: 10.13189/cea.2022.100211.

Click to access CEA11-14825255.pdf

https://www.semanticscholar.org/paper/Investigating-Architectural-Patterns-of-Indian-Singh-Das/76b27cc56ba003d899dbc8c0595f304f02e4bb28

“Infinite Sequences in the Constructive Geometry Of Tenth-Century Hindu Temple Superstructures”,

Datta, S.,

School of Architecture and Building Deakin University 1, Gheringhap Street Geelong VIC 3219 AUSTRALIA 

sdatta@deakin.edu.au

Nexus Network Journal – Vol.12, No. 3, 2010 471 – 483

DOI 10.1007/s00004-010-0038-0; published online 15 September 2010
Kim Williams Books, Turin

https://www.semanticscholar.org/paper/Infinite-Sequences-in-the-Constructive-Geometry-Of-Datta/18ed5ec4e6e33a8ebdf5b5c1e6fdc8706b34fdcc

https://link.springer.com/article/10.1007/s00004-010-0038-0

Evolution and Interconnection: Geometry in Early Temple Architecture

DOI:10.1007/978-3-030-57907-4_11

Corpus ID: 238053244

https://www.semanticscholar.org/paper/Evolution-and-Interconnection%3A-Geometry-in-Early-Datta/c767a450532cf281e0bdd0cfac493343c2a2de07

Fractal Geometry as a source of innovative formations in interior design 

Omniah Bahaa Ibrahim

Teaching Assistant, at Faculty of Applied Arts, Interior Design & Furniture Department, Helwan University, Giza, Egypt

DOI: 10.21608/jdsaa.2021.42275.1075

Click to access article_174415_850712616886211291f5a31081befa6e.pdf

Fractal Geometry and Architecture Design: Case Study Review

Xiaoshu Lu1,2, Derek Clements-Croome3, Martti Viljanen1

1Department of Civil and Structural Engineering, School of Engineering, Aalto University, PO Box 12100, FIN-02150, Espoo, Finland
E-mail: xiaoshu@cc.hut.fi
2Finnish Institute of Occupational Health, Finland
3School of Construction Management and Engineering, Whiteknights, University of Reading, PO Box 219, Reading RG6 6AW, UK

Click to access 2_CMSIM_2012_Lu_clements_Croome_viljanen_2_311-322.pdf

A review of the fractal geometry in structural elements

Aman Upadhayay, Dr. Savita Maru
Department of Civil Engineering, Ujjain Engineering College, India

International Journal of Advanced Engineering Research and Science (IJAERS)
Peer-Reviewed Journal
ISSN: 2349-6495(P) | 2456-1908(O)

Vol-8, Issue-7; Jul, 2021
Journal Home Page Available: https://ijaers.com/ 

Article DOI: https://dx.doi.org/10.22161/ijaers.87.3

Click to access 3IJAERS-06202164-Areview.pdf

The fractal analysis of architecture: calibrating the box-counting method using scaling coefficient and grid disposition variables

Michael J Ostwald

School of Architecture and Built Environment, University of Newcastle, University Drive, Callaghan, NSW 2308, Australia;

email: Michael.Ostwald@newcastle.edu.au
Received 15 July 2011; in revised form 21 March 2012

Environment and Planning B: Planning and Design 2013, volume 40, pages 644 – 663 

doi:10.1068/b38124

https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.884.7292&rep=rep1&type=pdf

Mandapa: Its Proportion as a tool in Understanding Indian Temple Architecture

Ragima N Ramachandran

International Journal of Scientific & Engineering Research Volume 10, Issue 7, July-2019 2104 ISSN 2229-5518

Click to access Mandapa-Its-Proportion-as-a-tool-in-Understanding-Indian-Temple-Architecture.pdf

African Fractals

MODERN COMPUTING AND INDIGENOUS DESIGN

RON EGLASH

Book

PARAMETRIZING INDIAN KARNATA-DRAVIDA TEMPLE USING GEOMETRY

SRUSHTI GOUD

BMS School of Architecture, Yelahanka, Bangalore, India

goudsrushti@gmail.com

Click to access ascaad2016_042.pdf

A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE

PRATHAMESH GURME1,PROF. UDAY PATIL2

1UG SCHOLAR,2HEAD OF DEPARTMENT, DEPARTMENT OF CIVIL ENGINEERING BHARATI VIDHYAPEETH’S COLLEGE OF ENGINEERING , LAVALE , PUNE , INDIA

INTERNATIONAL JOURNAL FOR RESEARCH & DEVELOPMENT IN TECHNOLOGY

Click to access 2133138-A%20REVIEW%20STUDY%20ON%20ARCHITECTURE%20OF%20HINDU%20TEMPLE.pdf

Exploring Ancient Architectural Designs with Cellular Automata

Hokky Situngkir
[hokky.situngkir@surya.ac.id]
Dept. Computational Sociology, Bandung Fe Institute Center for Complexity Studies in Surya University

BFI Working Paper Series WP-9-2010

Click to access 1508.03610.pdf

WORKING WITH FRACTALS

A RESOURCE FOR PRACTITIONERS OF BIOPHILIC DESIGN

A PROJECT OF THE EUROPEAN ‘COST RESTORE ACTION’ 

PREPARED BY RITA TROMBIN

Click to access Working-with-Fractals-by-Rita-Trombin_v2021-06-21_TBG-COST-RESTORE.pdf

The application of complexity theory and Fractals

in architecture, urban planning and design

Click to access finalCh4.pdf

Chapters

http://www.toofanhaghani.com

The influence of traditional Indian architecture in Balkrishna Doshi’s IIM Complex at Bangalore: A comparative analysis using fractal dimensions and lacunarity

,Mario Lodeweik LIONAR,  (Ph.D. Program of Architecture, Institute of Natural Sciences, Bursa Uludağ University, Bursa, Turkey) 

Özgür Mehmet EDİZ (Department of Architecture, Faculty of Architecture, Bursa Uludağ University, Bursa, Turkey) 

A|Z ITU Mimarlık Fakültesi Dergisi 

DOI: 10.5505/itujfa.2021.80388

https://search.trdizin.gov.tr/yayin/detay/503974/

The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry

Nelly Shafik Ramzy 

Sinai University

Peregrinations: Journal of Medieval Art and Architecture

Volume 5 Issue 2 2015

Click to access 235442558.pdf

PRINCIPLES OF FRACTAL GEOMETRY AND APPLICATIONS IN ARCHITECTURE AND CIVIL ENGINEERING

Anton Vrdoljak, M.Sc.
Faculty of Civil Engineering, University of Mostar, anton.vrdoljak@gf.sum.ba Kristina Miletić, B.Sc.(Math.)
Faculty of Civil Engineering, University of Mostar, kristina.miletic@gf.sum.ba

Number 17, June 2019.

https://hrcak.srce.hr/file/324620

SHAPE AND GEOMETRY OF ORISSAN TEMPLE ARCHITECTURE

Authors: Mishra, Partha Sarathi

MS Thesis, IITR 2012

http://localhost:8081/xmlui/handle/123456789/2017

http://shodhbhagirathi.iitr.ac.in:8081/jspui/handle/123456789/2017

The Shape of Cities: Geometry, Morphology, Complexity and Form

Chapter in book Fractal Cities

Click to access 1370661_Fractal%20Cities%20Chapter%201.pdf

WHOLENESS, VISUAL COMPLEXITY AND MATERIALITY:

A Comparative Analysis Using Fractal Dimension Analysis And Mirror Of The Self-Test In The Case Of Material Imitations.

author | FILIP KINNERT supervisor | doc. PhDr. MARTIN HORÁČEK Ph.D.

Click to access KINNERT-ACAU21-POSTER-211007.pdf


Vastu Purusha Mandala – A human ecological framework for designing living environments.

Venugopal, Jayadevi

In Jetty, C, Chandra, B, Bhashyam, A, & Prabhakara, R (Eds.) Proceedings of International Conference on Advances in Architecture and Civil Engineering (AARCV 2012), Volume 2.
Bonfring, India, pp. 870-877.

Click to access VPM_framework_Jayadevi.pdf

Rediscovering the Hindu Temple:
The Sacred Architecture and Urbanism of India

Vinayak Bharne and Krupali Krusche

Book, ISBN (10): 1-4438-4137-4, ISBN (13): 978-1-4438-4137-5

Click to access 978-1-4438-4137-5-sample.pdf

Borobudur was Built Algorithmically

Hokky Situngkir

[hs@compsoc.bandungfe.net]

Dept. Computational Sociology Bandung Fe Institute

Click to access 2010h.pdf

TEMPLE ARCHITECTURE AND SCULPTURE

NCERT

Click to access kefa106.pdf

Fractal Cities: A Geometry of Form and Function,

Batty, M., Longly, P., 1994, 

Academic Press, San Diego.

Book

Space and Cosmology in the Hindu Temple

Subhash Kak

Presented at Vaastu Kaushal: International Symposium on Science and Technology in Ancient Indian Monuments, New Delhi, November 16-17, 2002.

Click to access Time2.pdf

Gender and space in temple architecture

D. Midhila

midhilachandra@gmail.com

Hindustan Institute of Technology and Sciences, Vijayawada, Andhra Pradesh

Dr. R. V. Nagarajan

rvnagarajan@hindustanuniv.ac.in

Hindustan Institute of Technology and Sciences, Padur, Chennai, Tamilnadu

International Journal of Advance Research, Ideas and Innovations in Technology

2020

Click to access V6I4-1158.pdf

The Role of Five Elements of Nature In Temple Architecture 

Ar. Snigdha Chaudhary

International Journal of Scientific & Engineering Research Volume 8, Issue 7, July-2017 1149 ISSN 2229-5518

Click to access The-Role-of-Five-Elements-of-Nature-In-Temple-Architecture.pdf

Trends in Fractal Dimension in Laxman and Kandariya Mahadev Temples, Khajuraho

Tanisha Dutta1,* and Vinayak S. Adane2

1Phd Research Scholar, Department of Architecture and Planning, Visvesvaraya National Institute of Technology, Nagpur- 440010, India.

2Professor, Department of Architecture and Planning, Visvesvaraya National Institute of Technology, Nagpur- 440010, India. (*Corresponding author)

nternational Journal of Applied Engineering Research ISSN 0973-4562 Volume 13, Number 3 (2018) pp. 1728-1741

© Research India Publications. http://www.ripublication.com

Click to access ijaerv13n3_27.pdf

Hindu Temple Fractals

William J Jackson

https://www.academia.edu/347639/Hindu_Temple_Fractals

Indian Architectural Theory: Contemporary Uses of Vastu Vidya

Vibhuti Chakrabarti

Oxford University Press (1999)

ISBN 0195650417

Maṇḍala in Architecture: Symbolism and Significance for Contemporary Design Education in India

Navin Piplani Ansal University India

Tejwant Singh Brar Ansal University India

IAFOR Journal of Education: Studies in Education

Volume 8 – Issue 4 – 2020

Click to access EJ1279443.pdf

The Intriguing Temples of the 64 Yoginis

2022

The intriguing temples of the 64 Yoginis

Networks, Narratives, and Interaction

Networks, Narratives, and Interaction

Bruner (1973: xi) described this duality as follows:“our knowledge of the world is not merely a mirroring or reflection of order and structure ‘out there,’ but consists rather of a construct or model that can, so to speak, be spun a bit ahead of things to predict how the world will be or might be”

Key Terms

  • Narratives
  • Culture
  • Psychology
  • Anthropology
  • Meaning
  • Meaning making
  • Networks
  • Boundaries
  • Folk Culture
  • Communication
  • Sensemaking
  • Active Learning
  • Karl Weick
  • Dirk Baecker
  • Jerome Bruner
  • Erving Goffman
  • George Spencer Brown
  • Charles Sanders Peirce
  • Social Interactions
  • Strategic Interactions
  • Cultural Psychology
  • Systems
  • Social Systems
  • Individual and Collective
  • Symbolic Interactions
  • Face Work
  • Face to Face
  • Micro Sociology
  • Drama
  • Kenneth Burke
  • Chain of Events
  • Sequence of Events
  • Time Space
  • Choices, Conflicts, Dilemmas
  • Constraints, Limits, Boundaries
  • Networks, Connections, Interaction
  • Social Simulation
  • Discrete Events
  • Scenes, Scenarios
  • Games and Dramas
  • Harmony
  • Colors, Tones
  • Interaction Rituals
  • Interaction Order
  • Ethnomethodology
  • LL and LR Quadrants in AQAL Model of Ken Wilber
  • Many Faces of Man
  • Backstage and Frontstage
  • Russell Ackoff’s Interaction Planning
  • Faces, Masks, and Rituals
  • Frame Analysis
  • Self and Others
  • Social Constructivism
  • Agent Based Modeling
  • Cellular Automata
  • Computational Sociology
  • Micro Motives and Macro Behavior
  • Conversations
  • Strategic Conversations
  • Boundaries and Distinctions
  • Networks and Boundaries

Jerome Bruner ON Narratives

Source: Chapter 1 Narrative Inquiry: From Story to Method

… Narrative as a mode of knowing …

In 1984 at an address to the annual meeting of the American Psychological Association, Jerome Bruner challenged the psychological community to consider the possibilities of narrative as one of two distinct and distinctive modes of thinking, namely the “paradigmatic” or logico-scientific mode and the narrative mode. For Bruner, each mode constituted a unique way of construing and constructing reality and of ordering experience. Importantly, neither of these modes was reducible to the other, as each was necessary in the development of human thought and action. Taking up these ideas in later writings, Bruner (1986) presents the narrative mode of meaning-making as one that “looks for particular conditions and is centred around the broader and more inclusive question of the meaning of experience” (p. 11), whilst the paradigmatic mode is characterised as one that is more concerned with establishing universal truth conditions.

Bruner has pursued the notion of “narrative” modes of thinking and explored the ways in which we draw on “narrative” modes of knowing as a learning process (1996a). For Bruner, we construct our understandings of the world “mainly in the form of narrative – stories, excuses, myths, reasons for doing and not doing, and so on” (2003, p. 44). In earlier writings, he points to the power and import of narrative as a meaning-making process, commenting that “our capacity to render experience in terms of narrative is not just child’s play, but an instrument for making meaning that dominates much of life in culture – from soliloquies at bedtime to the weighing of testimony in our legal system” (1990, p. 97). Importantly, Bruner suggests that our “sensitivity” to narrative constitutes a major link between our “sense of self and our sense of others in the social world around us” (1986, p. 69) and is the mode through which we “create a version of the world” with which we can live (1996a, p. 39).

Bruner’s work in the field of cognitive psychology constitutes one way in which narrative has been conceptualised within scholarship and has led to the establishment of the field of narrative psychology. It is perhaps serendipitous that Bruner’s account of the narrative mode of thinking occurred at a time of growing interest in the ways in which narrative might be drawn upon for research and inquiry purposes. As educators and scholars took up the “call of stories” (Coles, 1989) to provide alternative means to explore, interrogate, interpret, and record experience, “it helped that the messenger was Bruner, an enormously powerful scholar with unusual cross-disciplinary knowledge, stature, and impact, who ventured to articulate what narrative could mean to the social sciences at large” (Bresler, 2006, p. 23). Crucially, Bruner’s work leads us to consider narrative as more than a means of presenting meaning and to consider the role of narrative and narrative forms in “re-presenting,” in the sense of constructing meaning, both individually and collectively. For Bruner, narrative operates simultaneously in both thought and action, shaping the ways in which we conceive and respond to our worlds. In short, all cognition, whatever its nature, relies upon representation, how we lay down our knowledge in a way to represent our experience of the world . . . representation is a process of construction, as it were, rather than of mere reflection of the world (Bruner, 1996b, p. 95).

Here, a narrative might become a “template for experience” (Bruner, 2002, p. 34) that works on the mind, modelling “not only its world but the minds seeking to give it its meanings” (p. 27). This move from narrative as “story presented” to narrative as a “form of meaning-making,” indeed, a form of “mind-making,” has played an important role in the development of narrative as a method of inquiry in the social sciences.

Source: INTRODUCTION: BRUNER’S WAY/ David Bakhurst and Stuart G. Shanker

Another reason why Bruner is an ideal focus is his role in two crucial paradigm shifts in twentieth-century psychology. In the 1950s, he was an instrumental figure in the cognitive revolution, which restored to psychology the inner life of the mind after decades of arid behaviourist objectivism. Cognitive psychology prospered and, in league with other fields, evolved into ‘cognitive science’, conceived as a systematic inter- disciplinary approach to the study of mind (see Gardner, 1985). Bruner, however, gradually grew more and more dissatisfied with what cognitivism had become. In 1990, he published Acts of Meaning, in which he argued that the cognitive revolution had betrayed the impulse that had brought it into being. The revolution’s principal concern, Bruner argued, had been to return the concept of meaning to the forefront of psychological theorizing. But cognitivism had become so enamoured of computational models of the mind that it had replaced behaviourism’s impoverished view of the person with one no better: human beings as information processors. In response, Bruner argued forcefully that meaning is not a given, but something made by human beings as they negotiate the world. Meaning is a cultural, not computational, phenomenon. And since meaning is the medium of the mental, culture is constitutive of mind.

In many ways, Bruner’s objection was familiar. It had often been lamented that mainstream psychology was individualistic and scientistic, representing minds as self-contained mental atoms and ignoring the social and cultural influences upon them. In the last decade, however, this well-known critique has really been gaining momentum. Besides Bruner, both Richard Shweder (1990) and Michael Cole (1996) have sounded the call for a new ‘cultural psychology’. Assorted versions of ‘constructionist’ and ‘discursive’ psychology have appeared on the scene, joining a veritable chorus of diverse voices urging that psychology treat the mind as a sociocultural phenomenon (e.g., Edwards and Potter, 1992; Harré and Gillett, 1994; Gergen, 1999). It is particularly striking that these voices no longer come exclusively from the margins. Just as the left/right divide is collapsing in political theory, so the dichotomy between mainstream ‘individualistic/scientistic/Cartesian’ psychology and radical ‘communitarian/interpretative/post-Cartesian’ psychology has become outmoded. Cognitive scientists and philosophers of mind now commonly acknowledge that no plausible account of the mind can be indifferent to the context in which we think and act, and some significant works have appeared devoted to the cultural origins, and social realization, of human mentality (e.g., Donald, 1991). A psychologist interested in culture is no longer a counter-cultural figure.

Source: The narrative constitution of identity: A relational and network approach

From diverse sources it is possible to identify four features of a reframed narrativity particularly relevant for the social sciences:1) relationality of parts, 2) causal emplotment, 3) selective appropriation, and 4) temporality, sequence and place.43 Together, these dimensions suggest narratives are constellations of relationships (connected parts) embedded in time and space, constituted by causal emplotment. Unlike the attempt to produce meaning by placing an event in a specified category, narrativity precludes sense making of a singular isolated phenomenon. Narrativity demands that we discern the meaning of any single event only in temporal and spatial relationship to other events. Indeed, the chief characteristic of narrative is that it renders understanding only by connecting (however unstably) parts to a constructed configuration or a social network of relationships (however incoherent or unrealizable) composed of symbolic, institutional, and material practices 4.4

Source: CHAPTER 2 SELF-MAKING AND WORLD-MAKING

Narrative accounts must have at least two characteristics. They should center upon people and their intentional states: their desires, beliefs, and so on; and they should focus on how these intentional states led to certain kinds of activities. Such an account should also be or appear to be order preserving, in the sense of preserving or appearing to preserve sequence — the sequential properties of which life itself consists or is supposed to consist. Now, in the nature of things, if these points are correct, autobiographies should be about the past, should be par excellence the genre (or set of genres) composed in the past tense. So just for fun, we decided to find out whether in fact autobiographies were all in the past tense — both the spontaneous ones we had collected and a sample of literary autobiographies.

We have never found a single one where past-tense verbs constituted more than 70 percent of the verbs used. Autobiographies are, to be sure, about the past; but what of the 30 percent or more of their sentences that are not in the past tense? I’m sure it will be apparent without all these statistics that autobiography is not only about the past, but is busily about the present as well. If it is to bring the protagonist up to the present, it must deal with the present as well as the past — and not just at the end of the account, as it were. That is one part of it. But there is another part that is more interesting. Most of the “present-tense” aspect of autobiography has to do with what students of narrative structure call “evaluation” — the task of placing those sequential events in terms of a meaningful context. Narrative, whether looked at from the more formalistic perspective of William Labov (1982) or the more literary, historical one of Barbara Herrnstein-Smith (1986), necessarily comprises two features: one of them is telling what happened to a cast of human beings with a view to the order in which things happened. That part is greatly aided by the devices of flashback, flashforward, and the rest. But a narrative must also answer the question “Why”, “Why is this worth telling, what is interesting about it?” Not everything that happened is worth telling about, and it is not always clear why what one tells merits telling. We are bored and offended by such accounts as“I got up in the morning, got out of bed, dressed and tied my shoes, shaved, had breakfast, went off to the office and saw a graduate student who had an idea for a thesis…”

The “why tell” function imposes something of great (and hidden) significance on narrative. Not only must a narrative be about a sequence of events over time, structured comprehensibly in terms of cultural canonicality, it must also contain something that endows it with exceptionality. We had better pause for a moment and explore what this criterion of exceptionality means for autobiography and, incidentally, why it creates such a spate of present-tense clauses in the writing of autobiography.

Source: CHAPTER 2 SELF-MAKING AND WORLD-MAKING

The object of narrative, then, is to demystify deviations. Narrative solves no problems. It simply locates them in such a way as to make them comprehensible. It does so by invoking the play of psychological states and of actions that transpire when human beings interact with each other and relates these to what can usually be expected to happen. I think that Kenneth Burke has a good deal to say about this “play of psychological states” in narrative, and I think it would help to examine his ideas. In his The Grammar of Motives, he introduces the idea of “dramatism” (Burke 1945). Burke noted that dramatism was created by the interplay of five elements (he refers to them as the Pentad). These comprise an Actor who commits an Action toward a Goal with the use of some Instrument in a particular Scene. Dramatism is created, he argues, when elements of the Pentad are out of balance, lose their appropriate “ratio”. This creates Trouble, an emergent sixth element. He has much to say about what leads to the breakdown in the ratios between the elements of the dramatistic pentad. For example, the Actor and the Scene don’t fit. Nora, for example: what in the world is the rebellious Nora in A Doll’s House doing in this banal doctor’s household? Or Oedipus taking his mother Jocasta unknowingly to wife. The “appropriate ratios”, of course, are given by the canonical stances of folk psychology toward the human condition. Dramatism constitutes their patterned violation. In a classically oral culture, the great myths that circulate are the archetypal forms of violation, and these become increasingly “smoothed” and formalized — even frozen — over time, as we know from the classic studies of Russian folktales published by Vladimir Propp (1986). In more mobile literary cultures, of course, the range and variation in such tales and stories greatly increases, matching the greater complexity and widened opportunities that accompany literacy. Genres develop, new forms emerge, variety increase — at least at first. It may well be that with the emergence of mass cultures and the new massifying media, new constraints on this variation occur, but that is a topic that would take us beyond the scope of this essay (see Feldman, in this volume).

Erving Goffman On Interactionism

Source: Wikipedia

Goffman was influenced by Herbert Blumer, Émile Durkheim, Sigmund Freud, Everett Hughes, Alfred Radcliffe-Brown, Talcott Parsons, Alfred Schütz, Georg Simmel and W. Lloyd Warner. Hughes was the “most influential of his teachers”, according to Tom Burns.[1][3][22] Gary Alan Fine and Philip Manning have said that Goffman never engaged in serious dialogue with other theorists,[1] but his work has influenced and been discussed by numerous contemporary sociologists, including Anthony Giddens, Jürgen Habermas and Pierre Bourdieu.[23]

Though Goffman is often associated with the symbolic interaction school of sociological thought, he did not see himself as a representative of it, and so Fine and Manning conclude that he “does not easily fit within a specific school of sociological thought”.[1] His ideas are also “difficult to reduce to a number of key themes”; his work can be broadly described as developing “a comparative, qualitative sociology that aimed to produce generalizations about human behavior”.[23][24]

Goffman made substantial advances in the study of face-to-face interaction, elaborated the “dramaturgical approach” to human interaction, and developed numerous concepts that have had a massive influence, particularly in the field of the micro-sociology of everyday life.[23][25] Much of his work was about the organization of everyday behavior, a concept he termed “interaction order”.[23][26][27] He contributed to the sociological concept of framing (frame analysis),[28] to game theory (the concept of strategic interaction), and to the study of interactions and linguistics.[23] With regard to the latter, he argued that the activity of speaking must be seen as a social rather than a linguistic construct.[29] From a methodological perspective, Goffman often employed qualitative approaches, specifically ethnography, most famously in his study of social aspects of mental illness, in particular the functioning of total institutions.[23] Overall, his contributions are valued as an attempt to create a theory that bridges the agency-and-structuredivide—for popularizing social constructionism, symbolic interaction, conversation analysis, ethnographic studies, and the study and importance of individual interactions.[30][31] His influence extended far beyond sociology: for example, his work provided the assumptions of much current research in language and social interaction within the discipline of communication.[32]

Goffman defined “impression management” as a person’s attempts to present an acceptable image to those around them, verbally or nonverbally.[33] This definition is based on Goffman’s idea that people see themselves as others view them, so they attempt to see themselves as if they are outside looking in.[33] Goffman was also dedicated to discovering the subtle ways humans present acceptable images by concealing information that may conflict with the images for a particular situation, such as concealing tattoos when applying for a job in which tattoos would be inappropriate, or hiding a bizarre obsession such as collecting/interacting with dolls, which society may see as abnormal.

Goffman broke from George Herbert Mead and Herbert Blumer in that while he did not reject the way people perceive themselves, he was more interested in the actual physical proximity or the “interaction order” that molds the self.[33] In other words, Goffman believed that impression management can be achieved only if the audience is in sync with a person’s self-perception. If the audience disagrees with the image someone is presenting then their self-presentation is interrupted. People present images of themselves based on how society thinks they should act in a particular situation. This decision how to act is based on the concept of definition of the situation. Definitions are all predetermined and people choose how they will act by choosing the proper behavior for the situation they are in. Goffman also draws from William Thomas for this concept. Thomas believed that people are born into a particular social class and that the definitions of the situations they will encounter have already been defined for them.[33] For instance. when an individual from an upper-class background goes to a black-tie affair, the definition of the situation is that they must mind their manners and act according to their class.

In 2007 by The Times Higher Education Guide listed Goffman as the sixth most-cited author in the humanities and social sciences, behind Anthony Giddens and ahead of Habermas.[2] His popularity with the general public has been attributed to his writing style, described as “sardonic, satiric, jokey”,[31] and as “ironic and self-consciously literary”,[34] and to its being more accessible than that of most academics.[35] His style has also been influential in academia, and is credited with popularizing a less formal style in academic publications.[31] Interestingly, if he is rightly so credited, he may by this means have contributed to a remodelling of the norms of academic behaviour, particularly of communicative action, arguably liberating intellectuals from social restraints unnatural to some of them.

His students included Carol Brooks Gardner, Charles Goodwin, Marjorie Goodwin, John Lofland, Gary Marx, Harvey Sacks, Emanuel Schegloff, David Sudnow and Eviatar Zerubavel.[1]

Despite his influence, according to Fine and Manning there are “remarkably few scholars who are continuing his work”, nor has there been a “Goffman school”; thus his impact on social theory has been simultaneously “great and modest”.[30] Fine and Manning attribute the lack of subsequent Goffman-style research and writing to the nature of his style, which they consider very difficult to duplicate (even “mimic-proof”), and also to his subjects’ not being widely valued in the social sciences.[3][30] Of his style, Fine and Manning remark that he tends to be seen either as a scholar whose style is difficult to reproduce, and therefore daunting to those who might wish to emulate it, or as a scholar whose work was transitional, bridging the work of the Chicago school and that of contemporary sociologists, and thus of less interest to sociologists than the classics of either of those groups.[24][30] Of his subjects, Fine and Manning observe that the topic of behavior in public places is often stigmatized as trivial and unworthy of serious scholarly attention.[30]

Nonetheless, Fine and Manning note that Goffman is “the most influential American sociologist of the twentieth century”.[36] Elliott and Turner see him as “a revered figure—an outlaw theorist who came to exemplify the best of the sociological imagination”, and “perhaps the first postmodern sociological theorist”.[14]

Source: Looking back on Goffman: The excavation continues

The “descent of the ego,” then, was witnessed by both Durkheim and Goffman in terms of the mechanisms at work in modem Western society whereby the tendencies toward an unbridled egoistic individualism are continually rebuffed (Chriss, 1993). MacCannell successfully makes the case for such a Durkheim-Goffman link through a semiotic sociology which resists the temptation of explaining in solely positivistic terms why it is that in modem Western society, imbued as it is with a strong ethic of individualism, we nevertheless see persons orienting their actions toward a perceived moral universe and the accommodation of the other. Like Durkheim and many of the great students of society from Plato to Hobbes, from Kant to Parsons, Goffman was ultimately concerned with the question, how is social order possible (Berger, 1973: 356; Collins, 1980: 173)?

Burns recognizes the Durkheim-Goffman link as well, but carries the analysis even further by comparing and contrasting Durkheim’s notion of social order with Goffman’s interaction order. Durkheim’s sui generis reality was society; Goffman’s is the encounters between individuals, or the social act itself. The moral order which pervades society and sustains individual conduct constitutes a “social fact” in both Durkheim’s and Goffman’s eyes. But Burns (1992) notes also that for Durkheim this order was·seen as durable and all-sustaining, whereas for Goffman “it was fragile, impermanent, full of unexpected holes, and in constant need of repair” (p.26).

my Related Posts

Boundaries and Relational Sociology

Boundaries and Distinctions

Boundaries and Networks

Society as Communication: Social Systems Theory of Niklas Luhmann

Third and Higher Order Cybernetics

Autocatalysis, Autopoiesis and Relational Biology

Relational Turn in Economic Geography

Cybernetics, Autopoiesis, and Social Systems Theory

Truth, Beauty, and Goodness: Integral Theory of Ken Wilber

Systems and Organizational Cybernetics

A Unifying Model of Arts

Ratio Club: A Brief History of British Cyberneticians

Micro Motives, Macro Behavior: Agent Based Modeling in Economics

On Holons and Holarchy

Reflexivity, Recursion, and Self Reference

The Social Significance of Drama and Narrative Arts

Socio-Cybernetics and Constructivist Approaches

Drama Therapy: Self in Performance

Narrative Psychology: Language, Meaning, and Self

Psychology of Happiness: Value of Storytelling and Narrative Plays

Drama Theory: Choices, Conflicts and Dilemmas

Drama Theory: Acting Strategically

Key Sources of Research

The Oxford Handbook of Culture and Psychology

edited by Jaan Valsiner

Culture in Mind: Cognition, Culture, and the Problem of Meaning

By Bradd Shore

Erving Goffman on Wikipedia

https://en.wikipedia.org/wiki/Erving_Goffman

On Face-Work
An Analysis of Ritual Elements in Social Interaction

Erving Goffman
Pages 213-231 | Published online: 08 Nov 2016
https://doi.org/10.1080/00332747.1955.11023008

Chapter in Book Interaction Ritual: Essays on Face to Face Behavior

https://www.tandfonline.com/doi/abs/10.1080/00332747.1955.11023008

Click to access Goffman,%20Erving%20%27On%20Face-work%27.pdf

Click to access GoffmanFace1967.pdf

Interaction Ritual: Essays on Face-To-Face Behavior

E. Goffman

Published 1967

https://www.semanticscholar.org/paper/Interaction-Ritual%3A-Essays-on-Face-To-Face-Behavior-Goffman/976f5fcc01b26ec011790d419eb471eb7beb13f8

 

Encounters: Two Studies in the Sociology of Interaction.

Goffman, Erving. 1961

Indianapolis: Bobbs-Merrill.

The Presentation of Self in Everyday Life. 

Goffman, Erving. 1959. 

New York: Doubleday Anchor.

Strategic interaction.

Goffman, Erving (1969), 

Philadelphia: University of Pennsylvania.

Frame analysis: An essay on the organization of experience.

Goffman, E. (1974). 

New York: Harper & Row.

Sociology. Narrative psychology: Internet and resource guide. 

Hevern, V. W. (2004, Apr). 

Retrieved [3/15/2021] from the Le Moyne College Web site: http://web.lemoyne.edu/~hevern/nr-soc.html

http://web.lemoyne.edu/~hevern/narpsych/nr-soc.html

Narrative scenarios: Toward a culturally thick notion of narrative. 

Brockmeier, J. (2012). 

In J. Valsiner (Ed.), Oxford library of psychology. The Oxford handbook of culture and psychology (p. 439–467). Oxford University Press.

https://psycnet.apa.org/record/2012-04461-020

Erving Goffman

https://monoskop.org/Erving_Goffman

Looking back on Goffman: The excavation continues

James J. Chriss 

Cleveland State University

1993

Sociology & Criminology Faculty Publications. 98.
https://engagedscholarship.csuohio.edu/clsoc_crim_facpub/98

https://engagedscholarship.csuohio.edu/cgi/viewcontent.cgi?article=1099&context=clsoc_crim_facpub

Beyond Goffman: Studies on Communication, Institution, and Social Interaction

1990

Erving Goffman: Exploring,the interaction order 

(1988)

Tom Burns’s Erving Goffman

(1992)

Chapter 1
Narrative Inquiry: From Story to Method

Troubling Certainty

Margaret S. Barrett and Sandra L. Stauffer

In Narrative Inquiry in Music Education

DOI 10.1007/978-1-4020-9862-8  

Springer Science+Business Media B.V. 2009

INTRODUCTION: BRUNER’S WAY

David Bakhurst and Stuart G. Shanker

In Jerome Bruner: Language, Culture, Self

Edited by
David Bakhurst and Stuart G. Shanker

Sage Publications, 2001

Analyzing Narratives and Story-Telling

Matti Hyvärinen

THE SAGE HANDBOOK OF SOCIAL RESEARCH METHODS

Click to access Analyzing-Narratives-and-Story-Telling.pdf

The narrative constitution of identity: A relational and network approach

MARGARET R. SOMERS

Universityof Michigan

TheoryandSociety23: 605-649, 1994

https://deepblue.lib.umich.edu/bitstream/handle/2027.42/43649/11186_2004_Article_BF00992905.pdf?sequence=1

Cognitive–Linguistic and Constructivist Mnemonic Triggers in Teaching Based on Jerome Bruner’s Thinking

Jari Metsämuuronen1* and Pekka Räsänen2

  • 1Department of Pedagogy, NLA University College, Bergen, Norway
  • 2Niilo Mäki Institute, Jyväskylä, Finland

Front. Psychol., 12 December 2018 | https://doi.org/10.3389/fpsyg.2018.02543

https://www.frontiersin.org/articles/10.3389/fpsyg.2018.02543/full

Storytelling and the Construction of Realities

Paul Stoller

Etnofoor Vol. 30, No. 2, Race-ism (2018), pp. 107-112 

The Construction of Identity in the Narratives of Romance and Comedy

Kevin Murray 

Texts of Identity In J.Shotter & K.Gergen (eds.)  London: Sage (1988)

The Construction of Identity in the Narratives of Romance and Comedy

Actual Minds, Possible Worlds

By Jerome S. BRUNER

The Narrative Construction of Reality

Jerome Bruner

Click to access Bruner_Narrative.pdf

Jerome Bruner Life as a Narrative

Click to access Bruner_J_LifeAsNarrative.pdf

Polarising narrative and paradigmatic ways of knowing: exploring the spaces through narrative, stories and reflections of personal transition

CLEO91571

David Cleaver

cleaver@usq.edu.au University of Southern Queensland

Click to access 11040168.pdf

Possibilities for Action: Narrative Understanding

Donald Polkinghorne

Fielding Graduate University

https://journals.lib.unb.ca/index.php/NW/article/view/23789/27568

Two Modes of Thought

Jerome Bruner

Click to access Bruner-Jerome-Two-Modes-of-Thought_excerpt.pdf

Narrating the Self

http://www.sscnet.ucla.edu/anthro/faculty/ochs/articles/96narr_self.pdf?q=narrating-the-self

THE USES OF NARRATIVE IN ORGANIZATION RESEARCH

Barbara Czarniawska

Click to access GRI-rapport-2000-5.pdf

Acts of meaning. 

Bruner, J. (1990). 

Cambridge, MA: Harvard University Press.

Language learner stories and imagined identities

Margaret Early and Bonny Norton
Department of Language and Literacy Education, University of British Columbia

Click to access Early%20and%20Norton%20NI%202011.pdf

Narrative Rhetorics in Scenario Work: Sensemaking and Translation

Zhan Li
University of Southern California USA

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.431.411&rep=rep1&type=pdf

Chapter 2
Self-making and world-making

Jerome Bruner

In Narrative and Identity

Studies in Autobiography, Self and Culture

Jens Brockmeier
University of Toronto & Freie Universität Berlin

Donal Carbaugh
University of Massachusetts at Amherst

John Benjamins Publishing Company

A Grammar of Motives

By Kenneth Burke

Essays Toward a Symbolic of Motives, 1950–1955

By Kenneth Burke

A RHETORIC OF MOTIVES

Kenneth Burke

Click to access CaricatureofCourtshipKafkaCastleKennethBurke.pdf

A Calculus of Negation in Communication

Cybernetics & Human Knowing 24, 3–4 (2017), 17–27

Posted: 23 Jan 2018

Dirk Baecker

Witten/Herdecke University

Date Written: September 1, 2017

https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3102888

Working the Form: George Spencer-Brown and the Mark of Distinction*

Dirk Baecker

Universität Witten/Herdecke

dirk.baecker@uni-wh.de

Click to access workingtheform2.pdf

Shape of things to come: From the ‘laws of form’ to management in the post-growth economy

André Reichel

http://www.ephemerajournal.org volume 17(1): 89-118

Click to access 17-1reichel.pdf

Systems, Network, and Culture

Dirk Baecker Zeppelin University Friedrichshafen, Germany baecker@mac.com

Presented at the International Symposium “Relational Sociology: Transatlantic Impulses for the Social Sciences”, Berlin, September 25-26, 2008

Click to access baecker2.pdf

Organisations as distinction generating and processing systems: Niklas Luhmann’s contribution to organisation studies

David Seidl and Kai Helge Becker

Click to access SeidlandBeckereditedV.pdf

SOCIAL SYSTEMS

Niklas Luhmann
TRANSLATED BY John Bednarz, Jr., with Dirk Baecker FOREWORD BY Eva M. Knodt
STANFORD UNIVERSITY PRESS
STANFORD, CALIFORNIA

Introduction to Systems Theory

Niklas Luhmann

Click to access Niklas_Luhmann_Introduction_to_System_Theory.pdf

Mysteries of cognition. Review of neocybernetics and narrative by bruce clarke.

Baecker D. (2015)

Constructivist Foundations 10(2): 261–263. http://constructivist.info/10/2/261

https://constructivist.info/10/2/261.baecker

The Communication of Meaning in Anticipatory Systems: A Simulation Study of the Dynamics of Intentionality in Social Interactions

Loet Leydesdorff

In: Daniel M. Dubois (Ed.) Proceedings of the 8th Intern. Conf. on Computing Anticipatory Systems CASYS’07, Liège, Belgium, 6-11 August 2007. Melville, NY: American Institute of Physics Conference Proceedings, Vol. 1051 (2008) pp. 33-49.

Click to access casys07.pdf

Click to access 63986_302167.pdf

Why Systems?

Dirk Baecker

Universität Witten/Herdecke http://www.uni-wh.de/baecker

Theory Culture & Society 18 (2001), pp. 59-74

Click to access 305e6a5c52e2a29190baa95c2b18c5bbe66d.pdf

LAWS OF
FORM by GEORGE SPENCER-BROWN

In collaboration with the Liverpool University
and the Laws of Form 50th Anniversary Conference.
Alphabetum III
September 28 — December 31, 2019 West Den Haag, The Netherlands

Click to access Alphabetum_III_V8_ONLINE.pdf

Systems in Context
On the outcome of the Habermas/Luhmann‐debate

Poul Kjaer

Click to access ancilla2006_66_kjaer.pdf

Niklas Luhmann and Organization Studies

Edited by
David Seidl and Kai Helge Becker

Click to access 9788763003049.pdf

A Note on Max Weber’s Unfinished Theory of Economy and Society

Dirk Baecker
Witten/Herdecke University, Germany dbaecker@uni-wh.de

Click to access vol08-no02-a6.pdf

The fractal geometry of Luhmann’s sociological theory or debugging systems theory

José Javier Blanco Rivero

CONICET/Centro de Historia Intelectual, National University of Quilmes, Roque Sáenz Peña 352, Bernal, Argentina

Technological Forecasting & Social Change 146 (2019) 31–40

Click to access blanco-rivero.pdf


Diamond Calculus of Formation of Forms

A calculus of dynamic complexions of distinctions as an interplay of worlds and distinctions

Archive-Number / Categories 3_01 / K06, K03
Publication Date 2011

Rudolf Kaehr (1942-2016)

Click to access rk_Diamond-Calculus-of-Formation-of-Forms_2011.pdf

ART AS A SOCIAL SYSTEM

Niklas Luhmann

TRANSLATED BY EVA M. KNODT

Click to access Luhmann_Niklas_Art_as_a_Social_System.pdf

Snakes all the Way Down: Varela’s Calculus for Self-Reference and the Praxis of Paradise

André Reichel*

European Center for Sustainability Research, Zeppelin University, Friedrichshafen, Germany

Systems Research and Behavioral Science Syst. Res. (2011)
Published online in Wiley Online Library (wileyonlinelibrary.com) DOI: 10.1002/sres.1105

Click to access REI_2011_Snakes.pdf

Who Conceives of Society?

Ernst von Glasersfeld

University of Massachusetts evonglas@hughes.net

Constructivist Foundations 2008, vol. 3, no. 2 http://www.univie.ac.at/constructivism/journal/

Click to access glasersfeld.pdf

Dramaturgy (sociology)

https://en.wikipedia.org/wiki/Dramaturgy_(sociology)

Dramaturgy

https://en.wikipedia.org/wiki/Dramaturgy

Beyond Bourdieu:
The Interactionist Foundations of Media Practice Theory

PETER LUNT University of Leicester, UK

International Journal of Communication 14(2020), 2946–2963

https://ijoc.org/index.php/ijoc/article/viewFile/11204/3104

Drama as Life: The Significance of Goffman’s Changing Use of the Theatrical Metaphor

Phil Manning

Sociological Theory Vol. 9, No. 1 (Spring, 1991), pp. 70-86 (17 pages) 

Published By: American Sociological Association 

https://doi.org/10.2307/201874https://www.jstor.org/stable/201874

RECONSTRUCTING THE SELF: A GOFFMANIAN PERSPECTIVE

Simon Susen

In: H. F. Dahms & E. R. Lybeck (Eds.), Reconstructing Social Theory, History and Practice. Current Perspectives in Social Theory. (pp. 111-143). Bingley, UK: Emerald. ISBN 9781786354709

https://pdfs.semanticscholar.org/b8ca/9e1bb2a4bdf97330c932fc75ea7f60253551.pdf?_ga=2.252111627.386639570.1616097397-89425557.1612485585

Mainstreaming Relational Sociology – Relational Analysis of Culture in Digithum

P. Baert. Published 2016

The Foundations of the Social: Between Critical Theory and Reflexive Sociology

S. Susen. Published 2007

Language, self, and social order: A reformulation of Goffman and Sacks

A. RawlsPublished 1989SociologyHuman Studies

The Interaction Order: American Sociological Association, 1982 Presidential Address

Author(s): Erving Goffman

Reviewed work(s):
Source: American Sociological Review, Vol. 48, No. 1 (Feb., 1983), pp. 1-17 Published by: American Sociological Association
Stable URL: http://www.jstor.org/stable/2095141 .

https://pdfs.semanticscholar.org/cc41/6add65c01434e70c1eff295ccf2c4d45ad49.pdf?_ga=2.51373867.386639570.1616097397-89425557.1612485585

Face and interaction

Michael Haugh

(2009): In Francesca Bargiela-Chiappini and Michael Haugh (eds.), Face, Communication and Social Interaction, Equinox, London, pp.1-30.

https://www.researchgate.net/publication/313098378_Face_and_Interaction

Public and private faces in web spaces – How Goffman’s work can be used to think about purchasing medicine online. 

Lisa Sugiura

Click to access LSPublic%20and%20private%20faces%20in%20web%20spaces.pdf

Organizational Analysis: Goffman and Dramaturgy  

Peter K. Manning

The Oxford Handbook of Sociology, Social Theory, and Organization Studies: Contemporary Currents

Edited by Paul Adler, Paul du Gay, Glenn Morgan, and Mike Reed

Print Publication Date: Oct 2014

https://www.oxfordhandbooks.com/view/10.1093/oxfordhb/9780199671083.001.0001/oxfordhb-9780199671083-e-012

Complete bibliography: Erving Goffman ́s writings

Persson, Anders

http://lup.lub.lu.se/search/ws/files/5499425/2438065

Chapter 1 THE PROGRAM OF INTERACTION RITUAL THEORY

Click to access s7769.pdf

A review of Jerome Bruner’s educational theory:

Its implications for studies in teaching and learning and active learning (secondary publication)

Koji MATSUMOTO

Faculty of Economics Nagoya Gakuin University

Click to access syakai_vol5401_11.pdf

The Use of Stories in Moral Development: New Psychological Reasons for an Old Education Method

DOI: 10.1037/0003-066X.45.6.709

Click to access The-Use-of-Stories-in-Moral-Development-New-Psychological-Reasons-for-an-Old-Education-Method.pdf

Narrative Understanding and Understanding Narrative

Sarah E. Worth

Contemporary Aesthetics (Journal Archive): Vol. 2 , Article 9.
Available at: https://digitalcommons.risd.edu/liberalarts_contempaesthetics/vol2/iss1/9

https://digitalcommons.risd.edu/cgi/viewcontent.cgi?article=1020&context=liberalarts_contempaesthetics

Recursion, Incursion, and Hyper-incursion

Recursion, Incursion, and Hyper-incursion

 

How do Past and Future inform the present?

What happens in the Present is not only determined by the Past but also by the Future.  Karma and Destiny both play a role as to what is going on in your life Now.

Key Terms

  • Recursion
  • Incursion
  • Hyper Incursion
  • Discrete Processes
  • Cellular Automata
  • Fractal Machine
  • Hypersets
  • Interpenetration
  • Turing Machine
  • Symmetry
  • Non Well Founded Set Theory
  • Sets as Graphs
  • Leela
  • Predetermined Future
  • Bhagya
  • Fate
  • Destiny
  • Karma
  • Anticipation
  • Four Causes of Aristotle
  • Material Cause
  • Formal Cause
  • Efficient Cause
  • Final Cause
  • Left Computer
  • Right Computer
  • Parallel Computing
  • Fifth and the Fourth in Music Theory
  • Bicameral Brain
  • Hemispheric Division of Brain
  • One, Two, Three.  Where is the Fourth?

From GENERATION OF FRACTALS FROM INCURSIVE AUTOMATA, DIGITAL DIFFUSION AND WAVE EQUATION SYSTEMS

The recursion consists of the computation of the future value of the variable vector X(t+l) at time t+l from the values of these variables at present and/or past times, t, t-l, t-2 ….by a recursive function :

X (t+ 1) =f(X(t), X(t-1) …p..)

where p is a command parameter vector. So, the past always determines the future, the present being the separation line between the past and the future.

Starting from cellular automata, the concept of Fractal Machines was proposed in which composition rules were propagated along paths in the machine frame. The computation is based on what I called “INclusive reCURSION”, i.e. INCURSION (Dubois, 1992a- b). An incursive relation is defined by:

X(t+l) =f(…, X (t+l), X(t), X(t-1) ..p..).

which consists in the computation of the values of the vector X(t+l) at time t+l from the values X(t-i) at time t-i, i=1, 2 …. , the value X(t) at time t and the value X(t+j) at time t+j, j=l, 2, …. in function of a command vector p. This incursive relation is not trivial because future values of the variable vector at time steps t+l, t+2 …. must be known to compute them at the time step t+ 1.

In a similar way to that in which we define hyper recursion when each recursive step generates multiple solutions, I define HYPERINCURSION. Recursive computational transformations of such incursive relations are given in Dubois and Resconi (1992, 1993a-b).

I have decided to do this for three reasons. First, in relativity theory space and time are considered as a four-vector where time plays a role similar to space. If time t is replaced by space s in the above definition of incursion, we obtain

X(s+ l) =f( …, X(s+ 1), X(s), X (s-l) …p.).

and nobody is astonished: a Laplacean operator looks like this. Second, in control theory, the engineers control engineering systems by defining goals in the future to compute their present state, similarly to our haman anticipative behaviour (Dubois, 1996a-b). Third, I wanted to try to do a generalisation of the recursive and sequential Turing Machine in looking at space-time cellular automata where the order in which the computations are made is taken into account with an inclusive recursion.

We have already proposed some methods to realise the design of any discrete systems with an extension of the recursion by the concept of incursion and hyperincursion based on the Fractal Machine, a new type of Cellular Automata, where time plays a central role. In this framework, the design of the model of any discrete system is based on incursion relations where past, present and future states variables are mixed in such a way that they define an indivisible wholeness invariant. Most incursive relations can be transformed in different sets of recursive algorithms for computation. In the same way, the hyperincursion is an extension of the hyper recursion in which several different solutions can be generated at each time step. By the hyperincursion, the Fractal Machine could compute beyond the theoretical limits of the Turing Machine (Dubois and Resconi, 1993a-b). Holistic properties of the hyperincursion are related to the Golden Ratio with the Fibonacci Series and the Fractal Golden Matrix (Dubois and Resconi, 1992). An incursive method was developed for the inverse problem, the Newton- Raphson method and an application in robotics (Dubois and Resconi, 1995). Control by incursion was applied to feedback systems (Dubois and Resconi, 1994). Chaotic recursions can be synchronised by incursion (1993b). An incursive control of linear, non- linear and chaotic systems was proposed (Dubois, 1995a, Dubois and Resconi, 1994, 1995). The hyperincursive discrete Lotka-Voiterra equations have orbital stability and show the emergence of chaos (Dubois, 1992). By linearisation of this non-linear system, hyperincursive discrete harmonic oscillator equations give stable oscillations and discrete solutions (Dubois, 1995). A general theory of stability by incursion of discrete equations systems was developed with applications to the control of the numerical instabilities of the difference equations of the Lotka-Volterra differential equations as well as the control of the fractal chaos in the Pearl-Verhulst equation (Dubois and Resconi, 1995). The incursion harmonic oscillator shows eigenvalues and wave packet like in quantum mechanics. Backward and forward velocities are defined in this incursion harmonic oscillator. A connection is made between incursion and relativity as well as the electromagnetic field. The foundation of a hyperincursive discrete mechanics was proposed in relation to the quantum mechanics (Dubois and Resconi, 1993b, 1995).

This paper will present new developments and will show that the incursion and hyper-incursion could be a new tool of research and development for describing systems where the present state of such systems is also a function of their future states. The anticipatory property of incursion is an incremental final cause which could be related to the Aristotelian Final Cause.

Aristotle identified four explicit categories of causation: 1. Material cause; 2. Formal cause; 3. Efficient cause; 4. Final cause. Classically, it is considered that modem physics and mechanics only deal with efficient cause and biology with material cause. Robert Rosen (1986) gives another interpretation and asks why a certain Newtonian mechanical system is in the state (phase) Ix(t) (position), v(t) (velocity)]:

1. Aristotle’s “material cause” corresponds to the initial conditions of the system [x(0), v(0)] at time t=0.

2. The current cause at the present time is the set of constraints which convey to the system an “identity”, allowing it to go by recursion from the given initial phase to the latter phase, which corresponds to what Aristotle called formal cause.

3. What we call inputs or boundary conditions are the impressed forces by the environment, called efficient cause by Aristotle.

As pointed out by Robert Rosen, the first three of Aristotle’s causal categories are tacit in the Newtonian formalism: “the introduction of a notion of final cause into the Newtonian picture would amount to allowing a future state or future environment to affect change of state in the present, and this would be incompatible with the whole Newtonian picture. This is one of the main reasons that the concept of Aristotelian finality is considered incompatible with modern science.

In modern physics, Aristotelian ideas of causality are confused with determinism, which is quite different…. That is, determinism is merely a mathematical statement of functional dependence or linkage. As Russell points out, such mathematical relations, in themselves, carry no hint as to which of their variables are dependent and which are independent.”

The final cause could impress the present state of evolving systems, which seems a key phenomenon in biological systems so that the classical mathematical models are unable to explain many of these biological systems. An interesting analysis of the Final Causation was made by Emst von Glasersfeld (1990). The self-referential fractal machine shows that the hyperincursive field dealing with the final cause could be also very important in physical and computational systems. The concepts of incursion and hyper-incursion deal with an extension of the recursive processes for which future states can determine present states of evolving systems. Incursion is defined as invariant functional relations from which several recursive models with interacting variables can be constructed in terms of diverse physical structures (Dubois & Resconi, 1992, 1993b). Anticipation, viewed as an Aristotelian final cause, is of great importance to explain the dynamics of systems and the semantic information (Dubois, 1996a-b). Information is related to the meaning of data. It is important to note that what is usually called Information Theory is only a communication theory dealing with the communication of coded data in channels between a sender and a receptor without any reference to the semantic aspect of the messages. The meaning of the message can only be understood by the receiver if he has the same cultural reference as the sender of the message and even in this case, nobody can be sure that the receiver understands the message exactly as the sender. Because the message is only a sequential explanation of a non-communicable meaning of an idea in the mind of the sender which can be communicated to the receiver so that a certain meaning emerges in his mind. The meaning is relative or subjective in the sense that it depends on the experiential life or imagination of each of us. It is well- known that the semantic information of signs (like the coding of the signals for traffic) are the same for everybody (like having to stop at the red light at a cross roads) due to a collective agreement of their meaning in relation to actions. But the semantic information of an idea, for example, is more difficult to codify. This is perhaps the origin of creativity for which a meaning of something new emerges from a trial to find a meaning for something which has no a priori meaning or a void meaning.

Mind dynamics seems to be a parallel process and the way we express ideas by language is sequential. Is the sequential information the same as the parallel information? Let us explain this by considering the atoms or molecules in a liquid. We can calculate the average velocity of the particles from in two ways. The first way is to consider one particular particle and to measure its velocity during a certain time. One obtains its mean velocity which corresponds to the mean velocity of any particle of the liquid. The sec- ond way is to consider a certain number of particles at a given time and to measure the velocity of each of them. This mean velocity is equal to the first mean velocity. So there are two ways to obtain the same information. One by looking at one particular element along the time dimension and the other by looking at many elements at the same time. For me, explanation corresponds to the sequential measure and understanding to the parallel measure. Notice that ergodicity is only available with simple physical systems, so in general we can say that there are distortions between the sequential and the parallel view of any phenomenon. Perhaps the brain processes are based on ergodicity: the left hemisphere works in a sequential mode while the right hemisphere works in a parallel mode. The left brain explains while the right brain understands. The two brains arecomplementary and necessary.

Today computer science deals with the “left computer”. Fortunately, the informaticians have invented parallel computers which are based on complex multiplication of Turing Machines. It is now the time to reconsider the problem of looking at the “right computer”. Perhaps it will be an extension of the Fractal Machine (Dubois & Resconi, 1993a).

I think that the sequential way deals with the causality principle while the parallel way deals with a finality principle. There is a paradox: causality is related to the successive events in time while finality is related to a collection of events at a simultaneous time, i.e. out of time.Causality is related to recursive computations which give rise to the local generation of patterns in a synchronic way. Finality is related to incursive or hyperincursive symmetry invariance which gives rise to an indivisible wholeness, a holistic property in a diachronic way. Recursion (and Hyper recursion) is defined in the Sets Theory and Incursion (and Hyperincursion) could be defined in the new framework of the Hypersets Theory (Aczel, 1987; Barwise, Moss, 1991).

If the causality principle is rather well acknowledged, a finality principle is still controversial. It would be interesting to re-define these principles. Causality is defined for sequential events. If x(t) represents a variable at time t, a causal rule x(t+l) = f(x(t)) gives the successive states of the variable x at the successive time steps t, t+l, t+2, … from the recursive functionf(x(t)), starting with an initial state x(0) at time t=0. Defined like this, the system has no degrees of freedom: it is completely determined by the function and the initial condition. No new things can happen for such a system: the whole future is completely determined by its past. It is not an evolutionary system but a developmental system. If the system tends to a stable point, x(t+l) = x(t) and it remains in this state for ever. The variable x can represent a vector of states as a generalisation.

In the same way, I think that determinism is confused with predictability, in modern physics. The recent fractal and deterministic chaos theory (Mandeibrot, 1982; Peitgen, Jurgens, Saupe, 1992) is a step beyond classical concepts in physics. If the function is non-linear, chaotic behaviour can appear, what is called (deterministic) chaos. In this case, determinism does not give an accurate prediction of the future of the system from its initial conditions, what is called sensitivity to initial conditions. A chaotic system loses the memory of its past by finite computation. But it is important to point out that an average value, or bounds within which the variable can take its values, can be known;

it is only the precise values at the successive steps which are not predictable. The local information is unpredictable while the global symmetry is predictable. Chaos can presents a fractai geometry which shows a self-similarity of patterns at any scale.

A well-known fractal is the Sierpinski napkin. The self-similarity of pattems at any scale can be viewed as a symmetry invariance at any scale. An interesting property of such fractals is the fact that the final global pattern symmetry can be completely independent of the local pattern symmetry given as the initial condition of the process from which the fractal is built. The symmetry of the fractal structure, a final cause, can be independent of the initial conditions, a material cause. The formal cause is the local symmetry of the generator of the fractal, independently of its material elements and the efficient cause can be related to the recursive process to generate the fractal. In this particular fractal geometry, the final cause is identical to the final cause. The efficient cause is the making of the fractal and the material cause is just a substrate from which the fractal emerges but this substrate doesn’t play a role in the making.

Finally, the concepts of incursion and hyperincursion can be related to the theory of hypersets which are defined as sets containing themselves. This theory of hypersets is an alternative theory to the classical set theory which presents some problems as the in- completeness of G6del: a formal system cannot explain all about itself and some propositions cannot be demonstrated as true or false (undecidability). Fundamental entities of systems which are considered as ontological could be explain in a non-ontological way by self-referential systems.

Please see my related posts

On Anticipation: Going Beyond Forecasts and Scenarios

Autocatalysis, Autopoiesis and Relational Biology

Key sources of Research

 

Computing Anticipatory Systems with Incursion and Hyperincursion

Daniel M. DUBOIS

 

Click to access cd554835f0ae367c3d3e3fa40f3e5e5f5f11.pdf

 

 

 

Anticipation in Social Systems:

the Incursion and Communication of Meaning

Loet Leydesdorff 

Daniel M. Dubois

Click to access casys03.pdf

 

 

 

GENERATION OF FRACTALS FROM INCURSIVE AUTOMATA, DIGITAL DIFFUSION AND WAVE EQUATION SYSTEMS

Daniel M. Dubois

 

Click to access dubois.pdf

 

 

 

Non-wellfounded Set Theory

https://plato.stanford.edu/entries/nonwellfounded-set-theory/

Hypersets

  • Jon Barwise &
  • Larry Moss

The Mathematical Intelligencer

volume 13, pages31–41(1991)

https://link.springer.com/article/10.1007/BF03028340

Non-well-founded set theory

https://en.wikipedia.org/wiki/Non-well-founded_set_theory

Shapes and Patterns in Nature

Shapes and Patterns in Nature

 

There are so many colors, shapes, and patterns in nature.

  • Seashells
  • Animal Skins (Zebra, Leopard)
  • Butterflies
  • Shape of Plants
  • Flowers (Sun Flower)
  • Fruits (Pineapple)

How do we explain these from perspective of science?  There are several branches of science which have explored these questions for decades.  There are Reaction Diffusion Models and Cellular Automata models explaining development of patterns on seashells, plants and animal skins.  There is L-system developed by Aristid Lindenmayer to explain development of plants.  It is a fascinating subject.

 

From Exploring Complex Forms in Nature Through Mathematical Modeling: A Case on Turritella Terebra

There are several studies have been carried out in a number of scientific disciplines, such as mathematics, biology, paleontology and computer engineering to understand and decipher the relations of the seashells complex forms. Starting with Descartes, Figure 4 shows a time line in which many investigators having focused on the curves of these shells and their mathematical properties. They all outlined a number of mathematical relations that control the overall geometry of seashells.

After examining the existing seashell models in literature it is seen that they all followed Raup’s model which roughly abstracts the seashell form using three parameters; whorl (rate of expansion of the generating curve), distance (relative distance between the generating curve and axis of coiling), and translation (the change of the cone’s movement along an axis with respect to the whorl), an ellipse as the whorl cross-section as well. However, it is clear from the observations of actual shells (Figure 5) that the cross-section is more complex than the input that the three parameters allow. In the pursuit of realistic visualizations, Kawaguchi enhanced the appearance of shell models using filled polygons which represented the surface of shells more convincingly than line drawings. Similar techniques were used subsequently by Oppenheimer (1986). A different approach was adopted by Pickover (1989) who approximated shell surfaces by using interpenetrating spheres. Illert (1989) introduced Frenet Frames (Bronsvoort, 1985) to precisely orient the opening of a shell. His model also captured a form of surface sculpture. Cortie (1989) studied the pattern forms on the surface of the shell model (Meinhardt, 2003). Finally, the model of seashell geometry by Fowler et al. (2003) was similar to that introduced by Raup, and was the first to implement free-form cross sections using a Bézier curve (Farin, 2002 Rogers, 2001) as the input. It can be claimed that, studies above all focused on modeling the appearance of the shell surface.

All these approaches can be considered as a milestone for their era, as each model reflects the observation and tools of measurement, modeling and technologies of their time. In all these approaches seashells were modeled as a single surface, as a twodimensional object, and embedded in three-dimensional space. Today, such modeling research should be carried out employing observation tools, knowledge, information, and computational technologies to the maximum extent. For this reason, we developed a mathematical model that can be transformed into a computational model for further studies (such as overall behavior of shells, form-structure relations, form finding explorations etc.) to explore potentials of such optimized forms.

 

From Exploring Complex Forms in Nature Through Mathematical Modeling: A Case on Turritella Terebra

 

patterns

 

From Computational models of plant development and form

A broad program of using mathematical reasoning in the study of the development and form of living organisms was initiated almost 100 yr ago by D’Arcy Thompson (1942) in his landmark book On Growth and Form (see Keller, 2002, for a historical analysis). One of his most influential contributions was the ‘theory of transformations’, which showed how forms of different species could be geometrically related to each other. The theory of transformations was extended to relate younger and older forms of a developing organism (Richards & Kavanagh, 1945), but did not incorporate the formation and differentiation of new organs. This limitation was addressed a quarter of a century later by Lindenmayer (1968, 1971), who introduced an original mathematical formalism, subsequently called L-systems, to describe the development of linear and branching structures at the cellular level. By the mid 1970s, computational models based on Lsystems and other formalisms had been applied to study several aspects of plant development, including the development of leaves and inflorescences, and the formation of phyllotactic patterns (Lindenmayer, 1978). The questions being asked included the impact of distinct modes of information transfer (lineage vs interaction) on plant development, and the relationship between local development and global form. Similar interests underlied the independent pioneering work of Honda and co-workers on the modeling of trees (Honda, 1971; Borchert & Honda, 1984).

Another class of models was pioneered by Turing (1952), who showed mathematically that, in a system of two or more diffusing reagents, a pattern of high and low concentrations may spontaneously emerge from an initially uniform distribution. This was a surprising result, as it appeared to contradict the second law of thermodynamics: the general tendency of systems to proceed from more organized states toward disorder (the apparent paradox is resolved by jointly considering the reaction–diffusion system and its surroundings). Related models were introduced, under the name of activator–inhibitor and activator-substrate (depletion) systems, by Gierer & Meinhardt (1972), and extensively investigated by Meinhardt (1982). Reaction–diffusion systems showed how, in principle, molecular-level interactions may lead to morphogenesis and differentiation. In plants, reaction– diffusion-type models have been used to explain the patterning of trichomes in leaves and hair cells in roots (Digiuni et al., 2008; Savage et al., 2008; Jo¨nsson & Krupinski, 2010; Benı´tez et al., 2011). Nevertheless, the extent to which reaction–diffusion models apply to the plant kingdom appears to be limited (Kepinski & Leyser, 2005; Berleth et al., 2007). A significant role is played instead by mechanisms involving active transport of the plant hormone auxin (Section V). In some cases, such as the generation of phyllotactic patterns, this reliance on active transport is difficult to explain in evolutionary terms, as reaction–diffusion systems can generate the same patterns. Spatio-temporal coordination of other developmental processes, however, such as bud activation, requires long-distance signaling. Active transport may thus have evolved to overcome the limitations of diffusion, which is very slow over long distances (Crick, 1971).

In the last decade, computational modeling has become a mainstream technique in developmental plant biology, as reflected in numerous reviews (e.g. Prusinkiewicz, 2004b; Prusinkiewicz & Rolland-Lagan, 2006; Grieneisen & Scheres, 2009; Chickarmane et al., 2010; Jo¨nsson&Krupinski, 2010; Jo¨nsson et al., 2012). On the one hand, the sequencing of the human genome put in focus the chasm between knowing the genome of an organism and understanding how this organismdevelops and functions.Computational models bridge this chasm. On the other hand, successes of early conceptual models that relate patterns of gene expression to the form of animals (Lawrence, 1992) and plants (Coen & Meyerowitz, 1991) have prompted a quest for a comprehensive, mechanistic understanding of development (Coen, 1999). Current experimental techniques for tracking growth and observing marked proteins in living tissues (Reddy et al., 2004; Fernandez et al., 2010) are yielding a wealth of data that correlate molecular-level processes with plant development and form. Computational models play an increasingly important role in interpreting these data.

The use of models has been accelerated by the advancements in computer hardware, software, and modeling methodologies. General-purpose mathematical software (e.g. Mathematica and MATLAB), modeling programs built on the basis of this software (e.g. GFtbox, Kennaway et al., 2011) and specialized packages for modeling plants (e.g. the Virtual Laboratory and L-studio (Prusinkiewicz, 2004a), OpenAlea (Pradal et al., 2008) and VirtualLeaf (Merks et al., 2011)) facilitate model construction, compared with general-purpose programming languages. Furthermore, current computers are sufficiently fast to simulate and visualize many models at interactive or close-to-interactive rates, which is convenient for model exploration.

 

From The reaction-diffusion system: a mechanism for autonomous pattern formation in the animal skin

In his paper entitled ‘The chemical basis of morphogenesis’ Turing presented a ground-breaking idea that a combination of reaction and diffusion can generate spatial patterns (Turing 1952). In the paper, he studied the behaviour of a complex system in which two substances interact with each other and diffuse at different diffusion rates, which is known as the reaction–diffusion (RD) system. Turing proved mathematically that such system is able to form some characteristic spatio-temporal patterns in the field. One of the most significant deviations is s formation of a stable periodic pattern. He stated that the spatial pattern generated by the system might provide positional information for a developing embryo.

In spite of the importance of the idea in the developmental biology, his model was not accepted by most experimental biologists mainly because there were no experimental technologies available to test it. Therefore, most of those who took over and developed the Turing’s idea were applied mathematicians and physicists. They proposed various types of model that developed Turing’s original equation to fit real, naturally occurring phenomena (Meinhardt 1982; Murray & Myerscough 1991; Murray 1993; Nagorcka & Mooney 1992). Although the equations for each model differ, they all share the basic requirement of the original model; that is, ‘waves’ are made from the interactions of two putative chemical substances which we refer to here as the ‘activator’ and the ‘inhibitor’ (Meinhardt 1982).

 

Key Terms

  • Development Biology
  • Mathematical Biology
  • Biomathematics
  • Morphogenesis
  • Phyllotaxis
  • Evolutionary Biology
  • Nonlinear dynamical systems
  • Cellular Automata
  • Fractals
  • Iterated Systems
  • L-Systems
  • Pattern Formation
  • IFS (Iterated Functions Set)
  • Theoretical Biology
  • diffusion–reaction (DR) model
  • Systems Biology
  • Code Biology
  • Computational Biology
  • Algorithmic Biology
  • Complex Systems
  • Turing Patterns

 

 

Key People:

  • D’Arcy Wentworth Thompson
  • Aristid Lindenmayer
  • Alan Turing
  • Hans Meinhardt
  • Philip Ball
  • Przemyslaw Prusinkiewicz
  • Murray JD
  • Stephen Wolfram

 

 

Key Sources of Research:

 

On Growth and Form

Thompson D’Arcy W.

(1952)

 

 

The Algorithmic Beauty of Plants

Prusinkiewicz, Przemyslaw, Lindenmayer, Aristid

 

 

The Algorithmic Beauty of Seashells

Meinhardt H, Prusinkiewicz P, Fowler D

(2003)

(Springer, New York), 3rd Ed.

 

 

The Algorithmic Beauty of Seaweeds, Sponges and Corals

Kaandorp, Jaap A., Kübler, Janet E.

 

 

Mathematical Biology

Murray JD

(2003)

 

 

Models of biological pattern formation

Meinhardt H

(1982)

 

 

The chemical basis of morphogenesis.

Turing A

(1952)

Click to access Turing.pdf

 

 

Pattern formation by coupled oscillations: The pigmentation patterns on the shells of molluscs

Hans Meinhardt, Martin Klingler

 

 

The Self-Made Tapestry Pattern formation in nature

Philip Ball

1999

 

 

Models of biological pattern formation in space and time

Hans Meinhardt

2014

Click to access Meinhardt.pdf

 

 

Models of biological pattern formation

Hans Meinhardt,

Click to access Hans_Meinhardt.pdf

 

 

 

Cellular Automata, PDEs, and Pattern Formation

 

Click to access 1003.1983.pdf

 

 

The Computational Beauty of Nature: Computer Explorations of Fractals, Chaos, Complex Systems, and Adaptation

By Gary William Flake

 

 

The Curves of Life

Cook, T

1979

Dover Publications, Inc. New York.

 

 

Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation

Shigeru Kondo1* and Takashi Miura

2010

Click to access reaction-diffusion_model_as_a_framework_for_understanding_biological_pattern_formation.pdf

Click to access kondomiura10science.pdf

 

 

The Hegemony of Molecular Biology

PHILIP KITCHER

 

Click to access kitcher99-hegemony.pdf

 

 

Modeling seashells

 

Deborah R. Fowlery􏰣, Hans Meinhardtz and Przemyslaw Prusinkiewicz

Click to access shells.sig92.pdf

 

 

The neural origins of shell structure and pattern in aquatic mollusks

Alistair Boettigera, Bard Ermentroutb, and George Oster

2009

Click to access 6837.full.pdf

 

 

Mechanical basis of morphogenesis and convergent evolution of spiny seashells

Régis Chirata, Derek E. Moultonb,1, and Alain Goriely

2013

 

Click to access 6015.full.pdf

 

 

The Geometry and Pigmentation of Seashells

S Coombes

2009

Click to access Seashells09.pdf

 

 

PATTERNS IN NATURE

Richie Khandelwal

Sahil Sahni

 

Click to access P7.pdf

 

 

Forging patterns and making waves from biology to geology: a commentary on Turing (1952) ‘The chemical basis of morphogenesis’

Philip Ball

 

Click to access f989a13264a455ec2898ed361b1c435b5f0c.pdf

 

 

Mollusc Shell Pigmentation: Cellular Automaton Simulations and Evidence for Undecidability

INGO KUSCH AND MARIO MARKUS

1995

 

Click to access KuschMarkus1996.pdf

 

 

Pattern Formation in Reaction-Diffusion Systems

Masayasu Mimura

 

Click to access 7adbe7e696d4ba9ad3a89fed4ba15549a091.pdf

 

 

The Natural 3D Spiral

Gur Harary and Ayellet Tal

 

Click to access 11-HararyTal.pdf

 

 

A Model for Pattern Formation on the Shells of Molluscs

HANS MEINHARDT AND MARTIN KLINGLER

1987

Click to access Meinhardt_1987.pdf

 

 

 

The reaction-diffusion system: a mechanism for autonomous pattern formation in the animal skin

 

Shigeru Kondo

Click to access The%20reaction-diffusion%20system_%20a%20mechanism%20for%20autonomous.pdf

 

 

Mechanical growth and morphogenesis of seashells

Derek E. Moulton, Alain Goriely and R ́egis Chirat

 

Click to access finalOR01.pdf

 

 

Scaling of morphogenetic patterns in continuous and discrete models

 

Click to access RasolonjanaharyMan_Sep2013_17293.pdf

 

 

On the Dynamics of a Forced Reaction-Diffusion Model for Biological Pattern Formation

A A Tsonis, JB Elsner, P A Tsonis

Click to access TsonisElsnerTsonis1989.pdf

 

 

 

A Model for Pattern Formation on the Shells of Molluscs

H M

Click to access 5_doc.pdf

 

 

Impact of Turing’s Work

Maini

Click to access 172.pdf

 

 

The possible role of reaction–diffusion in leaf shape

Nigel R. Franks1* and Nicholas F. Britton

 

Click to access 10972123.pdf

 

 

Pattern regulation in the stripe of zebrafish suggests an underlying dynamic and autonomous mechanism

Motoomi Yamaguchi*†, Eiichi Yoshimoto‡, and Shigeru Kondo

 

Click to access yamaguchi2007.pdf

 

 

Turing Patterns

P Ball

Click to access Turing_long.pdf

 

 

 

MODELS FOR PIGMENT PATTERN FORMATION IN THE SKIN OF FISHES

K.J. PAINTER

Click to access kjp006.pdf

 

 

 

Web Resource for Algorithmic Botony 

http://algorithmicbotany.org/papers/

 

 

FRACTAL GEOMETRY AND SUPERFORMULA TO MODEL NATURAL SHAPES

Nicoletta Sala

2013

Click to access ijrras_16_4_09.pdf

 

 

The Geometry of Seashells

Dr S Coombes

 

Click to access SeaShells.pdf

 

 

SEASHELLS: THE PLAINNESS AND BEAUTY OF THEIR MATHEMATICAL DESCRIPTION

JORGE PICADO

 

Click to access article.pdf

 

 

Models for the morphogenesis of the molluscan shell

 

Click to access molluscanshell.pdf

 

 

Modeling Seashell Morphology

 

Click to access AE-MKMpre.pdf

 

 

Exploring Complex Forms in Nature Through Mathematical Modeling: A Case on Turritella Terebra

 

Click to access ecaade2009_164.content.pdf

 

 

The Neural Origins of Sea Shell Patterns

Click to access Shells.pdf

 

 

Biological Pattern Formation : from Basic Mechanisms to Complex Structures

A. J. Kochy and H. Meinhardt

 

 

Form-Optimizing in Biological Structures The Morphology of Seashells

EDGAR STACH University of Tennessee

 

 

A Theory of Biological Pattern Formation

A. Gierer and H. Meinhardt

1972

 

Click to access gierer_meinhardt.pdf

 

 

Cellular Automata as Models of Complexity

Stephen Wolfram,

Nature 311 (5985): 419–424, 1984

Click to access 006_Wolfram1984.pdf

 

 

Website on Oliva Porphyria

http://oliva.porphyria.free.fr/menu%20GB.html

 

 

Evolution of patterns on Conus shells

Zhenqiang Gonga, Nichilos J. Matzkeb, Bard Ermentroutc, Dawn Songa, Jann E. Vendettib, Montgomery Slatkinb, and George Oster

 

Click to access 2012%20Evolution%20of%20patterns%20on%20Conus%20shells%20_E234.full.pdf

 

 

Theoretical aspects of pattern formation and neuronal development

http://www.eb.tuebingen.mpg.de/de/forschung/emeriti/hans-meinhardt/home.html

 

 

20+ Photos Of Geometrical Plants For Symmetry Lovers

http://www.boredpanda.com/geometry-symmetry-plants-nature/

 

 

Computational models of plant development and form

Przemyslaw Prusinkiewicz and Adam Runions

 

Click to access tansley.np2012.pdf

 

 

Periodic pattern formation in reaction–diffusion systems: An introduction for numerical simulation

Takashi Miura* and Philip K. Maini

 

Click to access 173.pdf

 

 

Dynamics of Complex Systems

Yaneer Bar-yam

http://necsi.edu/publications/dcs/index.html#fulltext