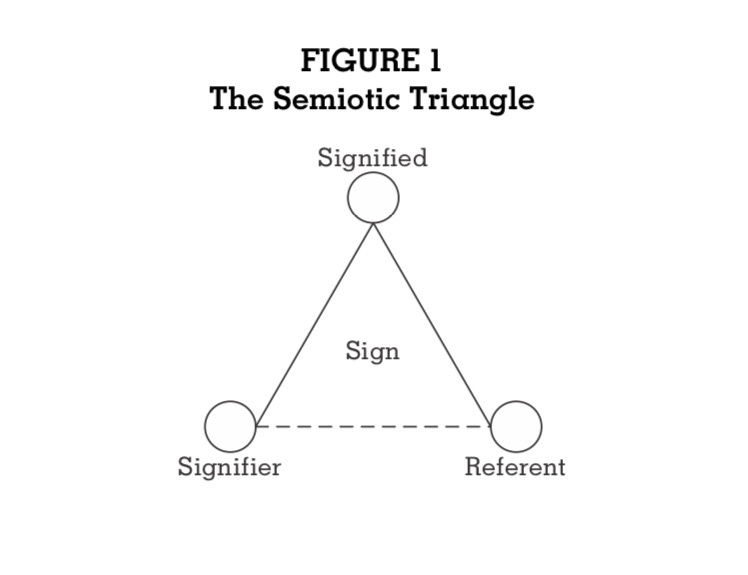
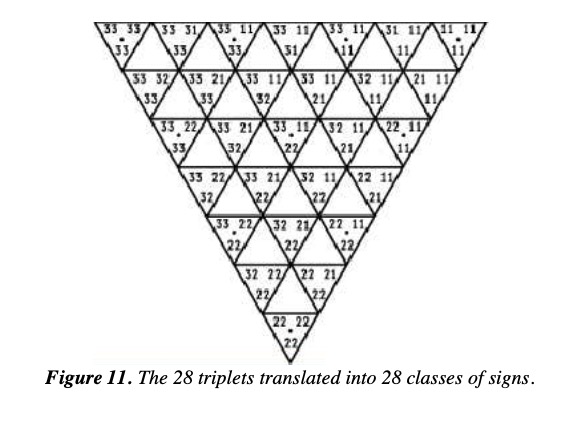
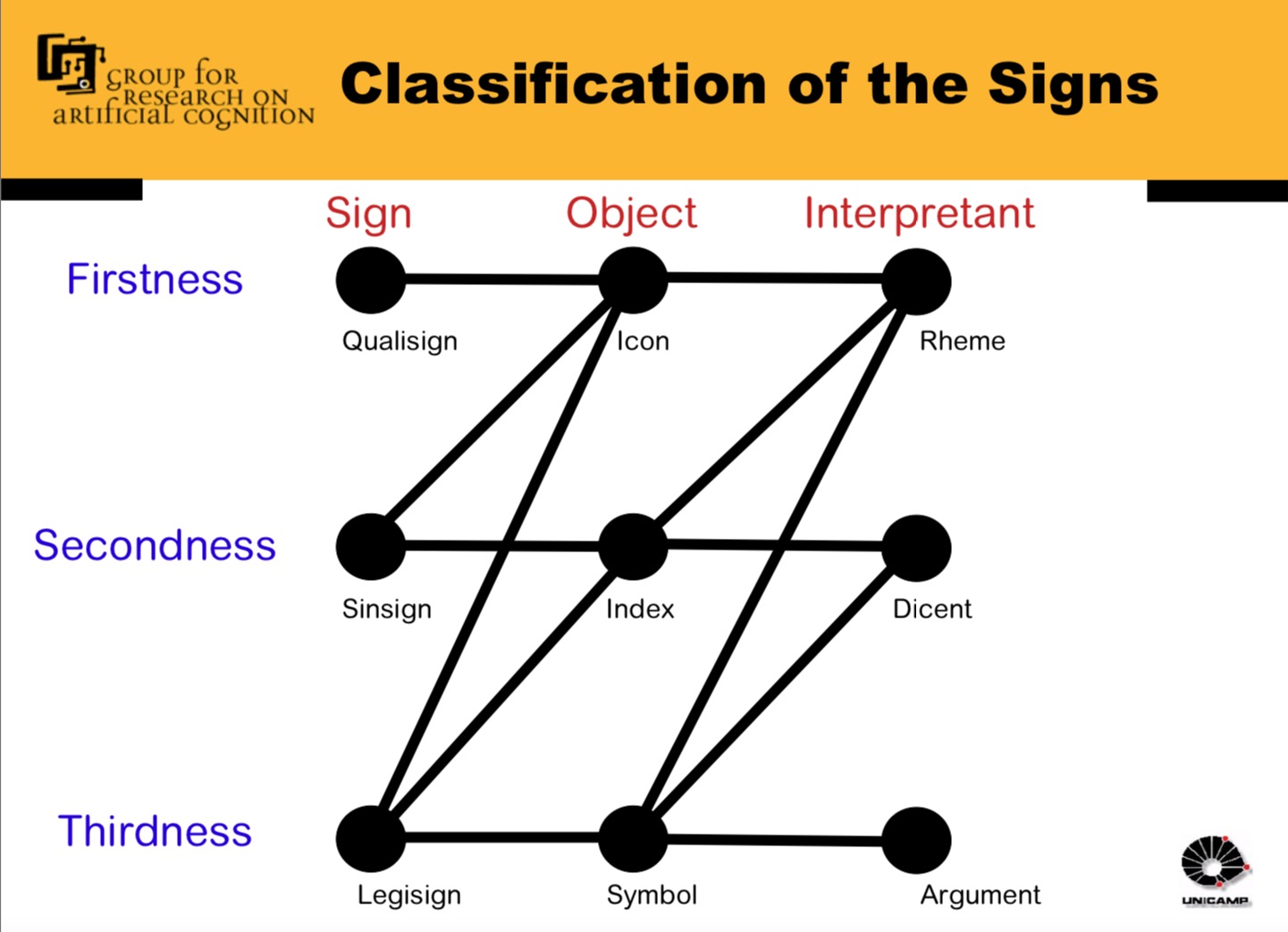
Charles Sanders Peirce’s Continuum

Key Terms
- Charles Sanders Peirce
- Continumm
- Continuity
- Continua
- Cantor’s Continua
- Triadic Logic
- Trivalent Logic
- Three Valued Logic
- Multi Valued Logic
- Modality
- Bivalent Logic
- Cosmology
- Infinite
- Infinitesimal
- Perception
- Potentiality
- Principle of Continuity
- Realism
- Synechism
- Topology
- Principle of Excluded Middle
- Nested Continua Model
Continuity, Continuum, and Continua
- What is Continuity, Continuum and Continua?
- History of Continuum and Continua
- Varieties of Continuum
- Peirce’s Continuum
- Continuum East and west
- Peirce’s Nested Continua
- Continuous and Discrete
- Parts and No Parts (Whole)
- Category Theory
- Set Theory
- Peirce’s Theory of Collections
- Peirce’s Diagrams and Existential Graphs
- Indivisibility
- Number Theory and Mathematical Continuum
- Topical/Topological Continuum
- Cantor / Dedekind Continuum
- Intuitive Continuum
- Primordial Continuum
- Large Set Theoretic Continuum
- Category Theoretic Continuum
- Sheaf Continuum
- Euclidean Geometry
- Non Euclidean Geometry
- Archimedean Geometry
- Non Archimedean Geometry
- Complex Numbers and Fractals
- Non Archimedean Systems
- Nonstandard (Robinsonian) Continuum
- Nilpotent Infinitesimalist Continuum
- Point Free Continuum
- Mereology
- Mereotopology
History of Continua
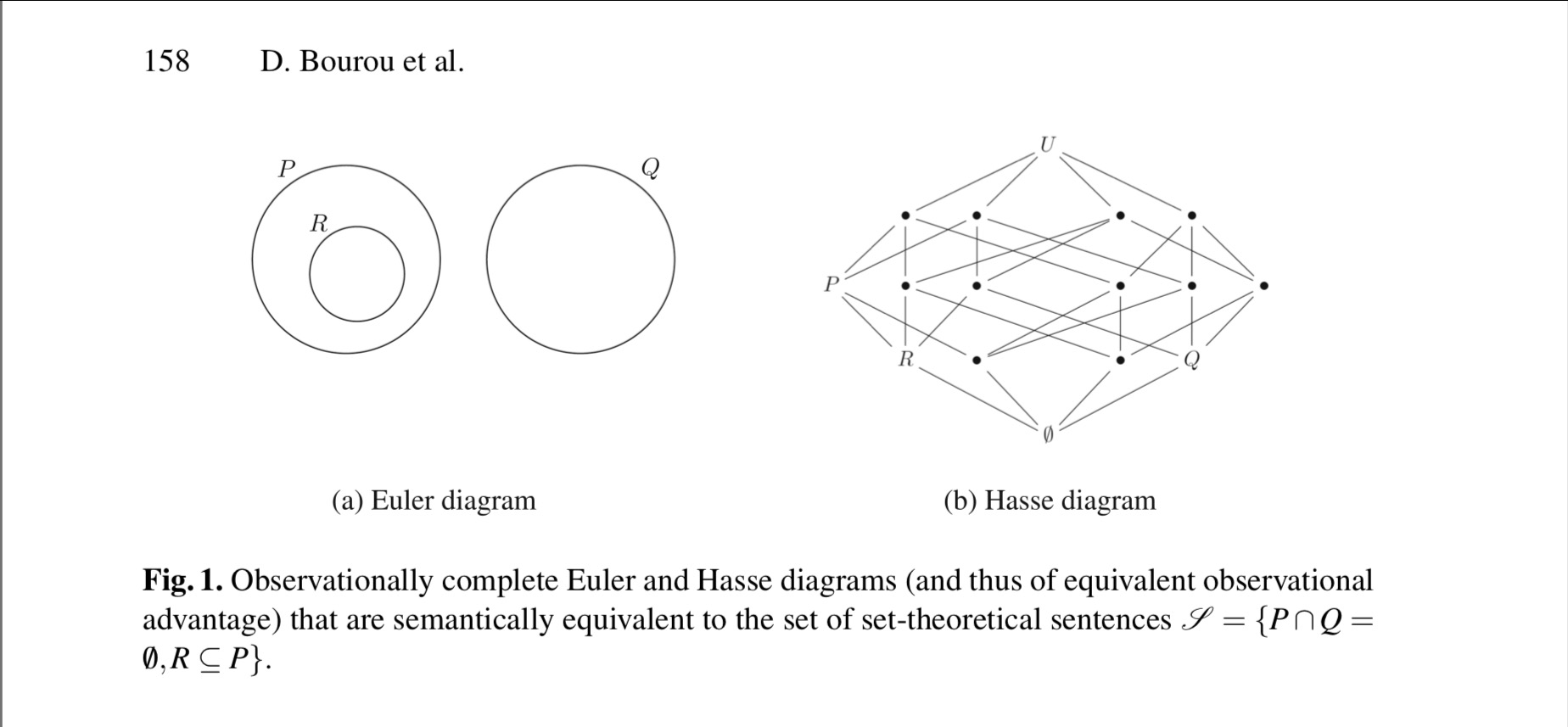
Source: The History of Continua: Philosophical and Mathematical Perspectives
Mathematical and philosophical thought about continuity has changed considerably over the ages. Aristotle insisted that continuous substances are not composed of points, and that they can only be divided into parts potentially; a continuum is a unified whole. The most dominant account today, traced to Cantor and Dedekind, is in stark contrast with this, taking a continuum to be composed of infinitely many points. The opening chapters cover the ancient and medieval worlds: the pre-Socratics, Plato, Aristotle, Alexander, and a recently discovered manuscript by Bradwardine. In the early modern period, mathematicians developed the calculus the rise of infinitesimal techniques, thus transforming the notion of continuity. The main figures treated here include Galileo, Cavalieri, Leibniz, and Kant. In the early party of the nineteenth century, Bolzano was one of the first important mathematicians and philosophers to insist that continua are composed of points, and he made a heroic attempt to come to grips with the underlying issues concerning the infinite. The two figures most responsible for the contemporary hegemony concerning continuity are Cantor and Dedekind. Each is treated, along with precursors and influences in both mathematics and philosophy. The next chapters provide analyses of figures like du Bois-Reymond, Weyl, Brouwer, Peirce, and Whitehead. The final four chapters each focus on a more or less contemporary take on continuity that is outside the Dedekind–Cantor hegemony: a predicative approach, accounts that do not take continua to be composed of points, constructive approaches, and non-Archimedean accounts that make essential use of infinitesimals.
Keywords: continuity, Aristotle, infinity, infinitesimal, Dedekind, Cantor, point, intuitionism, Archimedean, indivisibles
Key Scholars
- Plato
- Aristotle
- Parmenides
- Zeno
- Alexander of Aphrodisias
- Thomas Bradwardine
- Bernard Bolzano
- Galileo Galilei
- Bonaventura Cavalieri
- Gottfried Wilhelm Leibniz
- Cauchey
- Immanuel Kant
- Georg Cantor
- Richard Dedekind
- Paul du Bois-Reymond
- Hermann Weyl
- Giuseppi Veronese
- L. E. J. Brouwer
- Alfred NorthWhitehead
- Charles Sanders Peirce
- Abraham Robinson
20th/21st Century Scholars
- Matthew E. Moore
- John L. Bell
- Jerome Havenel
- Fernando Zalamea
- Gary Slater
- Peter Ochs
- Francesco Bellucci
- Jon Alan Schmidt
- D. A. Anapolitanos
- D. Christopoulou
- Robert Lane
- Teppei Hayashi
- Philip Ehrlich
- Geoffrey Hellman
- Stewart Shapiro
- Marc Champagne
Varieties of Continua
Source: Varieties of Continua: From Regions to Points and Back
- Ancient Atomism
- Aristotle
- Dedekind Cantor
- Non Standard Analysis
- Intuitionistic Analysis
- Smooth Infinitesimal Analysis
- Point based Predicative Analysis
- Point Free Geometry and Analysis
Source: CONTEMPORARY INFINITESIMALIST THEORIES OF CONTINUA AND THEIR LATE 19TH- AND EARLY 20TH-CENTURY FORERUNNERS
- Real Number System = Arithematic Continuum
- Geometric Linear Continuum
- Cantor Dedekind Axiom
- Constructivist & Predicativist Theories
- Infinitesimal Theories
- Alain Connes’s Noncommutative (Differential) Geometry
- Nonstandard Analysis
- Nilpotent Infinitesimalist approaches to portions of differential geometry
- Theory of Surreal Numbers
Emergence of Non Archimedean Systems of Magnitudes
- Non archimedean geometry of G. Veronese
- Tullio Levi-Civita
- David Hilbert
- Celebrated algebraico -set-theoretic work of Hans Hahn
- du Bois-Reymond on the rates of growth of real functions
- G. H. Hardy
- Felix Hausdorff
Nonstandard Theories of Continua
- Archimedean Axiom
- Veronese’s Theory of Continua
- Hahn’s non archimedean generalizations of the archimedean arithmetic continuum
- Pantachies of du Bois-Reymond and Hausdorff
- Elementary Continua
- Nonstandard (Robinsonian) Continua
- The absolute arithmetic continuum: Conway’s system of Surreal Numbers
- Hjelmslev’s Nilpotent Infinitesimalist Continuum
- Infinitesimalist Approches to differential geometry of Smooth Manifolds and their underlying continua
- Invertible and Nilpotent infinitesimals afterthoughts
Charles Sanders Peirce’s Continuum
Evolution of Peirce’s Continuum
Source: Peirce on Continuity (Chapter 8 of Book by Vincent G Potter)
- Pre Cantorian Until 1884
- Cantorian 1884 – 1894
- Kantistic 1895 – 1908
- Post Cantorian 1908 – 1911
Source: Peirce’s Clarifications of Continuity / Jerome Havenel – Five Periods
- Anti Nominalistic Period (1868 – 1884)
- Cantorian Period (1884 – 1892)
- Infinitesimal Period (1892 – 1897)
- Super Multitudinous Period (1897 – 1907)
- Topological Period (1908 – 1913)
Source: Logic of Relations and Diagrammatic Reasoning / Note 24
Scholars have explained how “continuity” is fundamental to Peirce’s mature philosophy; see Hookway (1985), Stjernfelt (2007) and Zalamea (2010). Moore (2015) evaluates Peirce’s description from a mathematical point of view. Dauben (1982) presents in some detail Peirce’s conception of the continuum from the point of view of set theory.
Source: The Continuity of Peirce’s Thought
A comprehensive and systematic reconstruction of the philosophy of Charles S. Peirce, perhaps America’s most far-ranging and original philosopher, which reveals the unity of his complex and influential body of thought.
We are still in the early stages of understanding the thought of C. S. Peirce (1839-1914). Although much good work has been done in isolated areas, relatively little considers the Peircean system as a whole. Peirce made it his life’s work to construct a scientifically sophisticated and logically rigorous philosophical system, culminating in a realist epistemology and a metaphysical theory (“synechism”) that postulates the connectedness of all things in a universal evolutionary process.
In The Continuity of Peirce’s Thought, Kelly Parker shows how the principle of continuity functions in phenomenology and semeiotics, the two most novel and important of Peirce’s philosophical sciences, which mediate between mathematics and metaphysics. Parker argues that Peirce’s concept of continuity is the central organizing theme of the entire Peircean philosophical corpus. He explains how Peirce’s unique conception of the mathematical continuum shapes the broad sweep of his thought, extending from mathematics to metaphysics and in religion. He thus provides a convenient and useful overview of Peirce’s philosophical system, situating it within the history of ideas and mapping interconnections among the diverse areas of Peirce’s work.
This challenging yet helpful book adopts an innovative approach to achieve the ambitious goal of more fully understanding the interrelationship of all the elements in the entire corpus of Peirce’s writings. Given Peirce’s importance in fields ranging from philosophy to mathematics to literary and cultural studies, this new book should appeal to all who seek a fuller, unified understanding of the career and overarching contributions of Peirce, one of the key figures in the American philosophical tradition.
Source: Peirce’s Logic of continuity: a conceptual and mathematical approach to the continuum and the existential graphs
Peirce’s logic of continuity is explored from a double perspective: (i) Peirce’s original understanding of the continuum, alternative to Cantor’s analytical Real line, (ii) Peirce’s original construction of a topological logic – the existential graphs – alternative to the algebraic presentation of propositional and first-order calculi. Peirce’s general architectonics, oriented to back-and-forth hierarchical crossings between the global and the local, is reflected with great care both in the continuum and the existential graphs.

Source: Two New Gestures on Peirce’s Continuum and the Existential Graphs: Plurality of Pragmatic Imagination

Source: Two New Gestures on Peirce’s Continuum and the Existential Graphs: Plurality of Pragmatic Imagination

Source: Two New Gestures on Peirce’s Continuum and the Existential Graphs: Plurality of Pragmatic Imagination

Source: Two New Gestures on Peirce’s Continuum and the Existential Graphs: Plurality of Pragmatic Imagination

Source: Does Continuity Allow For Emergence?
The present paper proposes an emergentist reading of Peirce, with special reference to his concept of evolution. Although the author never adopts the word “emergence” in a technical manner, it will be demonstrated that the core problem of emergence lies at the heart of his evolutionary doctrine, generally displayed by the interplay of his three well-known categories of Firstness, Secondness and Thirdness. Indeed, although the Classical pragmatists most quoted in connection to emergentism are Dewey and Mead (and William James to some degree), scholars have recently suggested some emergentist readings of Peirce’s thought (cf. above all Tiercelin 1998, Quieroz & El-Hani 2006, Rose 2016), in particular with regard to semiotic process and cosmogony. Exploring further the path opened by those researches, the present paper aims to clarify the theoretical problem of emergent evolution from a pragmatist perspective and especially to illustrate Peirce’s emergentist standpoint. In order to reach this goal, the article is divided into four parts: after (1) a brief introduction to the contemporary debates on emergence, (2) I give a historical overview of Classical Pragmatism and British Emergentists, (3) with a special focus on the common roots of the British Emergentists and Peirce on evolution. Finally, (4) I offer an emergentist reading of Peirce’s theory of evolution. In particular, I show how his strong emphasis on chance and the “growth” of the universe go together with his arch-stone of synechism (that is his theory of continuity), through what he calls agapasm.
C. S. Peirce and the Nested Continua Model of Religious Interpretation

Source: C. S. Peirce and the Nested Continua Model of Religious Interpretation
The writings of the American pragmatist thinker Charles S. Peirce (1839–1914) provide resources for a hermeneutical model called the nested continua model of religious interpretation. A diagrammatic demonstration of iconic relational logic akin to Peirce’s Existential Graphs, the nested continua model is rendered as a series of concentric circles graphed upon a two-dimensional plane. When faced with some problem of interpretation, one may draw discrete markings that signify that problem’s logical distinctions, then represent in the form of circles successive contexts by which these distinctions may be examined in relation to one another, arranged ordinally at relative degrees of specificity and vagueness, aesthetic intensity, and concrete reasonableness. Drawing from Peter Ochs’s Scriptural Reasoning model of interfaith dialogue and Robert C. Neville’s axiology of thinking—each of which makes creative use of Peirce’s logic—this project aims to achieve an analytical unity between these two thinkers’ projects, which can then be addressed to further theological ends. The model hinges between diagrammatic and ameliorative functions, honing its logic to disclose contexts in which its theological or metaphysical claims might, if needed, be revised. These are claims made from a particular identity in a particular cultural context, but the logical rules upon which the claims are based are accessible to all. The book’s aims are to reconcile Neville’s and Ochs’s insights, explore the means by which phenomenal experience becomes encoded in texts and practices, and expand the capacity for comparing the texts and practices of one community with those of another.
Source: C. S. Peirce and the Nested Continua Model of Religious Interpretation / Review Notre Dame
Gary Slater has produced a highly original and intellectually sophisticated argument intended to develop resources in Charles S. Peirce’s philosophy for the purposes of contemporary philosophical theology. Toward that end, Slater articulates a “nested continua model” for religious interpretation early in the book, one indebted to Peirce’s “Existential Graphs,” a system of diagrams designed to provide a visual representation of the process of human reasoning. Although it has been the subject of considerable discussion, nevertheless, very few scholars have developed practical applications for Peirce’s system of graphs. Peter Ochs is an exception, having adapted Peirce’s logic for specifically theological purposes in an important book published in 1998. One of the valuable secondary contributions of Slater’s project is his successful attempt to place Ochs’ “postliberal” deliberations in productive conversation with Robert Neville’s straightforwardly liberal theology. (Along with Robert Corrington and Hermann Deuser, Ochs and Neville have been the most prominent and influential contemporary theological interpreters of Peirce’s philosophy.) As a result, Slater is able to formulate a perspective that combines a nuanced historicism with a robust metaphysics — a combination rare enough to be noteworthy.
The complexities of the nested continua model are unpacked at some length early in the book, initially in the Introduction and then with greater detail toward the end of the first chapter. This model involves the use of inscriptions drawn on a two-dimensional graph, both as specific markings and as a series of concentric circles. On Slater’s account, the model can be used in a variety of ways. Inspired by Neville’s metaphysical speculations, a point marked at the center of the graph would represent “absolute firstness,” the creative source of everything determinate in the universe. Emanating from this point, a series of nested circles can be imagined as portraying realities further and further removed from the act of creation, so that eternity would be represented by the space beyond the outermost circle. Each circle is a continuum, nested within continua of greater generality and “emerging” from those more determinate realities that it enframes. Using the model to illustrate the very different kind of analysis with which Ochs is preoccupied, each circle can also be regarded as supplying an interpretive framework for understanding everything that it contains, even as each framework is itself rendered meaningful by the broader contexts in which it is embedded. Slater observes that any two things that might be distinguished from each other can be marked on the graph as “A” and “B”; any circle drawn around them (“C”) signifies a rule of reasoning useful for interpreting these things. “The power of the model,” Slater suggests, “consists in its claim that any problem or interpretive framework can be graphed, and that the logical form for doing so — ‘A’ relates to ‘B’ with respect to some ‘C’ — remains consistent across all levels of generality” (p. 13).
In the second chapter Slater delineates the intellectual resources from which the nested continua model was developed, most of them Peircean in origin. Some of the difficulty in fully evaluating Slater’s project can be linked to certain unresolved problems in Peirce’s philosophy. Although Slater’s model is inspired by Peirce’s Existential Graphs, it should be noted that Peirce began to develop that iconic system of logic only late in his career; when he died this work remained sketchy, the Gamma graphs (devoted to modal logic) having never been completed. Peirce’s logical deliberations, moreover, were informed by his study of the topology of Johann Listing, a 19th century mathematician whose approach to the subject differs dramatically from that of later 20th and 21st century topologists. Similarly, Peirce’s concept of the infinitesimal, appropriated by Slater for multiple purposes (including his account of how continua emerge one from another), was never fully developed, leaning on the earlier work of his father Benjamin and only vaguely anticipating the way in which this concept would later be employed by Abraham Robinson in his formulation of non-standard analysis (in the 1960’s). Surely Peirce’s investigations in logic, topology and the mathematics of the infinitesimal must be regarded as unfinished business.
It should be noted that Peirce regarded any two-dimensional graph as being inadequate for the purposes of his modal logic. For the Gamma system, not a single “sheet of assertion,” but rather a three-dimensional “book of sheets, tacked together at points” would be required. This conclusion is consistent with Peirce’s critique of Josiah Royce’s map metaphor, articulated in his review of the latter’s Gifford Lectures on The World and the Individual; that map would have to be conceived as only a “section” of some three-dimensional projection. Slater himself recognizes this limitation of his model, admitting that “change itself cannot be rendered on the graph, which is after all a two-dimensional space” (p. 103). His choice is to work within this limitation rather than attempt to develop the model, thus understanding change “in terms of infinitesimal emergence.” He further admits that this move involves leaning on a concept of “emergence” that “Peirce himself did not use” (p. 85).
Whatever the limitations of Slater’s nested continua model, the ingenuity displayed in his articulation of it is impressive. Moreover, he is careful to modestly circumscribe claims about its potential usefulness, insisting that its employment ought to be understood as only a starting point for any theological inquiry (p. 209). Early on, he describes it as “a kind of abductive Petri dish” for the purpose of testing various theological hypotheses (p. 75). It facilitates a process of experimental thinking and the clarification of vague ideas, especially in the early stages of inquiry. Rather than constituting a full-blown theological method, then, Slater envisions the graphing as playing a key but limited role in such a method.
On my evaluation, the general utility of the model (as with Peirce’s existential graphs) consists in its pronounced ability to direct attention for the purpose of making certain inferences (what Slater typically refers to as “willful awareness”), thus displaying the crucial role that attention plays in all forms of human reasoning. (Consider Slater’s insightful discussion of “Prescisive and Habit-Conditioned Reasoning” on pages 79-82 — although I think that Slater conflates “prescision” with “hypostatic abstraction” in a way that he might be more careful to avoid.) The iconic features of the model also enable Slater to avoid the pitfalls of what he refers to as “linguistic determinism” (p. 122); unlike certain contemporary neo-pragmatists, Slater is disinclined to reduce semiosis to language, or limit interpretation to verbal behavior.
With regard to particular uses of the model here, there are also some moments of extraordinary insight, highly original ideas that would be well worth developing. One consists in Slater’s use of the nested continua model as an analytical tool to safeguard against metaphysical absolutism or idolatry, playing on the contrast in the model between “translucent” and “opaque” circles of interpretation. Another, toward the end of the book, involves his establishing a link between love and “singular evil” via the Scotistic concept of haecceity (pp. 193-98); since both presuppose an awareness of the radically individual character of things it makes sense on his account to describe such evil as a kind of “love gone wrong.” This is nicely done. There are also tantalizing suggestions about a type of “Thirdness” that might be shown to function “as the ultimate logical interpretant with regard to prayer” (p. 157; although the promise to develop this suggestion in a later chapter is only partially redeemed).
However one might evaluate the virtues or shortcomings of Slater’s logical model, on my reading, the significance of this book can by no means be reduced to such an evaluation. For example, the discussion and critique of theological supersessionism is thoughtful and illuminating, even while it is not linked closely enough to the nested continua model to demonstrate how or even that the model is required for the purposes of this discussion. Slater’s recognition that theological reflection takes multiple forms and so cannot be reduced to a set of responses to problematic beliefs or situations mirrors his nuanced interpretation of Peirce’s philosophy. While careful to note that Peirce’s full-blown theory of inquiry is capacious enough to embrace both the early “stimulus of doubt” account and the later portrayal of musement, Slater wisely avoids driving any kind of deep wedge between Peirce’s initial pragmatism and his eventual “pragmaticism.” The summary of key intellectual influences on Peirce’s philosophy in the book’s first chapter is a model of clarity. And since Peirce wrote very little about the topic, Slater’s creative gesturing “Toward a Peircean Philosophy of History” in chapter three deserves careful consideration
As already indicated, Slater’s attempt to mediate between the contrasting philosophical and theological perspectives articulated by Ochs and Neville represents a significant achievement. His sensitive reading of these two important but sometimes neglected interpreters of Peirce is scattered throughout the book, but forms the bulk of chapters four and five. Ochs’ portrayal of “scriptural reasoning” as an historically conditioned mode of “repair” and Neville’s account of all human thought as being intrinsically and essentially “axiological” represent a challenging subject matter rendered lucid by Slater’s treatment.
Yet Slater’s attention is by no means limited to the work of these two figures. He provides perhaps the most comprehensive overview to date of the scholarly conversation devoted to Peirce’s relevance for theology and religious studies. This overview extends back to the pioneering labors of John E. Smith, includes discussion of Corrington’s “ecstatic naturalism” as well as my own investigations in “theosemiotic,” and then proceeds to incorporate insights gleaned from the work of a small group of younger scholars (such as Leon Niemoczynski, Anette Ejsing, Abraham Robinson and Brandon Daniel-Hughes) who are presently shaping that conversation in new and interesting ways. With the publication of this book, Gary Slater now occupies a prominent place in this latter group. His voice is an original one, his scholarly range impressive (so that his reading of pragmatism registers points of view as disparate as those of Robert Brandom and Sandra Rosenthal). The bold creativity of his model is likely to attract the attention of numerous readers. The insightful application of that model to important issues in the study of religion should both sustain and reward such attention.
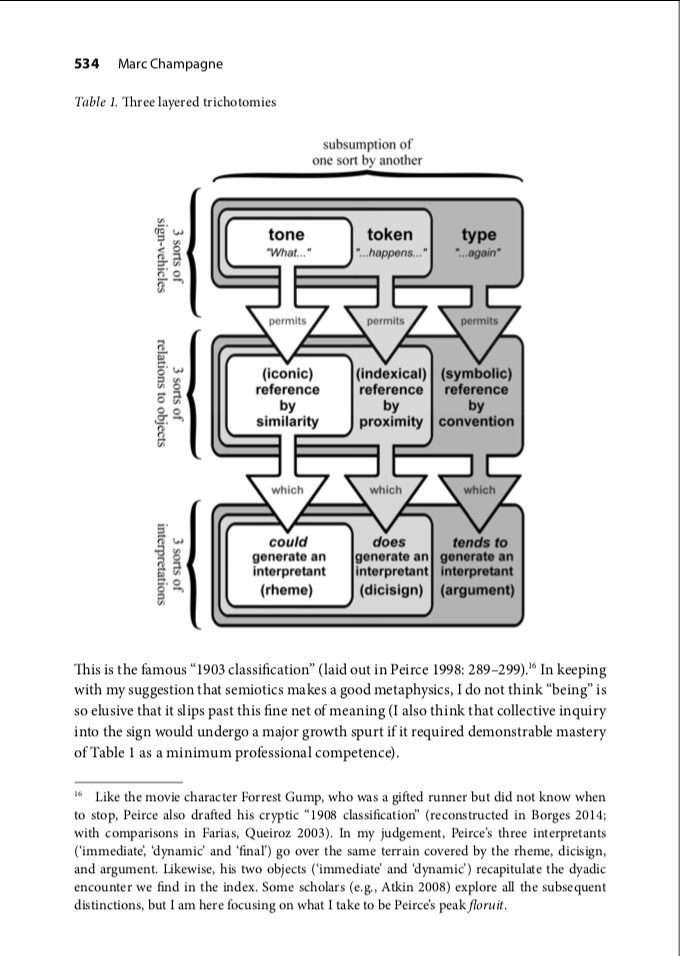
Source: A Visual Model of Peirce’s 66 Classes of Signs Unravels His Late Proposal of Enlarging Semiotic Theory

Source: A Less Simplistic Metaphysics: Peirce’s Layered Theory of Meaning as a Layered Theory of Being
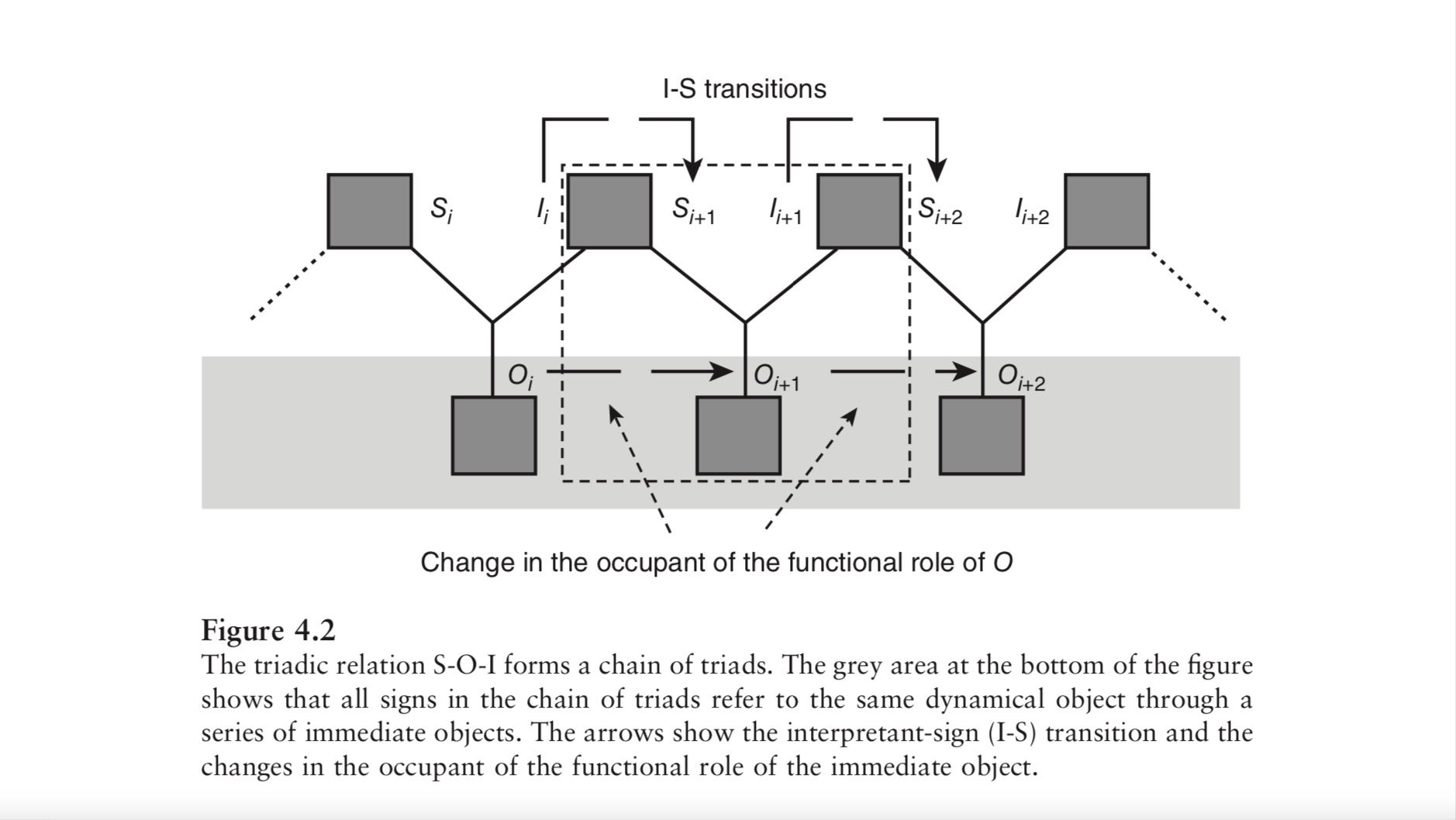
Source: PEIRCE’S CONTINUUM: A METHODOLOGICAL AND MATHEMATICAL APPROACH

Source: PEIRCE’S CONTINUUM: A METHODOLOGICAL AND MATHEMATICAL APPROACH
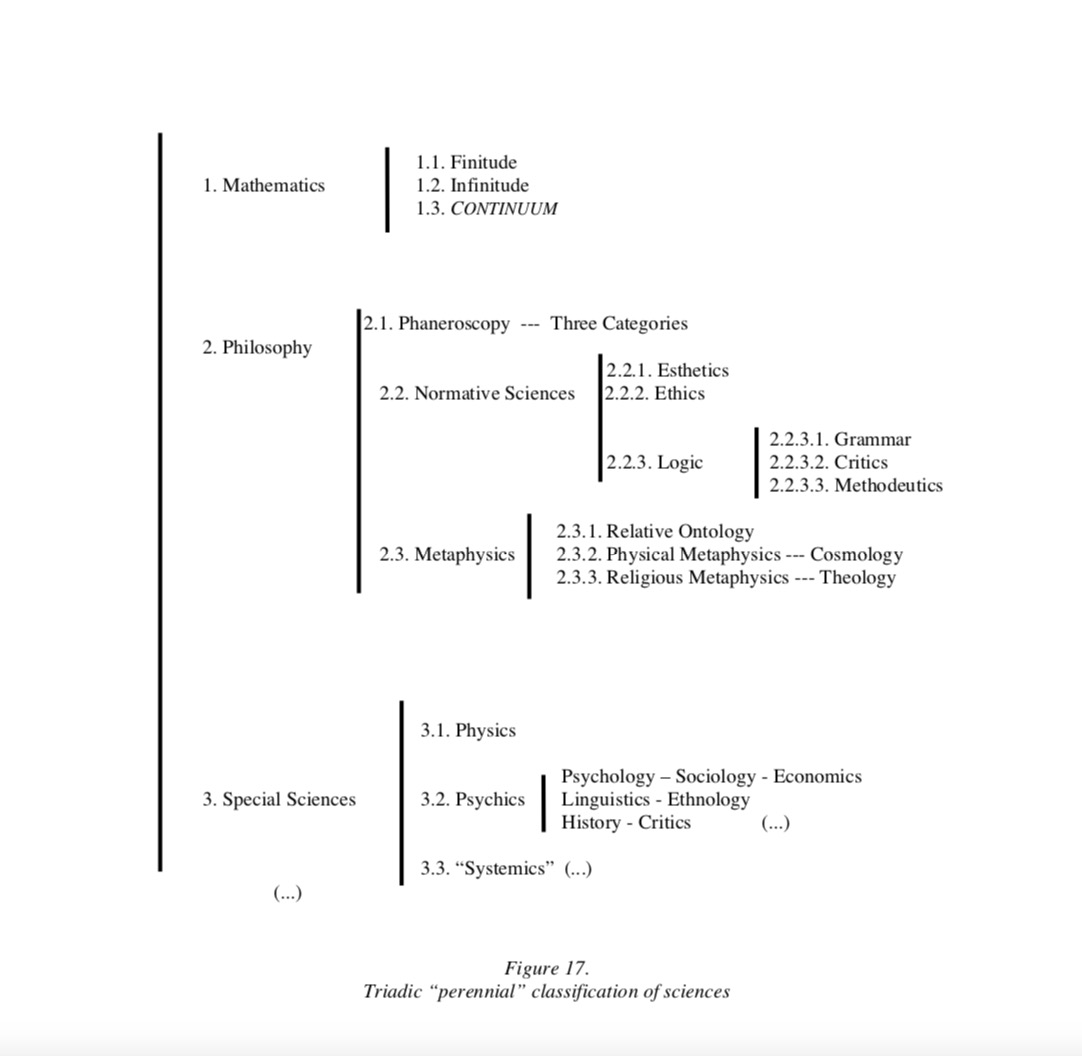
Source: PEIRCE’S CONTINUUM: A METHODOLOGICAL AND MATHEMATICAL APPROACH

Continuum East and West
THE CONTINUUM EAST AND WEST Peter G. Jones
Philosophy Pathways, 185, May 2014This essay examines the relationship between mysticism, for which Buddhism’s Middle Way doctrine would serve here as a defining example, and what, for want of better word, we call ‘Western’ philosophy. This is an issue of general interest to philosophers, since sooner or later in our investigations we must all decide whether the ‘Western’ kind of philosophy makes more or less sense to us than the ‘Eastern’ kind.
One obstacle we face in trying to make this decision is the difficulty of discerning clearly the defining characteristics of the two philosophies, those features that lead us to make such a final and definite distinction between them in the first place. We commonly speak of ‘Eastern’ and ‘Western’ philosophy, but are not so commonly able to say quite what we mean by this. The relevant issues are profound, mind-bending and probably inexhaustible. They need not be complicated, and they are often quite simple, but they are always immensely challenging.
One of these simple (stripped of the details) yet challenging issues would be the true nature of the continuum. The discussion that follows outlines the view of physicist, mathematician and philosopher Hermann Weyl. Weyl makes a careful distinction between the ‘arithmetical’ continuum, the continuum conceived of as an extended object, as it must be for the real numbers and space-time, and the ‘intuitive’ continuum, the empirical continuum of experience, which is not extended, and he demonstrates that when we set out to define what we mean by ‘Eastern’ and ‘Western’ philosophy, the foundations of analysis would be a good place to start. The interconnectedness of all the relevant issues at a foundational level, for all roads lead to Rome, means that we may as well start where we like, but mathematics takes us immediately to what might be the most clearly discernable and easily described difference between the two philosophies and worldviews, perhaps also the most general and profound, namely their entirely different conceptions of the continuum.
As there is just one source for each author quoted here I have not added numbered references but just tried to make it clear who is talking. Italics are always original.
>><<
In The Continuum: A Critical Examination of the Foundations of Analysis, Hermann Weyl points out that the extended space-time of physics and ordinary perception is, in the same way as the number line, a construction of reason and not intuitively or empirically given. He addresses a problem that arises in different guises but with an equal vengeance in religion, physics, mathematics and metaphysics. It is the problem of modelling a continuum as an extended series of discrete locations or ‘things’, as we do must do for the number line, geometry and arithmetic, space and time, and even for our very concept of the continuum, when a series of discrete locations or ‘things’ is exactly and precisely what a continuum is not.
A continuum cannot be extended as a series of points or moments for the reasons Weyl gives below, and yet it must be in order for anything to be extended in space and time. This causes a problem in philosophy. It would be a ‘first-order’ metaphysical problem or ‘antinomy’, a straight choice between two ideas neither of which work. It would be closely connected with the question of how many angels can dance on the head of a pin, of how small we can make an angel before it becomes the ‘ghost of a departed quantity’. The various problems and paradoxes to which the intellectually-constructed continuum of the arithmetical line gives rise has no impact on the usefulness of mathematics, which is wholly dependent on this conception, but it indicates that the continuum of space-time is not an equivalent case and is, rather, a true continuum. As such, it would not be a set of locations but a unity. A unity has no parts. This would suggest that space and time are conceptual imputations and that Reality, whatever is truly and independently-real amongst all the smoke and mirrors, is not in fact extended. This is a difficult idea but not a new one, and it is widely popular in religion. When theoretical physicists say ‘distance is arbitrary’, perhaps they are suggesting something similar. It might at least help to explain how a Big Bang can appear to have occurred before there is, was or ever will be a time or a place for it to have happened. For an ultimate view it would not have happened. If the continuum cannot have parts then all co-ordinate systems are emergent.
Here is Tobias Dantzig, a mathematician admired by Einstein, introducing the issues.
Herein I see the genesis of the conflict between geometrical intuition, from which our physical concepts derive, and the logic of arithmetic. The harmony of the universe knows only one musical form – the legato; while the symphony of numbers knows only its opposite, – the staccato. All attempts to reconcile this discrepancy are based on the hope that an accelerated staccato may appear to our senses as legato. Yet our intellect will always brand such attempts as deceptions and reject such theories as an insult, as a metaphysics that purports to explain away a concept by resolving it into its opposite.
While a series of points serves perfectly well for the continuum of the number line and arithmetic, on examination it is a paradoxical idea that must be rejected in both metaphysics and physics as a model of space-time. The continuum of physics is, at this time, extended as a series of points and moments, and as such no sense can be made of it. Viewed as a real phenomenon a continuum so-defined would either be paradoxical or fail to qualify for the name. We have every right to define the continuum for mathematics as we currently do, and if our idea is paradoxical then it is only a problem when we investigate the foundations of analysis. When we define the continuum for mathematics we are not making a claim about the nature of Reality. Elsewhere it would be a different matter. In metaphysics we certainly cannot adopt a priori an arithmetical definition of the continuum. Insofar as it relates to metaphysics this might be the central message of Weyl’s book. At the same time, physics and ordinary perception are heavily theory-laden, dangerously so. Our usual everyday theory is that time and space are extended in just the same way as is the number line, such that space- and time-points can be represented as locations in an extended co-ordinate system. But is there any evidence that space and time are extended objects? What is it that our wristwatch is actually measuring? Are we quite sure that our usual theory of extension, for which space-time would be a ‘classical’ or Newtonian phenomenon, is fundamentally correct? Is it a metaphysical conjecture, a testable scientific theory, something we know from experience or a highly evolved misinterpretation? For our Western tradition of philosophy this would be a famously undecidable problem. Here the continuum appears to be paradoxical, for it cannot be extended ex hypothesis, and yet, by some magic, it is. Or it seems to be. For the Eastern tradition this everyday theory of space-time would be testable and it would fail the tests, being refutable in logic and falsifiable in experience. The continuum would be a unity, just as its name implies.
Weyl reduces the conceptually extended continuum of mathematics and traditional physics to what he calls the ‘true’ or ‘intuitive’ continuum, where the latter is carefully distinguished from the former. The intuitive continuum, the continuum as we experience it, is not extended as a series of moments or points. We do not experience time and space as consisting of moments and points, or, if we do, it is only ever the same moment and point. We are always here and now. What is more, there is actually something very odd about the idea that space and time are ‘grainy’ in this way. The length of ten thousand points would be equal to the length of one point, for a start, so no amount of points would be sufficient to construct basic geometry, let alone a piano. In the same way, no amount of moments would be sufficient to account for motion and change. Space and time are explanatory theories, Weyl proposes, generated by reason and imagination, not empirical phenomena.
For an orthodox view of space-time here is a passage from Wikipedia from the entry for Hermann Minkowsky.
This new reality was that space and time, as physical constructs, have to be combined into a new mathematical/physical entity called ‘space-time’, because the equations of relativity show that both the space and time coordinates of any event must get mixed together by the mathematics, in order to accurately describe what we see. Because space consists of 3 dimensions, and time is 1- dimensional, space-time must, therefore, be a 4-dimensional object. It is believed to be a ‘continuum’ because so far as we know, there are no missing points in space or instants in time, and both can be subdivided without any apparent limit in size or duration. So, physicists now routinely consider our world to be embedded in this 4-dimensional Space-Time continuum, and all events, places, moments in history, actions and so on are described in terms of their location in Space-Time.
Dantzig explores the origins of this co-ordinate system.
The notion of equal-greater-less precedes the number concept. We learn to compare before we lean to evaluate. Arithmetic does not begin with numbers; it begins with criteria. Having learnt to apply these criteria of equal-greater-less, man’s next step was to devise models for each type of plurality. These models are deposited in his memory very much as the standard meter is deposited at the Bureau of Longitudes in Paris. One, two, three, four, five …; we could just as well have said: I,
wings, clover, legs, hand … and, for all we know, the latter preceded our present form.
He goes on to observe that the staccato of the numbers is not empirical or intuitive, but a superimposition.
It is possible to assign to any point on a line a unique real number, and, conversely, any real number can be represented in a unique manner by a point on the line.
This is the famous Dedekind-Cantor axiom. This proposition, by sanctifying the tacit assumption on which analytical geometry had operated for over two hundred years, became the fundamental axiom of this discipline. It defines a new mathematical being, the arithmetical line. Henceforth the line – and consequently the plane, and space – ceases to be an intuitive notion and is reduced to being a mere carrier of numbers.
In the following passage Dantzig notes the paradoxical nature of the arithmetical line. This matters little in mathematics, but when the arithmetical line is taken to be a model of the true continuum it renders Reality paradoxical and causes philosophical havoc, in particular a deep rift between two quite different traditions of philosophy.
The axiom of Dedekind – “if all points of a straight line fall into two classes, such that every point of the first class lies to the left of any point of the second class, then there exists one and only one point which produces this division of all points into two classes, this severing of the straight line into two portions” – this axiom is just a skilful paraphrase of the fundamental property we attribute to time. Our intuition permits us, by an act of the mind, to sever all time into the two classes, the past and the future, which are mutually exclusive and yet together comprise all of time, eternity: The now is the partition which separates all the past from all the future; any instant of the past was once a now, any instant of the future will be a now anon, and so any instant may itself act as such a partition. To be sure, of the past we know only disparate instants, yet, by an act of the mind we fill out the gaps; we conceive that between any two instants – no matter how closely these may be associated in our memory – there were other instants, and we postulate the same compactness for the future. This is what we mean by the flow of time.
Furthermore, paradoxical though this may seem, the present is truly irrational in the Dedekind sense of the word, for while it acts as partition it is neither a part of the past nor a part of the future. Indeed, in an arithmetic based on pure time, if such an arithmetic was at all possible, it is the irrational which would be taken as a matter of course, while all the painstaking efforts of our logic would be directed toward establishing the existence of rational numbers.
In other words, the Dedekind sense of the word ‘present’ is irrational. Space-time cannot have the properties he assigns to the number line unless the Cosmos is irrational. This is the problem addressed by Weyl. He deals with it by making a clear distinction between the intuitive or experienced continuum, the intuition of the continuum that for all of us is an empirical phenomenon, and the intellectually constructed faux-continuum of Dedekind’s arithmetical line. They could hardly be more different.
To the criticism that the intuition of the continuum in no way contains those logical principles on which we must rely for the exact definition of the concept “real number,” we respond that the conceptual world of mathematics is so foreign to what the intuitive continuum presents to us that the demand for coincidence between the two must be dismissed as absurd.
He points out that the usefulness of the arithmetical line has no bearing on its plausibility as a model of the space-time continuum.
Whichever view of the relation of mathematics to nature one takes, there is no independent physical conception of the continuum on offer in all this, since all the mathematics is filtered through the real number system (or Hilbertian geometry as a surrogate). Moreover, I don’t see that any argument can be made from the enormously successful applications of mathematics in natural science to the conclusion that one or another of the mathematical conceptions of the continuum surveyed above is uniquely singled out as the “real one”. In any case, the work on the reach of predicative mathematics cited at the end of the preceding section shows that the properties of the continuum needed for its applications in natural science do not require it to have a definite reality in the platonistic sense.
Here is extract from an essay on Weyl and the continuum by John Bell.
…Weyl regards the experienced continuous flow of phenomenal time as constituting an insuperable barrier to the whole enterprise of representing this continuum in terms of individual points, and even to the characterization of “individual temporal point” itself. As he says,
“The view of a flow consisting of points and, therefore, also dissolving into points turns out to be mistaken: precisely what eludes us is the nature of the continuity, the flowing from point to point; in other words, the secret of how the continually enduring present can continually slip away into the receding past.
Each one of us, at every moment, directly experiences the true character of this temporal continuity. But, because of the genuine primitiveness of phenomenal time, we cannot put our experiences into words. So we shall content ourselves with the following description. What I am conscious of is for me both a being-now and,
in its essence, something which, with its temporal position, slips away. In this way there arises the persisting factual extent, something ever new which endures and changes in consciousness.”
We see here that an examination of the foundations of analysis leads us immediately into the realms of psychology, physics, metaphysics, religion, consciousness studies and more. Bell continues.
Weyl sums up what he thinks can be affirmed about “objectively presented time”— by which I take it he means “phenomenal time described in an objective manner”— in the following two assertions, which he claims apply equally, mutatis mutandis, to every intuitively given continuum, in particular, to the continuum of spatial extension:
1. An individual point in it is non-independent, i.e., is pure nothingness when taken by itself, and exists only as a “point of transition” (which, of course, can in no way be understood mathematically);
2. It is due to the essence of time (and not to contingent imperfections in our medium) that a fixed temporal point cannot be exhibited in any way, that always only an approximate, never an exact determination is possible.
The fact that single points in a true continuum “cannot be exhibited” arises, Weyl continues, from the fact that they are not genuine individuals and so cannot be characterized by their properties. In the physical world they are never defined absolutely, but only in terms of a coordinate system, which, in an arresting metaphor, Weyl describes as “the unavoidable residue of the eradication of the ego.”
In particular, he found compelling the fact that the Brouwerian continuum is not the union of two disjoint nonempty parts— that it is, in a word, indecomposable. “A genuine continuum,” Weyl says, “cannot be divided into separate fragments.” In later publications he expresses this more colourfully by quoting Anaxagoras to the effect that a continuum “defies the chopping off of its parts with a hatchet.”
Weyl’s book on the continuum delves little further into metaphysical issues than is necessary for his examination of analysis. Elsewhere he says more, and we find a clear connection between his mathematico-philosophical views and Buddhism’s theory of emptiness and doctrine of dependent origination. As far as it goes his book on the continuum could be read as a mathematical explanation of the universe of the perennial philosophy, and of how it differs from that of the Western tradition in at least one vital respect. Bell makes the correlation clear.
In The Open World (1932), Weyl provides an eloquent formulation of his philosophical outlook, which quickly moves beyond its initial echoes of Schopenhauer:
“The beginning of all philosophical thought is the realization that the perceptual world is but an image, a vision, a phenomenon of our consciousness; our consciousness does not directly grasp a transcendental real world which is as it appears. The tension between subject and object is no doubt reflected in our conscious acts, for example, in sense perceptions. Nevertheless, from the purely epistemological point of view, no objection can be made to a phenomenalism which would like to limit science to the description of what is “immediately given to consciousness”. The postulation of the real ego, of the thou and of the world, is a metaphysical matter, not judgment, but an act of acknowledgment and belief.
But this belief is after all the soul of all knowledge. It was an error of idealism to assume that the phenomena of consciousness guarantee the reality of the ego in an essentially different and somehow more certain way than the reality of the external world; in the transition from consciousness to reality the ego, the thou and the world rise into existence indissolubly connected and, as it were, at one stroke.”
Any comparison of ‘Eastern’ and ‘Western’ approaches to philosophy must eventually end up here, examining the question of whether the continuum of space-time is arithmetical and paradoxical, or whether it would make more sense to say that spatio-temporal extension is an interpretation of appearances, a relationship between appearances, and not an empirical or even truly real phenomenon. Whichever way we decide this question, an examination of these issues will reveal a clear and crucial difference of opinion between East and West over the ultimate nature of Reality.
It is absurdly misleading to use the words ‘Western’ and ‘Eastern’ to describe two philosophical camps, and really it is dualism and nondualism that we are comparing here, both of which appear all over the world. Whatever words we use, mathematics can help us to pin down our definitions in important respects.
Weyl summarises his view as follows.
The category of the natural numbers can supply the foundation of a mathematical discipline. But perhaps the continuum cannot, since it fails to satisfy the requirements [mentioned in Chapter1]: as basic a notion as that of the point in the continuum lacks the required support in intuition. It is to the credit of Bergson’s philosophy to have pointed out forcefully this deep division between the world of mathematical concepts
and the immediately experienced continuity of phenomenal time.
The view of a flow consisting of points and, therefore, also dissolving into points turns out to be false. Precisely what eludes us is the nature of the continuity, the flowing from point to point; in other words, the secret of how the continually enduring present can continually slip away into the receding past….
…When our experience has turned into a real process in a real world and our phenomenal time has spread itself out over this world and assumed a cosmic dimension, we are not satisfied with replacing the continuum by the exact concept of the real numbers, in spite of the essential and undeniable inexactness arising from what is given. For, as always, there is more at work here than heavy-handed schematizing or cognitive economizing devised for fulfilling our practical tasks and objectives. Here we discover genuine reason which lays bare the “Logos” dwelling in reality (just as purely as is possible for this consciousness which cannot “leap over its own shadow”). But to discuss this further cannot be our business here. Certainly, the intuitive and the mathematical continuum do not coincide; a deep chasm is fixed between them….
…The reflections contained in this section are, of course, only a slightly illuminating surrogate for a genuine philosophy of the continuum. But since no penetrating treatment of this topic is at hand and since our task is mathematical rather than epistemological, the matter can rest there.
For a book on analysis it would have been inappropriate for Weyl to say more about this. If we are examining the pivotal questions on which Eastern and Western philosophies are divided, however, then the matter cannot rest here. The former philosophy makes a claim about the continuum that is denied point-blank by the latter. It may still be true that ‘no penetrating treatment of this topic is at hand’, at least outside of the ‘mystical’ literature, but this would not reflect on the importance of this topic across all of philosophy, and it need not prevent us from forming a view on which of these two philosophical approaches gives the most plausible description of space and time.
Is space-time extended or is it a continuum? Weyl suggest that we cannot have it both ways. Nagarjuna’s Middle Way Buddhism, which is infuriatingly stubborn when it comes to endorsing extreme views on any topic, would say that the question is not quite answerable in this straightforward form. There would be a sense in which it is neither and a sense in which it is both. There is not a straightforward disagreement between East and West on the answer to this question, therefore, with the two sides adopting equal and opposite views. All the same, it seems true to say that the very different answers they give to this question reveal one of the most crucial and far-reaching differences between these two traditions of philosophical thought.
Bibliography
Bell, John L, ‘Hermann Weyl on intuition and the continuum’.
Click to access Hermann%20Weyl.pdf
Dantzig, Tobias, Number – The Language of Science, (Pearson Education 2005 (1930)
Weyl, Hermann, The Continuum: A Critical Examination of the Foundations of Analysis, Dover (1987)
My Related Posts
Charles Sanders Peirce’s Visual Logic: Diagrams and Existential Graphs
Charles Sanders Peirce’s Theory of Signs
The Aesthetics of Charles Sanders Peirce
Indra’s Net: On Interconnectedness
Maha Vakyas: Great Aphorisms in Vedanta
Key Sources of Research
Implications of Synechism: Continuity and Second-Order Vagueness
Implicações do Sinequismo: Lógica Triádica e Vagueza de Segunda Ordem
Marco Annoni
Università di Pisa – Italia
marcoabrema@hotmail.com
COGNI TI O-ESTUDOS: Revista Eletrônica de Filosofia
Centro de Estudos do Pragmatismo – Programa de Estudos Pós-Graduados em Filosofia – Pontifícia Universidade Católica de São Paulo
São Paulo, Volume 3, Número 2, p. 096- 108, TEXTO 11/3.2, julho/dezembro, 2006
https://www.academia.edu/1965259/Implications_of_Synechism_Continuity_and_Second_Order_Vagueness
Continuity as vagueness: The mathematical antecedents of Peirce’s semiotics*
PETER OCHS
Semiotica 96-3/4 (1993), 231-255 0037-1998/93/0096-0231
Peirce and Brouwer
Conor Mayo-Wilson
September 5, 2011
https://www.academia.edu/954648/Peirce_and_Brouwer
Peirce, Leibniz, and the threshold of pragmatism
Francesco Bellucci
Semiotica 2013; 195: 331 – 355
DOI 10.1515/sem-2013-0030
Dynamical Interpretation of Leibniz’s Continuum
Vassil VIDINSKY*
Peirce and Leibniz on Continuity and the
Continuum
D. A. Anapolitanos and D. Christopoulou*
*Corresponding author: D. Christopoulou, Assistant Professor Mathematics Department, Kapodistrian University of Athens, Athens, Greece, E-mail: chrdemet@yahoo.gr
D. A. Anapolitanos, History and Philosophy of Science Department, National and Kapodistrian University of Athens, Athens, Greece, E-mail: danap@phs.uoa.gr
Metaphysica 2020; aop
https://doi.org/10.1515/mp-2019-0008
Peirce’s Topological Concepts
Jérôme Havenel
Draft version of the book chapter published in
New Essays on Peirce’s Philosophy of Mathematics,
Matthew E. Moore ed, Open Court, 2010
Peirce’s Logic of Continuity
A Conceptual and Mathematical Approach
Fernando Zalamea
Book
https://www.academia.edu/31948393/ZalameaPeirceCont_pdf
Peirce’s Clarifications of Continuity
Jérôme Havenel
Transactions of the Charles S. Peirce Society: A Quarterly Journal
in American Philosophy, Volume 44, Number 1, Winter 2008,
pp. 86-133 (Article)
Published by Indiana University Press
DOI: 10.1353/csp.0.0001
https://www.researchgate.net/publication/236774797_Peirce%27s_Clarifications_of_Continuity
«Peirce’s meditations on continuity: from transitivity to topology»,
Havenel, J. (2015).
en: Zalemea, Fernando y Oostra, Arnold (eds).
Cuadernos de Sistemática Peirceana. Vol. 7,. Bogotá: Editorial Nomos, pp. 101-126.
Peirce’s Continuous Predicates
FRANCESCO BELLUCCI
Transactions of the Charles S Peirce Society
A Quarterly Journal in American Philosophy · April 2013
DOI: 10.2979/trancharpeirsoc.49.2.178
https://www.researchgate.net/publication/259734578_Peirce%27s_Continuous_Predicates
“Peirce’s Definitions of Continuity”
Potter, V. G.; Shields, S. J. (1977):
Transactions of the Charles Sanders Peirce Society, v. 13, n. 1, pp. 20-34.
Synechism: the Keystone of Peirce’s Metaphysics
Joseph Esposito
http://www.commens.org/encyclopedia/article/esposito-joseph-synechism-keystone-peirce’s-metaphysics
Peirce’s Logic of continuity: a conceptual and mathematical approach to the continuum and the existential graphs.
Zalamea, F. (2012).
Boston: Docent Press.
«Leibniz on Continuity»,
Arthur, R. (1986).
en: Proceedings of the Biennial Meeting of the Philosophy of Science, Science Association, Vol. 1986, Volume One: Contributed Papers, pp. 107-115
«Continuity in Leibniz’s Mature Metaphysics»,
Crockett, T. (May, 1999).
en: Philosophical Studies: An International Journal for Philosophy in the Analytic Tradition, Vol. 94, No. 1/2, Selected Papers Presented at the American Philosophical Association Pacific Division Meeting 1998, pp. 119-138.
«Peirce and Leibniz»,
Fisch, M. (Jul.-Sep. 1972).
en: Journal of the History of Ideas. Vol. 33, No. 3, Festschrift for Philip P. Wiener, pp. 485-496
The idea of continuity in the philosphies of Leibniz and Peirce.
Flórez Restrepo, J. A., & Arias Cardona, J. E. (2022).
Pensamiento. Revista De Investigación E Información Filosófica, 78(298 S. Esp), 841-861. https://doi.org/10.14422/pen.v78.i298.y2022.030
https://revistas.comillas.edu/index.php/pensamiento/article/view/10977
“On Peirce’s Discovery of Cantor’s Theorem.”
Moore, Matthew E. 2007.
Cognitio 8: 223–48.
“Peirce’s Cantor.”
Moore, Matthew E. 2011.
in New Essays on Peirce’s Mathematical Philosophy, ed. Matthew E. Moore. Chicago: Open Court.
“Peirce on Cantor’s Paradox and the Continuum.”
Myrvold, Wayne C. 1995.
Transactions of the Charles S. Peirce Society 31 (3): 508–41.
PATTERNHOOD, CORRELATION, AND GENERALITY: FOUNDATIONS OF A PEIRCEAN THEORY OF PATTERNS
Jimmy Jericho Aames
Master of Arts Thesis
in the Department of Philosophy
Indiana University
July 2016
https://scholarworks.iupui.edu/bitstream/handle/1805/10896/Thesis%2007052016.pdf?sequence=1
Peirce-Related Papers
Bibliography
Indiana University
https://arisbe.sitehost.iu.edu/menu/library/aboutcsp/ABOUTCSP.HTM
Charles Sanders Peirce
Wikipedia
https://en.wikipedia.org/wiki/Charles_Sanders_Peirce
Peirce’s “Extreme” Realism and Supermultitudinous Conception of Continuity
Jimmy Aames
Indiana University-Purdue University Indianapolis
Department of Philosophy MAE-mail: jjaames@iupui.edu
2015
Peirce on Continuity: Vindication of Universals against Nominalism
Paniel Reyes Cardenas
2014, Hannah, Patricia (Ed),An Anthology of Philosophical Studies 8
https://www.academia.edu/7005464/Peirce_on_Continuity_Vindication_of_Universals_against_Nominalism
Mathematical Structuralism, Continuity and Peirce’s Diagrammatic Reasoning
Paniel Reyes Cardenas
Bateson and Peirce on the Pattern that Connects and the Sacred
2008, A Legacy for Living Systems
https://www.academia.edu/725104/Bateson_and_Peirce_on_the_Pattern_that_Connects_and_the_Sacred
Philosophy of Mathematics
Selected Writings
Charles S. Peirce
Edited by
Matthew E. Moore
INDIANA UNIVERSITY PRESS 2010
Bloomington and Indianapolis
Peirce and the Continuum from a Philosophical Point of View.
Zink, J. (2001).
In: Schuster, P., Berger, U., Osswald, H. (eds) Reuniting the Antipodes — Constructive and Nonstandard Views of the Continuum. Synthese Library, vol 306. Springer, Dordrecht.
https://doi.org/10.1007/978-94-015-9757-9_25
https://link.springer.com/chapter/10.1007/978-94-015-9757-9_25
Peirce’s Topical Continuum: A “Thicker” Theory
Jon Alan Schmidt
TRANSACTIONS OF THE CHARLES S. PEIRCE SOCIETY Vol. 56, No. 1 (2020) • doi: 10.2979/trancharpeirsoc.56.1.04
https://philarchive.org/archive/SCHPTC-2
Charles Sanders Peirce and the Principle of Bivalence
Robert Lane
1998
https://www.academia.edu/660658/Charles_Sanders_Peirce_and_the_Principle_of_Bivalence
The genesis of the Peircean continuum
Matthew E. Moore
Transactions of the Charles S. Peirce Society 43 (3):425 – 469 (2007)
Peirce’s topical theory of continuity.
Moore, Matthew E. (2015).
Synthese 192 (4):1-17.
Peirce’s Triadic Logic Revisited
Lane, Robert (1999).
Transactions of the Charles S. Peirce Society 35 (2):284 – 311.
Peirce’s Graphs—The Continuity Interpretation.
Zeman, J. Jay (1968).
Transactions of the Charles S. Peirce Society 4 (3):144 – 154.
Peirce on Continuity and Laws of Nature.
Sfendoni-Mentzou, Demetra (1997).
Transactions of the Charles S. Peirce Society 33 (3):646 – 678.
Questions concerning Peirce’s Agapic Continuity.
Staab, Janice M. (1999).
Transactions of the Charles S. Peirce Society 35 (1):157 – 176.
Peirce’s Definitions of Continuity and the Concept of Possibility.
Noble, N. A. Brian (1989).
Transactions of the Charles S. Peirce Society 25 (2):149 – 174.
Peirce’s Potential Continuity and Pure Geometry.
Hudry, Jean-Louis (2004).
Transactions of the Charles S. Peirce Society 40 (2):229 – 243.
The Continuity of Peirce’s Thought.
Colapietro, Vincent (1999).
The Personalist Forum 15 (2):432-437.
Continuity and Inheritance: Kant’s “Critique of Judgment” and the Work of C. S. Peirce.
Kaag, John (2005).
Transactions of the Charles S. Peirce Society 41 (3):515 – 540.
Peirce’s evolutionary logic: Continuity, indeterminacy, and the natural order.
Alborn, Timothy L. (1989).
Transactions of the Charles S. Peirce Society 25 (1):1 – 28.
Peirce’s mathematical-logical approach to discrete collections and the premonition of continuity.
Rebello Cardoso, Helio (2012).
Journal of Applied Non-Classical Logics 22 (1-2):11-28.
The Peircean Continuum
Vargas, Francisco, and Matthew E. Moore,
in Stewart Shapiro, and Geoffrey Hellman (eds), The History of Continua: Philosophical and Mathematical Perspectives (Oxford, 2020; online edn, Oxford Academic, 17 Dec. 2020), https://doi.org/10.1093/oso/9780198809647.003.0014, accessed 31 Mar. 2023.
The History of Continua: Philosophical and Mathematical Perspectives
Shapiro, Stewart, and Geoffrey Hellman (eds),
(Oxford, 2020; online edn, Oxford Academic, 17 Dec. 2020), https://doi.org/10.1093/oso/9780198809647.001.0001, accessed 31 Mar. 2023.
Peirce’s Topological Concepts
Jérôme Havenel
Draft version of the book chapter published in New Essays on Peirce’s Philosophy of Mathematics, Matthew E. Moore ed, Open Court, 2010.
https://www.academia.edu/25930950/Peirces_Topological_Concepts_Jerome_Havenel
A Category-Theoretic Reading of Peirce’s System: Pragmaticism, Continuity, and Existential Graphs.
Zalamea, Fernando. 2010.
In New Essays on Peirce’s Mathematical Philosophy, edited by Matthew E. Moore, pp. 203–233. Chicago: Open Court.
STEVIN NUMBERS AND REALITY
KARIN USADI KATZ AND MIKHAIL G. KATZ
2012
DISSERTATIONS ON PEIRCE
Indiana University
https://arisbe.sitehost.iu.edu/rsources/dissabs/diss.htm
The Continuum:
History, Mathematics, and Philosophy
by
Teppei Hayashi
A THESIS
DOCTOR OF PHILOSOPHY
GRADUATE PROGRAM IN PHILOSOPHY
UNIVERSITY OF CALGARY
CALGARY, ALBERTA December, 2017
New Essays on Peirce’s Mathematical Philosophy
Matthew E. Moore (ed.), New Essays on Peirce’s Mathematical Philosophy, Open Court, 2010, ISBN 9780812696813.
PEIRCE’S CONTINUUM
A METHODOLOGICAL AND MATHEMATICAL APPROACH
FERNANDO ZALAMEA
“Modern Topology and Peirce’s Theory of the Continuum.”
Johanson, Arnold.
Transactions of the Charles S. Peirce Society 37, no. 1 (2001): 1–12. http://www.jstor.org/stable/40320822.
C. S. Peirce and the Nested Continua Model of Religious Interpretation
Slater, Gary
Oxford Theology and Religion Monographs (Oxford, 2015; online edn, Oxford Academic, 17 Dec. 2015), https://doi.org/10.1093/acprof:oso/9780198753230.001.0001, accessed 2 Apr. 2023.
True Continuity and Analytical Continuity
In Continuity, discontinuity and negotiation of meaning in distributed virtual environments
Patrick John Coppock
https://arisbe.sitehost.iu.edu/menu/library/aboutcsp/coppock/Solomon/Solomon-True.html
C. S. Peirce and the Nested Continua Model of Religious Interpretation
Gary Slater, C. S. Peirce and the Nested Continua Model of Religious Interpretation, Oxford University Press, 2015, 242pp., $110.00 (hbk), ISBN 9780198753230.
Reviewed by Michael L. Raposa, Lehigh University
2016.06.07
Notre Dame Philosophical Reviews
Department of Philosophy
100 Malloy Hall
Notre Dame, IN 46556 USA
ndpr@nd.edu
https://ndpr.nd.edu/reviews/c-s-peirce-and-the-nested-continua-model-of-religious-interpretation/
On the relations between Georg Cantor and Richard Dedekind.
Ferreirós, J. (1993).
Historia Mathematica, 20, 343-363.
“The mathematical continuum: A haunting problematic,”
de Freitas, Liz (2018)
The Mathematics Enthusiast: Vol. 15 : No. 1 , Article 9.
DOI: https://doi.org/10.54870/1551-3440.1421
Available at: https://scholarworks.umt.edu/tme/vol15/iss1/9
Continuity and infinitesimals.
Bell, J.L. (2013).
Stanford Encyclopedia of Philosophy.
https://plato.stanford.edu/entries/continuity/
The continuous, the discrete and the infinitesimal in philosophy and mathematics.
John L. Bell
Switzerland: Springer, 2019, 313+xvii pp,
The Continuous and the Infinitesimal in Mathematics and Philosophy
John Lane Bell
Polimetrica s.a.s., 2005
The Continuum and the Evolution of the Concept of Real Number
John L. Bell
Department of Philosophy
The University of Western Ontario
jbell@uwo.ca
Varieties of Continua: From Regions to Points and Back.
Hellman, G, and S. Shapiro (2018).
Oxford University Press.
The Continuous and the Discrete: Ancient Physical Theories from a Contemporary Perspective
White, M. J. (1992).
Clarendon Press, Oxford.
Varieties of Synechism: Peirce and James on Mind–World Continuity.
Calcaterra, Rosa M. (2011).
Journal of Speculative Philosophy 25 (4):412-424.
Review of Gary Slater, C. S. Pierce and the Nested Continua Model of Religious Interpretation
C. S. Peirce and the Nested Continua Model of Religious Interpretation. Gary Slater. Oxford: Oxford University Press, 2015. 242 pp.
Brandon Daniel-Hughes
John Abbott College
THE JOURNAL OF SCRIPTURAL REASONING
The Continuity of Continuity:
A Theme in Leibniz, Peirce and Quine
Begoña Ilarregui y Jaime Nubiola
Universidad de Navarra
Publicado en Leibniz und Europa, VI. Internationaler Leibniz-Kongress, 361-371.
Gottfried-Wilhelm-Leibniz-Gesellschaft e. V. Hannover., 1994.
https://www.unav.es/users/Articulo13.html
THE ABSOLUTE ARITHMETIC CONTINUUM AND THE UNIFICATION OF ALL NUMBERS GREAT AND SMALL
PHILIP EHRLICH
The Bulletin of Symbolic Logic
Volume 00, Number 0, XXX 0000
DIVERGENT CONCEPTIONS OF THE CONTINUUM IN 19TH AND EARLY 20TH CENTURY MATHEMATICS AND PHILOSOPHY
JOHN L. BELL
Towards a classifification of continuity and on the emergence of generality
Daniel Rosiak
DePaul University, drosiak@depaul.edu
Department of Philosophy
College of Liberal Arts and Social Sciences DePaul University
Chicago,IL
December, 2019
PEIRCE’S PLACE IN MATHEMATICS
BY JOSEPH W. DAUBEN
DEPARTMENT OF HISTORY, HERBERT H. LEHMAN COLLEGE, AND
Ph.D. PROGRAM IN HISTORY, THE GRADUATE CENTER,
THE CITY UNIVERSITY OF NEW YORK, NEW YORK, NY 10036
HISTORIA MATHEMATICA 9 (1982) 311-325
CONTEMPORARY INFINITESIMALIST THEORIES OF CONTINUA AND THEIR LATE 19TH- AND EARLY 20TH-CENTURY FORERUNNERS
PHILIP EHRLICH
‘One, Two, Three:Fundamental Categories of Thought and Nature,
Charles Sanders Peirce
Three Infinitesimalist Theories of Continua
Philip Ehrlich
“The Absolute Arithmetic Continuum and its Peircean Counterpart”
P . Ehrlich,
in New Essays on Peirce’ s Mathematical Philosophy, edited by Matthew Moore, Open Court Press (forthcoming).
Charles S. Peirce’s Idea of Ultimate Reality and Meaning Related to Humanity’s Ultimate Future as seen through Scientific Inquiry
Noel E. Boulting, Mid-Kent College o fHigher and Further Education, Chatham, Kent, England
https://www.utpjournals.press/doi/pdf/10.3138/uram.16.1-2.9
THE SACRED DEPTHS OF NATURE
AN ONTOLOGY OF THE POSSIBLE IN THE PHILOSOPHY OF PEIRCE AND HEIDEGGER
Leon J. Niemoczynski
B.A., East Stroudsburg University, 2001 M.A., West Chester University, 2004
Department of Philosophy
in the Graduate School Southern Illinois University Carbondale May 2009
The Completeness of the Real Line
Matthew E. Moore
Department of Philosophy, Brooklyn College. E–mail: matthewm@brooklyn.cuny.edu
Crítica (Méx., D.F.) vol.39 no.117 Ciudad de México dic. 2007
“Logique et mathématique du Continu chez Charles Sanders Peirce”,
Havenel, Jérôme, 2006,
Doctoral Thesis, École des Hautes Études en Sciences Sociales, Paris.
https://www.theses.fr/2006EHES0079
A Less Simplistic Metaphysics: Peirce’s Layered Theory of Meaning as a Layered Theory of Being
Marc Champagne
Kwantlen Polytechnic University
December 2015
Sign Systems Studies 43(4):523-552
DOI:10.12697/SSS.2015.43A10
https://www.researchgate.net/publication/310446520_A_Less_Simplistic_Metaphysics_Peirce%27s_Layered_Theory_of_Meaning_as_a_Layered_Theory_of_Being
VIRTUAL LOGIC–THE COMBINATORIAL HIERARCHY: ‘ONE, TWO, THREE, INFINITY!’
Author: Kauffman, Louis
Source: Cybernetics & Human Knowing, Volume 19, Number 3, 2012, pp. 83-91(9)
Publisher: Imprint Academic
https://www.ingentaconnect.com/content/imp/chk/2012/00000019/00000003/art00006
6.3 ONE, TWO, THREE … ETERNITY
Subchapter in book
Cyber Semiotics: Why Information is not enough
Soren Brier
Peirce’s Prepunctual Continuum
MATTHEW MOORE
CUADERNOS DE SISTEMÁTICA PEIRCEANA
Número 7 – 2015
CENTRO DE SISTEMÁTICA PEIRCEANA
CSP
Time and the Continuum. An Introduction to the Problem(s)
Marcello Garibbo
University of Siegen
Philosophy Kitchen #13 — Anno 7 — Settembre 2020 — ISSN: 2385-1945 — Il Tempo e il Continuo.
Is Synechism Necessary?
Matthew Moore
Cognitio, Sao Paulo, Vol 14, No 1, 2013
Continuity of Space and Theories of Intersections
from Euclid to Leibniz
Vincenzo De Risi
Brouwer and Weyl: The Phenomenology and mathematics of the intuitive continumm
M Van Atten; D Van Dalen; R Tieszen
Infinitesimals and the continuum
John L. Bell
A formalization of forcing and the unprovability of the continumm Hypothesis
Jesse Michael Han; Floris Van Doorn
Peirce’s Conception of Metaphysics
Joshua David Black
Phd Thesis 2017
Peirce’s Triadic Logic : Continuity, Modality, and L
Odland, Brent C.
MS Thesis, 2020
University of Calgary
on the structure of continua
G T Whyburn
Potential infinity and intuitiontic Logic
Oystein Linnebo, Stewart Shapiro and Geoffrey Hellman
Conceptions of the continuum
Solomon Feferman
2009
the continuum east and west
Peter G Jones
Philosophy Pathways, 185, May 2014
https://philarchive.org/archive/JONTCE
Cauchey’s Continuum
Karin Katz and Mikhail Katz
Dicisigns: Peirce’s Semiotic Doctrine of Propositions
Synthese, Vol 192, No 4, 2015
Real Numbers, Generalizations of the Reals, and Theories of Continua
Time and the continuum
Lambalgen and Pinosio
Indefinite Divisibility
Jeffrey Sanford Russell
Inconsistent Boundaries
Zach Weber and AJ Cotnoir
Peirce’s mathematical logical approach to discrete collections and the premonition of Continuity
Helio Rebello
Cantor, Peirce and the True Continuum
Peirce and Cantor on Continuity
Stephen Gardner
https://www.academia.edu/3721816/Peirce_and_Cantor_on_Continuity
Charles Peirce on the Continuity of Thought
Dinh Huyen My
BS Thesis 2021
Charles University
william James psychology and ontology of continuity
Michela Bella
Toward a clarity of the extreme value theorem
Karin Katz
Mikhail Katz
Taras Kudryk
Time, Modality and three valued logic in Peirce and Lukasiewicz
Jose Renato Salatiel
Continuity and Mathematical Ontology in Aristotle
Keren Wilson Shatalov
The classical Continuum without points
Geoffrey Hellman and Stewart Shapiro
what is Categorical Structuralism?
Geoffrey Hellman
euclid’s geometry is just in our mind, rather than describing the real world
Arturo Tozzi
James Peters
The logic of Kant’s Temporal Continuum
Riccardo Pinosio
Varieties of Logic
Stewart Shapiro
Philosophical Aspects of Peirce’s Trivalent Logic
Jose Renato Salatiel
Philosophical problem of relations according to Peirce: Alliances towards an ontology of relations regarding two aspects of Synechism
Helio Rebello Cardoso Jr
Thein Spinelli Farraz
Are points (Necessarily) unextended?
Philip Ehrlich
C. S. Peirce and Aristotle on Time
Demetra Sfendoni-Mentzou
Applied Communicology in Org PR and R&D: Peirce on Synechism, Fuller on Synergetics, Gordon on Synectics, and Alinsky on Socialism
Richard Lanigan
The Continuity Debate: Dedekind, Cantor, Du Bois-Reymond, and Peirce on Continuity and Infinitesimals
Alison Walsh, Benjamin Lee Buckley
Docent Press, 2012
‘Hermann Weyl on intuition and the continuum’.
Bell, John L. (2000).
Philosophia Mathematica 8 (3):259-273.
Click to access Hermann%20Weyl.pdf
A Primer of Infinitesimal Analysis.
Bell, John L. (1998).
Cambridge University Press.
The Continuum: A Critical Examination of the Foundations of Analysis
Weyl, Hermann,
Dover (1987)
Brouwer and Weyl: The Phenomenology and Mathematics of the Intuitive Continuumt
M. Atten, D. Dalen, R. Tieszen
Published 1 April 2001
Hermann Weyl’s intuitionistic mathematics.
D. van Dalen.
Bulletin of Symbolic Logic, 1:145–169, 1995.
Mystic, geometer, and intuitionist. The life of L.E.J. Brouwer.
1: The dawning revolution.
D. van Dalen.
Clarendon Press, Oxford, 1999.
The Continuity of Being: C.S. Peirce’s Philosophy of Synechism
by Brian Kemple
Epoché Philosophy Monthly
Issue #19 January 2019
https://epochemagazine.org/19/the-continuity-of-being-c-s-peirces-philosophy-of-synechism/
The Continuity of Peirce’s Thought
by Kelly A. Parker
Book 1998
The Concept of Continuity in Charles Peirce’s Synechism.
Benedict, George Allen (1973).
Dissertation, State University of New York at Buffalo
Peirce’s topical theory of continuity
Authors: Matthew E. Moore
April 2013 Synthese 192(4)
DOI:10.1007/s11229-013-0337-6
https://www.researchgate.net/publication/272036759_Peirce%27s_topical_theory_of_continuity
“Peirce’s logic of continuity: Existential graphs and non-Cantorian continuum.”
Fernando Zalamea.
Rev. Mod. Log. 9 (1-2) 115 – 162, November 2001 – November 2003.
Peirce’s Logic of Continuity: A Conceptual and Mathematical Approach
Fernando Zalamea
Book 2012
ISBN/EAN13: 0983700494 / 9780983700494
One, two, three . . . continuity: C.S. Peirce and the nature of the continuum
Author: Robertson, R.
Source: Cybernetics & Human Knowing, Volume 8, Numbers 1-2, 1 January 2001, pp. 7-24(18)
https://www.ingentaconnect.com/content/imp/chk/2001/00000008/f0020001/74?crawler=true
Does Continuity Allow For Emergence?
An Emergentist Reading Of Peirce’s Evolutionary Thought
Maria Regina Brioschi
https://doi.org/10.4000/ejpap.1647
https://journals.openedition.org/ejpap/1647
Peirce´s pragmatic meanings of mind and synechism
Lucia Santaella
Full professor-Graduate program in Communication and Semiotics São Paulo Catholic University; member of the Advisory Board of the Peirce Edition Project
https://www.pucsp.br/~lbraga/epap_peir4.htm
Feeling Our Way Forward: Continuity and Discontinuity Within the Cosmic Process,
Joseph A. Bracken S.J. (2010)
Theology and Science, 8:3, 319-331, DOI: 10.1080/14746700.2010.492625
Continuity and Inheritance: Kant’s Critique of Judgment and the Work of C.S. Peirce
John Kaag
Varieties of Synechism: Peirce and James on Mind–World Continuity.
Rosa M. Calcaterra;
The Journal of Speculative Philosophy 1 October 2011; 25 (4): 412–424. doi: https://doi.org/10.5325/jspecphil.25.4.0412
Peirce’s Philosophical Perspectives.
8 Peirce on Continuity
Potter, Vincent G.
New York: Fordham University Press, 2019., doi:10.1353/book.67375.
https://muse.jhu.edu/pub/93/oa_monograph/chapter/2379541
Diagrams, Visual Imagination, and Continuity in Peirce’s Philosophy of Mathematics
2023
THEORIES OF CONTINUITY AND INFINITESIMALS: FOUR PHILOSOPHERS OF THE NINETEENTH CENTURY
Lisa Keele
Doctor of Philosophy Thesis
in the Department of Philosophy,
Indiana University
May 2008
ProQuest Dissertations Publishing, 2008. 3319910.
TWO NEW GESTURES
ON PEIRCE’S CONTINUUM AND THE EXISTENTIAL GRAPHS
Fernando Zalamea (Universidad Nacional de Colombia)
77 Lebenswelt, 13 (2018)
Two New Gestures
on Peirce’s Continuum
and the Existential Graphs: Plurality of Pragmatic Imagination
Fernando Zalamea
Departamento de Matemáticas Universidad Nacional de Colombia
Associazione Pragma – 10th Anniversary Università degli Studi di Milano
October 18 2017
Click to access Milano(Ottobre2017).pdf
‘Logic of Relations and Diagrammatic Reasoning: Structuralist Elements in the Work of Charles Sanders Peirce’,
Carter, Jessica,
in Erich H. Reck, and Georg Schiemer (eds), The Prehistory of Mathematical Structuralism (New York, 2020; online edn, Oxford Academic, 18 June 2020), https://doi.org/10.1093/oso/9780190641221.003.0010, accessed 12 Apr. 2023.
https://academic.oup.com/book/41041/chapter/349349072
Peirce on continuity and his critique of Cantor and Dedekind.
Dauben, J. W. (1981).
In K. L. Ketner, J. M. Ransdell, C. Eisele, M. H. Fisch, and C. S. Hardwick (eds.), Graduate Studies Texas Tech University, pp. 93-98. Texas Tech Press.
The Peircean Continuum
Francisco Vargas
Matthew E. Moore
In book: The History of Continua (pp.328-346)
December 2020
DOI:10.1093/oso/9780198809647.003.0014
Advances in Peircean Mathematics
The Colombian School
Edited by: Fernando Zalamea
Volume 7 in the series Peirceana
https://doi.org/10.1515/9783110717631
https://www.degruyter.com/document/doi/10.1515/9783110717631/html
Charles Peirce and Modern Science
T L Short
Cambridge University Press
Online publication date: October 2022
Print publication year: 2022
Online ISBN: 9781009223508
DOI: https://doi.org/10.1017/9781009223508
Peirce’s Theory of Signs
T L Short
Publisher: Cambridge University Press
Online publication date: July 2009
Print publication year: 2007
Online ISBN: 9780511498350
DOI: https://doi.org/10.1017/CBO9780511498350
The Practical Peirce: An Introduction to the Triadic Continuum Implemented as a Computer Data Structure
Author John Zuchero
Publisher iUniverse, 2007
ISBN 0595441122, 9780595441129
The Triadic Continuum is the invention of Jane Mazzagatti, a mathematician and software engineer. Mazzagatti came upon the idea for this new computer data structure, which is based on the work of Charles Peirce, while working on a project for Unisys Corporation. This same structure has proven commercially valuable in the efficient way it stores and allows for the analysis of large datasets. However, while learning about the nature of the structure she discovered more far-reaching implications to areas other than computer science. Charles Peirce was fascinated with how the mind reasons and with all of the scientific and philosophical implications of the mechanisms of how the brain records experience, constructs memories, and accesses previously stored experience and knowledge. Mazzagatti believes that she has rediscovered the structure of the Triadic Continuum, which is the foundation of many of Peirce’s key theories dealing with human reasoning and the logic of thought.
In this book the author, who worked with Mazzagatti writing patents for the invention, explains how this structure is unlike any other computer data structure or type of Artificial Intelligence-but more importantly why this structure may very well be a model for human cognition.