Square and Circle of Hindu Temple Architecture
Source: Khajuraho Group of Monuments/Wikipedia
Khajuraho temples use the 8×8 (64) Vastupurusamandala Manduka grid layout plan (left) found in Hindu temples. Above the temple’s brahma padas is a Shikhara (Vimana or Spire) that rises symmetrically above the central core, typically in a circles and turning-squares concentric layering design (right) that flows from one to the other as it rises towards the sky.[31][46]
Key Terms
Temple in Man
- Panch Kosha Philosphy
- Triguna Philosophy
- Yoga Philosophy
- Seven Chakras
- Great Chain of Being
- Higher/Lower Levels
- Hierarchy Theory
- Ascent of Men
Temple of Men
- Beasts – Men – Devas – Gods
- Ratha in Architecture
- Triratha
- Panchratha
- Saptaratha
- Navratha
- Ayatan Plan Architecture
- Ekayatan
- Triayatan
- Panchayatan
- Saptayatan
- Chhadyashikhar
- Shikharanvit
- Valabhichhandaj
- Sandhar
- Prasad
- Nagara Architecture
- Odisha
- Chandella
- Solanki Maru Gurjara
- Mandapa in Architecture
- Ardh Mandapa
- Mandapa
- Maha Mandapa
- Vastu Purush Mandala
- Ceilings in Architecture
- Shikhar (Vimana, Spire)
- Temple and the Tank
- Temple and the Pond
- Temple and the River
- Temple and the Lake
- Square and Circle
- Earth and Heaven
- As Above, So Below
- As Below, So Above
- Amalaka
- Kalash
- Garbh Graha
- Outer to Inner
- Lower to Higher
- Purush Sukta
- Shri Sukta
- Antarala
- Pada Devta
- Lok Pals
- Dwar Pals
- Dik Pals
- Ayadi Calculations
- Toranas
- Vitana (Ceiling)
- Prakash and Vimarsh
- Terrestial to Celestial
Nagara (North Indian) Hindu Temple Architecture
Source: KHAJURAHO GROUP OF TEMPLES/Dr. Manoj Kumar

Source: KHAJURAHO GROUP OF TEMPLES/Dr. Manoj Kumar

Source: KHAJURAHO GROUP OF TEMPLES/Dr. Manoj Kumar

Source: KHAJURAHO GROUP OF TEMPLES/Dr. Manoj Kumar
Source: KHAJURAHO GROUP OF TEMPLES/Dr. Manoj Kumar

Source: KHAJURAHO GROUP OF TEMPLES/Dr. Manoj Kumar

Source: KHAJURAHO GROUP OF TEMPLES/Dr. Manoj Kumar

Source: TEMPLE ARCHITECTURE AND SCULPTURE

Source: Symbolism in Hindu Temple Architecture and Fractal Geometry – ‘Thought Behind Form’

Source: A Comparative Analysis of the Temples of Khajuraho and the Ruling Chandellas of India
Source: A Comparative Analysis of the Temples of Khajuraho and the Ruling Chandellas of India
Source: A Comparative Analysis of the Temples of Khajuraho and the Ruling Chandellas of India

Source: A Comparative Analysis of the Temples of Khajuraho and the Ruling Chandellas of India

Source: Lakshmana Temple, Khajuraho, Madya Pradesh, India
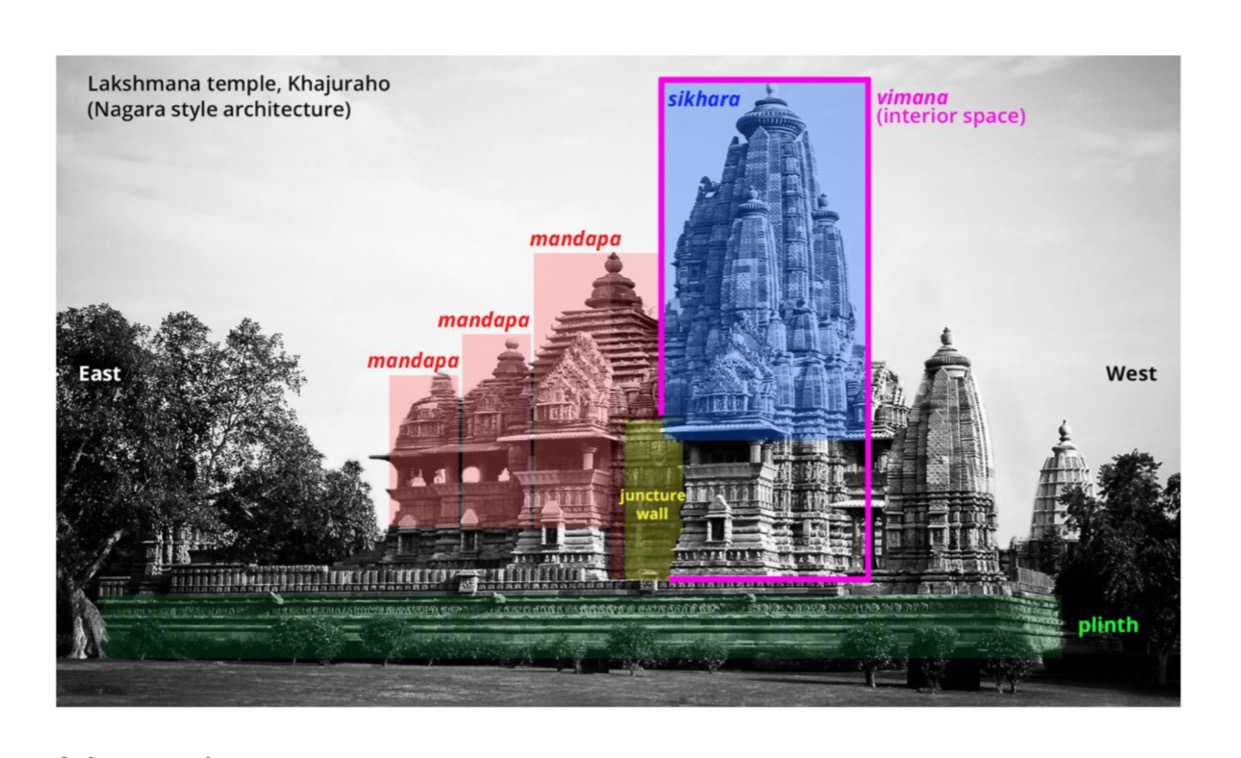
Source: Lakshmana Temple, Khajuraho, Madya Pradesh, India

Source: The Religious Imagery of Khajuraho

Source: The Religious Imagery of Khajuraho
Source: KHAJURAHO GROUP OF MONUMENTS / Group 12
Source: The Temples of Khajuraho in Central India

Ratha in Architecture
Source: https://en.wikipedia.org/wiki/Ratha_(architecture)

Square and Circle within a Temple
- Ground Plan (Square) and Ceiling (Circle)
- Using Circles to Generate Squares for Ground Plan
- Pillars with Square Base and Circular Top
Vastu Purusha Mandala
Source: Hindu temple architecture/Wikipedia

Source: Hindu temple architecture/Wikipedia
Source: Hindu temple architecture/Wikipedia

Source: Khajuraho Group of Monuments/Wikipedia
Architecture of the temples
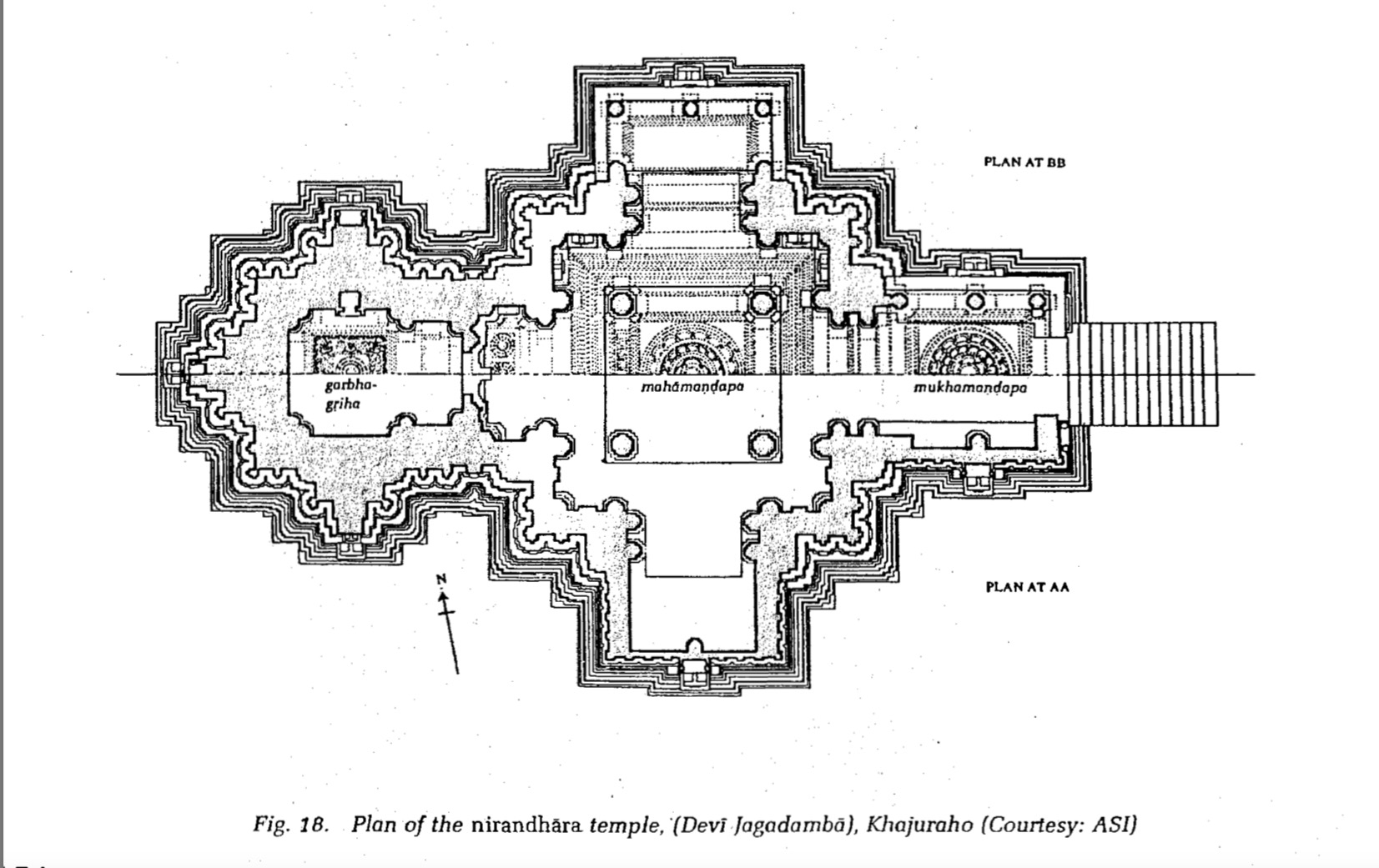
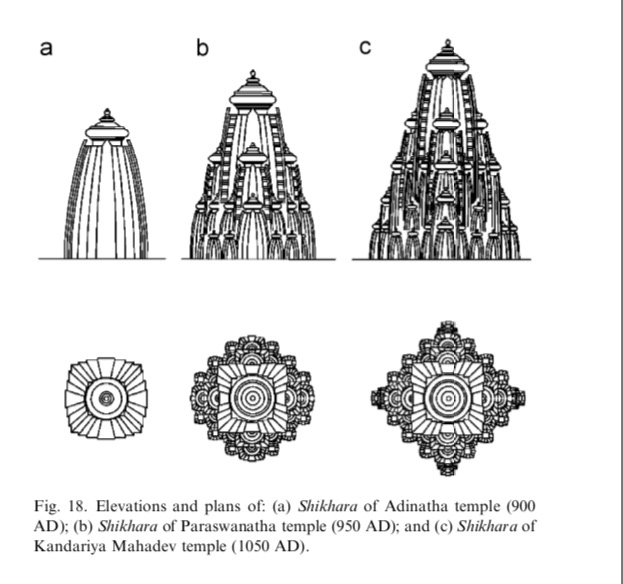
The layout plan of Kandariya Mahadeva Temple. It uses the 64 pada grid design. Smaller Khajuraho temples use the 9, 16, 36 or 49 grid mandala plan.[42]
Khajuraho temples, almost all Hindu temple designs, follow a grid geometrical design called vastu-purusha-mandala.[43] This design plan has three important components – Mandala means circle, Purusha is universal essence at the core of Hindu tradition, while Vastu means the dwelling structure.[44]
The design lays out a Hindu temple in a symmetrical, concentrically layered, self-repeating structure around the core of the temple called garbhagriya, where the abstract principle Purusha and the primary deity of the temple dwell. The shikhara, or spire, of the temple rises above the garbhagriya. This symmetry and structure in design is derived from central beliefs, myths, cardinality and mathematical principles.[45]
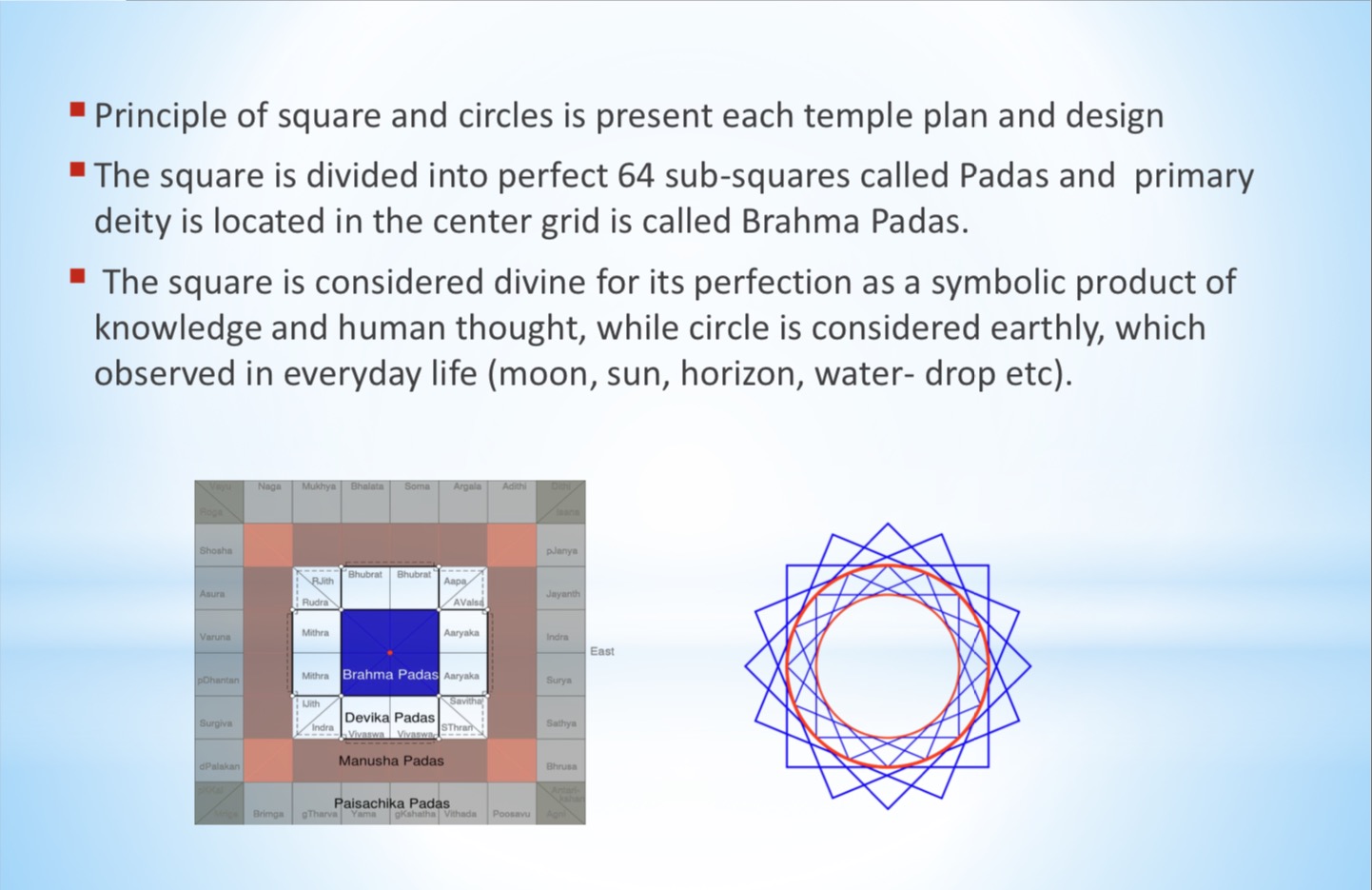
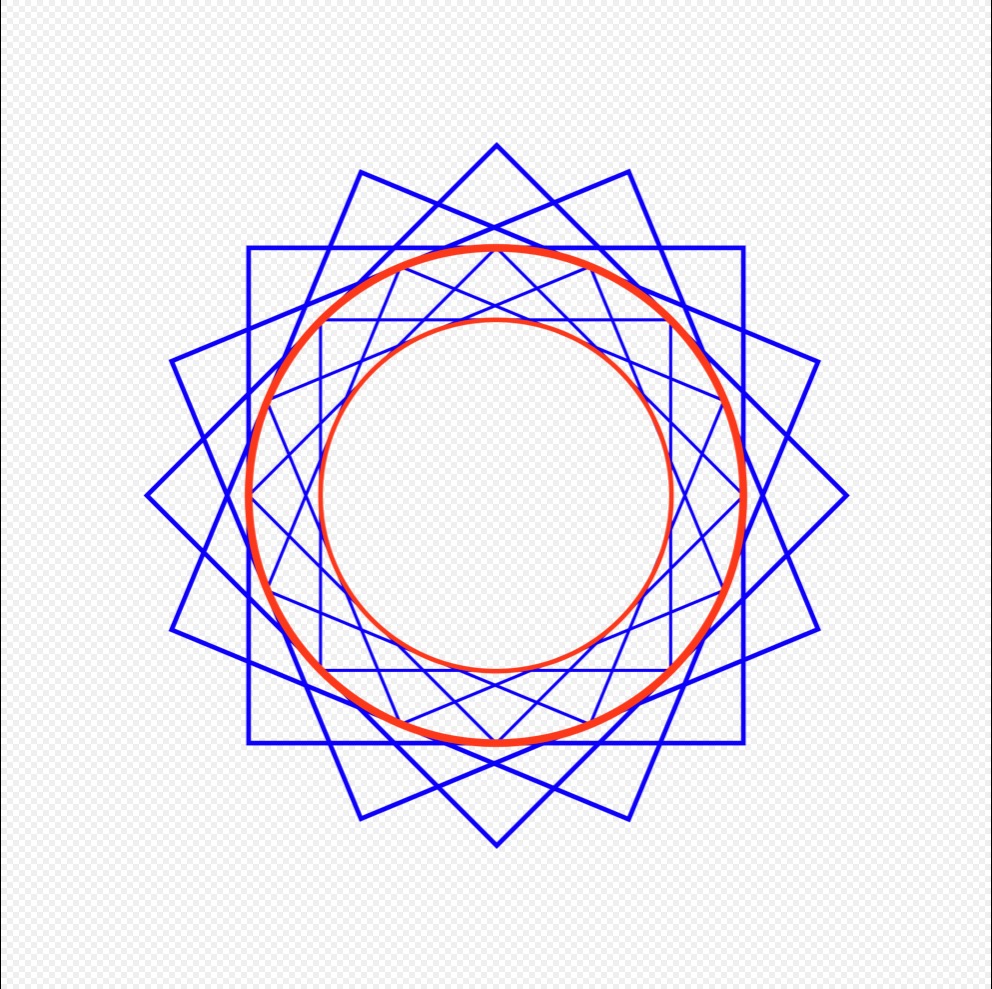
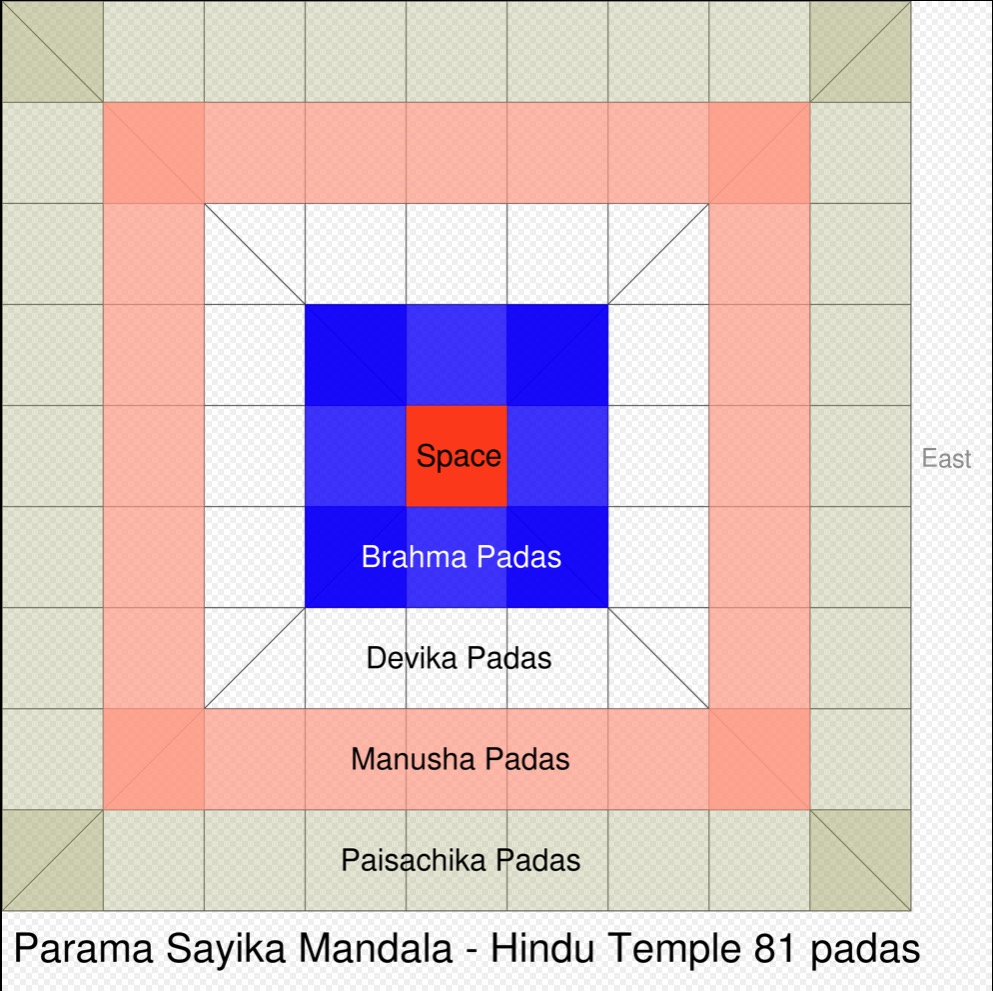
The circle of mandala circumscribe the square. The square is considered divine for its perfection and as a symbolic product of knowledge and human thought, while circle is considered earthly, human and observed in everyday life (moon, sun, horizon, water drop, rainbow). Each supports the other.[31] The square is divided into perfect 64 sub-squares called padas.[43]
Most Khajuraho temples deploy the 8×8 (64) padas grid Manduka Vastupurushamandala, with pitha mandala the square grid incorporated in the design of the spires.[42] The primary deity or lingas are located in the grid’s Brahma padas.
Khajuraho temples use the 8×8 (64) Vastupurusamandala Manduka grid layout plan (left) found in Hindu temples. Above the temple’s brahma padas is a Shikhara (Vimana or Spire) that rises symmetrically above the central core, typically in a circles and turning-squares concentric layering design (right) that flows from one to the other as it rises towards the sky.[31][46]
The architecture is symbolic and reflects the central Hindu beliefs through its form, structure, and arrangement of its parts.[47] The mandapas, as well as the arts, are arranged in the Khajuraho temples in a symmetric repeating patterns, even though each image or sculpture is distinctive in its own way. The relative placement of the images are not random but together they express ideas, just like connected words form sentences and paragraphs to compose ideas.[48] This fractal pattern that is common in Hindu temples.[49] Various statues and panels have inscriptions. Many of the inscriptions on the temple walls are poems with double meanings, something that the complex structure of Sanskrit allows in creative compositions.[29]
All Khajuraho temples, except one, face sunrise, and the entrance for the devotee is this east side.
An illustration of Khajuraho temple Spires (Shikhara, Vimana) built using concentric circle and rotating-squares principle. Four spires (left) are shown above, while the inside view of one Shikara ceiling (right) shows the symmetric layout.
Above the vastu-purusha-mandala of each temple is a superstructure with a dome called Shikhara (or Vimana, Spire).[44] Variations in spire design come from variation in degrees turned for the squares. The temple Shikhara, in some literature, is linked to mount Kailash or Meru, the mythical abode of the gods.[31]
In each temple, the central space typically is surrounded by an ambulatory for the pilgrim to walk around and ritually circumambulate the Purusa and the main deity.[31] The pillars, walls, and ceilings around the space, as well as outside have highly ornate carvings or images of the four just and necessary pursuits of life – kama, artha, dharma, and moksa. This clockwise walk around is called pradakshina.[44]
Larger Khajuraho temples also have pillared halls called mandapa. One near the entrance, on the east side, serves as the waiting room for pilgrims and devotees. The mandapas are also arranged by principles of symmetry, grids, and mathematical precision. This use of same underlying architectural principle is common in Hindu temples found all over India.[50] Each Khajuraho temple is distinctly carved yet also repeating the central common principles in almost all Hindu temples, one which Susan Lewandowski refers to as “an organism of repeating cells”.[51]
Source: PARAMETRIZING INDIAN KARNATA-DRAVIDA TEMPLE USING GEOMETRY
Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE
Layout of a Hindu temple pursues a geometrical design known as vastu-purusha-mandala, the name of which is derived from the three vital components of the design namely Vastu meaning Vaas or a place of dwelling; Purusha, meaning the Universal principle; and Mandala meaning circle. Vastupurushamandala is a mystical diagram referred in Sanskrit as a Yantra. The symmetrical and self-repeating model of a Hindu temple demonstrated in the design is derived from the primary convictions, traditions, myths, fundamentality and mathematical standards. According to Vastupurushamandala, the most sacred and typical template for a Hindu temple is the 8×8 (64) grid Manduka Hindu Temple Floor Plan also referred as Bhekapada and Ajira. The layout displays a vivid saffron centre with intersecting diagonals which according to Hindu philosophy symbolises the Purusha. The axis of the Mandir is created with the aid of the four fundamentally significant directions and thus, a perfect square is created around the axis within the available space. This square which is circumscribed by the Mandala circle and divided into perfect square grids is held sacred. On the other hand, the circle is regarded as human and worldly that can be perceived or noticed in daily life such as the Sun, Moon, rainbow, horizon or water drops. Both the square and the circle support each other. The model is usually seen in large temples while an 81 sub-square grid is observed in ceremonial temple superstructures. Each square within the main square referred as „Pada‟ symbolise a specific element that can be in the form of a deity, an apsara or a spirit. The primary or the innermost square/s of the 64 grid model called Brahma Padas is dedicated to Brahman. The Garbhagruha or centre of the house situated in the Brahma Padas houses the main deity. The outer concentric layer to Brahma Padas is the Devika Padas signifying facets of Devas or Gods which is again surrounded by the next layer, the Manusha Padas, with the ambulatory. The devotees circumambulate clockwise to perform Parikrama in the Manusha Padas with Devika Padas in the inner side and the Paishachika Padas, symbolising facets of Asuras and evils, on the outer side forming the last concentric square. The three outer Padas in larger temples generally adorn inspirational paintings, carvings and images with the wall reliefs and images of different temples depicting legends from different Hindu Epics and Vedic stories. Illustrations of artha, kama, dharma and moksha can be found in the embellished carvings and images adorning the walls, ceiling and pillars of the temples.
Source: A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE
Source: VASTU PURUSHA MANDALA- A HUMAN ECOLOGICAL FRAMEWORK FOR DESIGNING LIVING ENVIRONMENTS
Source: Space and Cosmology in the Hindu Temple

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho
According to Hindu philosophy, the main goal of man’s life is to achieve the ultimate liberation from the illusionary world where he suffers from his endless rebirth. Krishna says in Bhagavad Gita,9 if man worships, devotes and meditates to the manifested form of the wholeness of infinity, and sees the truth of its manifestation; he will surpass the confusion of the never-ending cycles of rebirth in this physical world, and finally will assimilate with the God. 10 Hindu calls it moksha.11 It brings the ultimate peace and harmony in man’s life. But how one, from the physical world, can practice to realize this ultimate truth of the creation? Brihatsamhita12 and Sthapatyaveda13 give the solution as the temple which should act as the microcosm of the cosmos [9]. It should be the bridge for the man of physical world to the God of divine world [10].
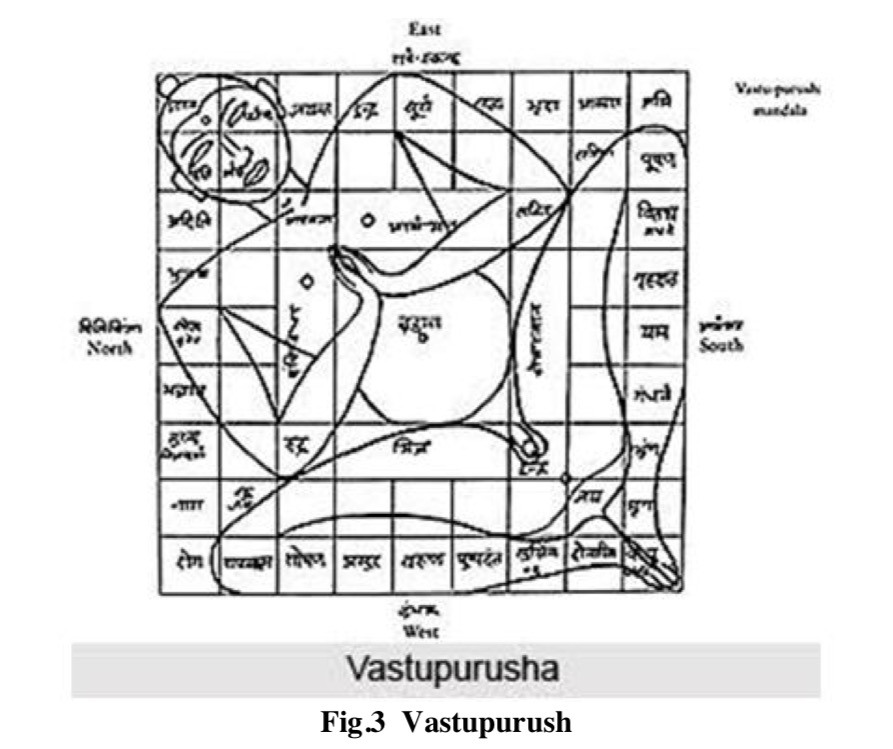
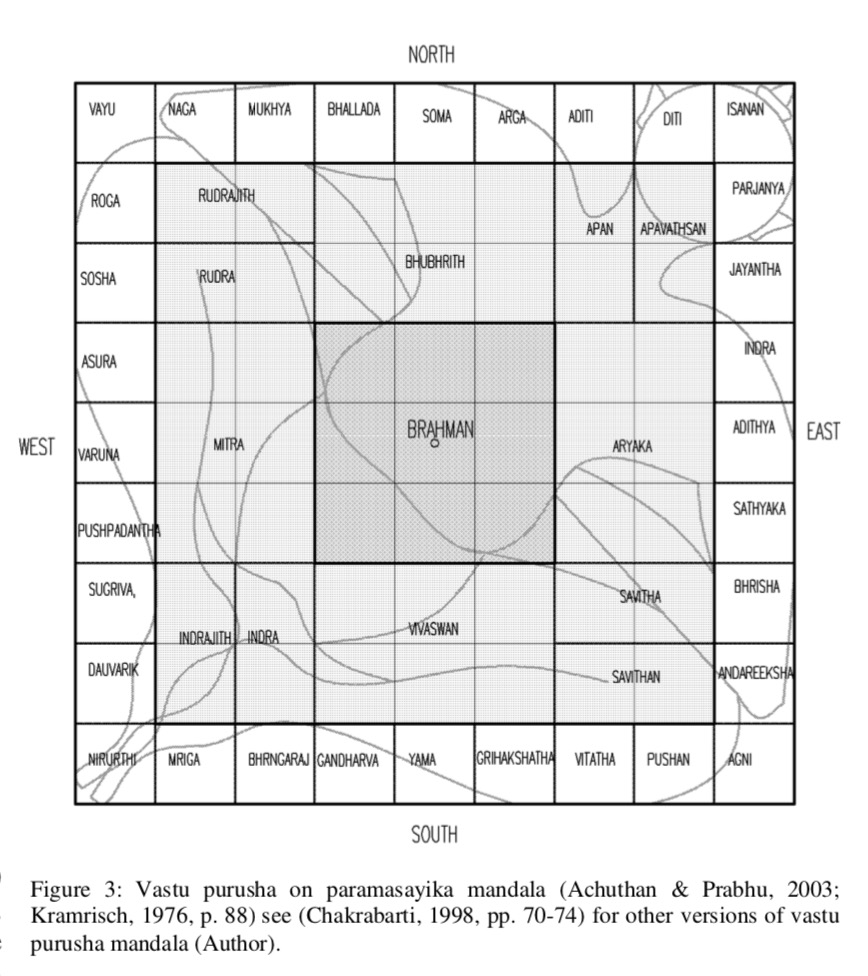
To connect the physical world with the divine world and to reflect the truth of creation, the layout of cosmos was copied graphically in the foundation of temple. Here, a mythical incident was interwoven where a formless being covered the sky and was, immediately, arrested down to the earth by the creator Brahma and other gods. This supernatural fact was depicted graphically by vastu purusha mandala, where vastu refers to physical environment, purusha refers to energy, power or cosmic being, and mandala is the diagram or chart. Central portion of the mandala represents the place of Brahma and other portions symbolize the other gods according to their capability. By laying down this metaphysical diagram in the foundation, various supernatural forces are captured beneath the temple whereas its centre is the source of cosmic energies. The basic shape of the vastu purusha mandala is a square which represents the earth [11]. Its four sides depict the four cardinal directions. It also symbolizes the order, the completeness of endless life and the perfectness of life and death [10]. According to Hindu philosophy, our mundane life is controlled by the number four—four castes, four stages of life, four great epochs or mahayugas, four heads of Brahma, the four Vedas etc. [12].
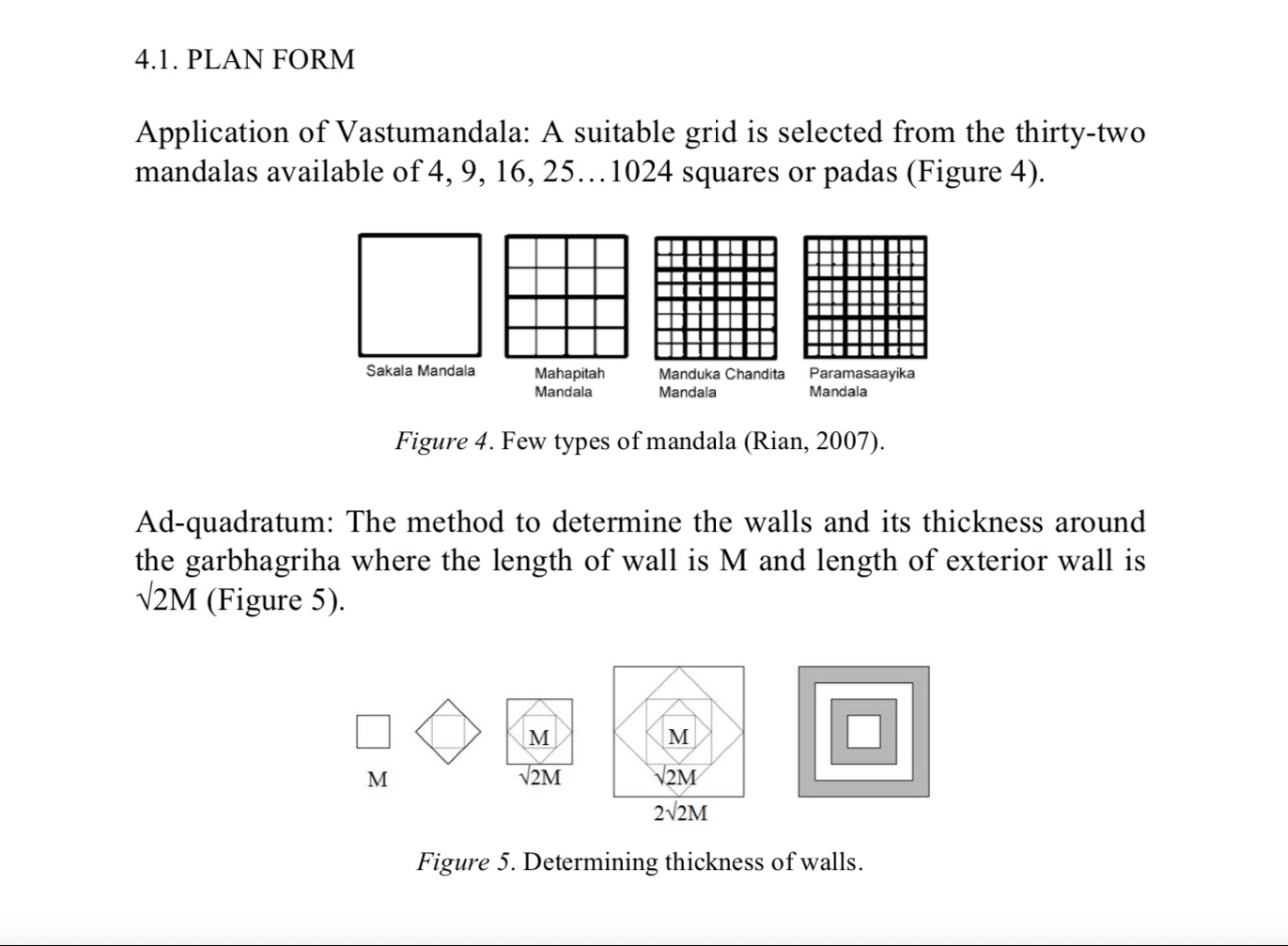
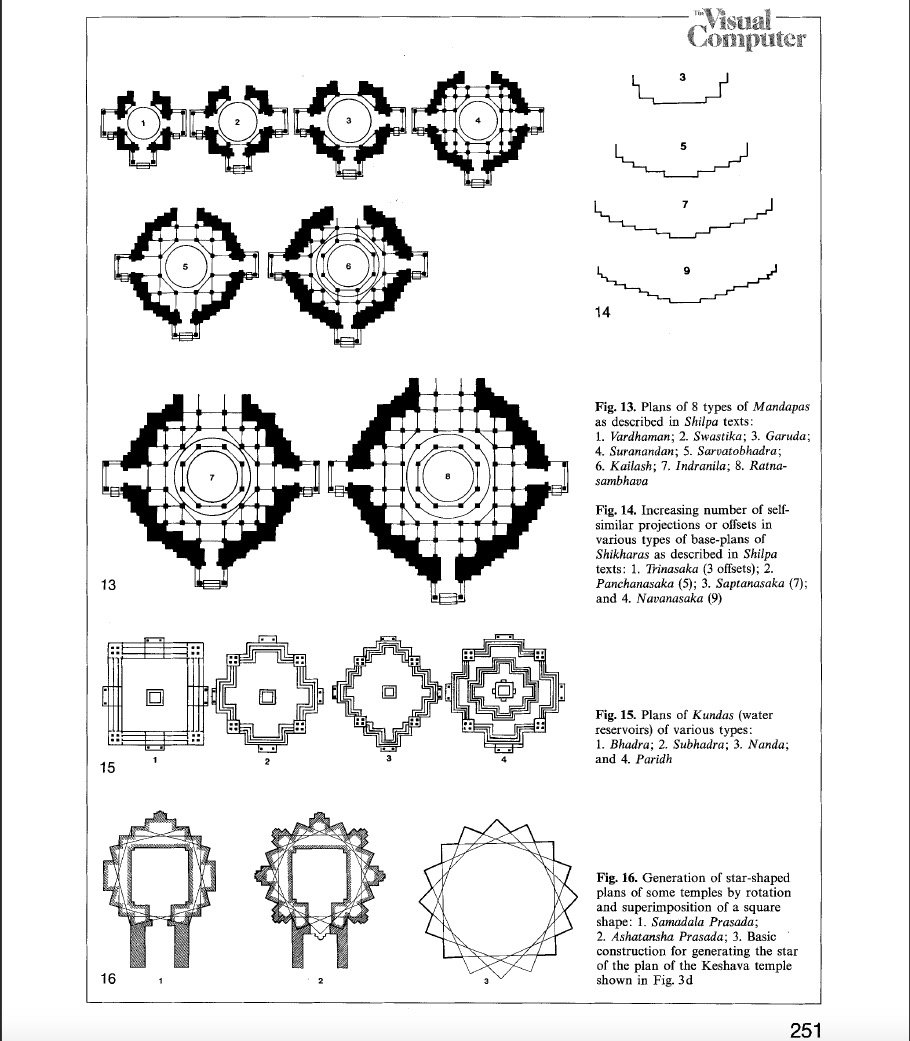
There are various types of vastu purusha mandala, which are nothing but the squares grids, produced from the basic shape; namely, a square which is known as sakala mandala. Each smaller square within the grid is called one pada. The number of pada may vary from 1, 4, 9, 16, 25 and so on 1024, where it follows the geometric progression of 1, 2, 3, 4, 5,…..,32 of common ratio 2. The mandala having even numbers of pada in its grid known as yugma squares mandala whereas the mandala, having odd numbers of pada known as ayugma squares mandala. Vastu purusha mandala is also known as different distinctive names according to the numbers of pada within the grid. The mandala having 1,4,9,16,25 and 36 numbers of pada within the grid are known as sakala mandala, pechaka mandala, pitah mandala, mahapitah mandala, manduka chandita mandala and para- masayika mandala, respectively14.
Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho

Source: Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho
Source: Maṇḍala in Architecture: Symbolism and Significance for Contemporary Design Education in India

Source: Maṇḍala in Architecture: Symbolism and Significance for Contemporary Design Education in India

Source: Revisiting the Vāstupuruṣamaṇḍala in Hindu Temples, and Its Meanings

Source: Revisiting the Vāstupuruṣamaṇḍala in Hindu Temples, and Its Meanings

Source: Revisiting the Vāstupuruṣamaṇḍala in Hindu Temples, and Its Meanings

Source: Revisiting the Vāstupuruṣamaṇḍala in Hindu Temples, and Its Meanings

Source: Role of Fractal Geometry in Indian Hindu Temple Architecture

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.
Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Source: HINDU TEMPLE: MODELS OF A FRACTAL UNIVERSE.

Types of Vastu Purush Mandala
Source: Indian Architectural Theory: Contemporary Uses of Vastu Vidya
- Sakala (1 x 1) = 1 Square
- Pechaka (2 x 2) = 4 Squares
- Pitha (3 x 3) = 9 Squares
- Mahapitha (4 x 4) = 16 Squares
- Upapitha (5 x 5) = 25 Squares
- Ugrapitha (6 x 6) = 36 Squares
- Sthandila (7 x 7) = 49 Squares
- Manduka (Chandita) (8 x 8) = 64 Squares
- Paramashayika (9 x 9) = 81 Squares
Types of Ceilings (Vitana) of Temples
Source: A Comparative Analysis of the Temples of Khajuraho and the Ruling Chandellas of India
- Samatala vitāna decorated with padmaśila
- Ksipta vitāna of Nābhicchanda order decorated with kola courses
- Ksipta vitāna of Nābhicchanda order decorated with gajatalu courses
- Ksipta vitāna of Nābhicchanda order in a set of diagonally arranged squares decorated with kola courses
- Ksipta vitāna of Nābhicchanda order in a set of nine arranged squares decorated with kola courses
- Ksipta vitāna of Nābhicchanda order in a set of eight circles intersected by a big circle in the center
- Sama-ksipta vitāna decorated with figural groups in the boxes
- Karotaka of Sabhmarga order
- Ksipta vitāna of Nābhicchanda order made of three diminishing squares decorated with kola courses
Questions on Relationships
(Kshetra)
- What is a relationship between the Temple and the Tank (Kunda)?
- What is a relationship between the Temple and the Pond (Talab)?
- What is a relationship between the Temple and the River (Nadi)?
- What is a relationship between the Temple and the Lake (Jheel)?
Square and Circle in a Group
Shiva temples (Squares) and Shakti Temples (Circular)
(Group of Squares and Group of Circles)
- Bateswer Group of Temples + Mitawali Chausath Yogini Temple (Circular)
- Khajuraho Group of Temples + Chausath Yogini Temple (Rectangular)
- Bhuvneswar Group of Temples + Hirapur Chausath Yogini Temple (Circular)
Temple Architecture Canonical Texts
Source: Rediscovering the Hindu Temple: The Sacred Architecture and Urbanism of India

My Related Posts
Fractal Geometry and Hindu Temple Architecture
Fractal and Multifractal Structures in Cosmology
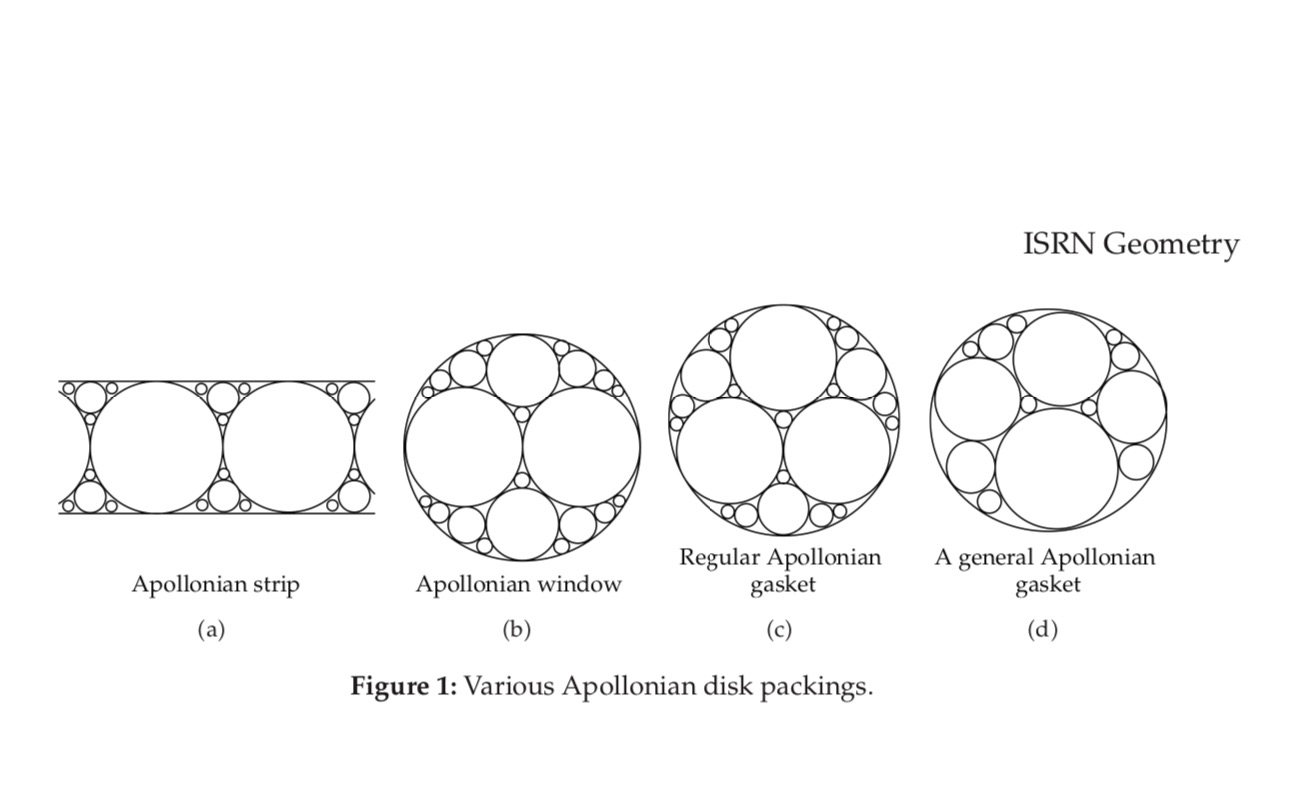
Indira’s Pearls: Apollonian Gasket, Circle and Sphere Packing
Chausath (64) Yogini Hindu Temples Architecture
Sapta Matrikas (Seven Mothers) and Cosmology
Key Sources of Research
Khajuraho Group of Monuments
UNESCO
https://whc.unesco.org/en/list/240/
Khajuraho Group of Monuments
WIKIPEDIA
https://en.wikipedia.org/wiki/Khajuraho_Group_of_Monuments
Maṇḍala and Practice in Nāgara Architecture in North India
Michael W. Meister
Journal of the American Oriental Society
Vol. 99, No. 2 (Apr. – Jun., 1979), pp. 204-219 (16 pages)
https://doi.org/10.2307/602657
https://www.jstor.org/stable/602657
https://www.academia.edu/783948/Mandala_and_Practice_in_Nagara_Architecture_in_North_India
Geometry and Measure in Indian Temple Plans: Rectangular Temples
Michael W. Meister
Artibus Asiae
Vol. 44, No. 4 (1983), pp. 266-296 (31 pages)
https://doi.org/10.2307/3249613
https://www.jstor.org/stable/3249613
https://www.academia.edu/783957/Geometry_and_measure_in_Indian_temple_plans_rectangular_temples
Measurement and proportion in Hindu temple architecture
Michael W Meister
1985, Interdisciplinary science reviews
https://www.academia.edu/783956/Measurement_and_proportion_in_Hindu_temple_architecture
The Hindu Temple, Vol 1
Stella Kramrisch,
Motilal Banarsidass, ISBN 978-81-208-0222-3
The Temples of Khajuraho in Central India
Krishna Deva
Ancient India, 15
ASI
Temple Architecture Khajuraho and Brihadeshwar
May 2022
Project: Indian Art and Architecture
Authors: Aparna Joshi
https://www.researchgate.net/publication/360928465_Temple_Architecture_Khajuraho_and_Brihadeshwar
KHAJURAHO GROUP OF TEMPLES
Dr. Manoj Kumar
Deptt Of AIHC & Archaeology
Indira Gandhi National Tribal University
KHAJURAHO
Based on the text of Krishna Deva
Published by
The Director General
ARCHAEOLOGICAL SURVEY OF INDIA New Delhi, 2002
.
A Comparative Analysis of the Temples of Khajuraho and the Ruling Chandellas of India
Chelsea Gill
May 2008
A Senior Thesis submitted in partial fulfillment of the requirements for the degree of Bachelor of Arts in Archaeological Studies University of Wisconsin-La Crosse
Homage to Khajuraho
Mulk Raj Anand
KHAJURAHO GROUP OF MONUMENTS
Group-12
MAHENDRA KUMAR (M23) RAHUL KUMAR GUPTA (M31) JAMUNA PRASAD BAHUGUNA (M21)
READING LOVE IMAGERY ON THE INDIAN TEMPLE
Vidya Dehejia
Click to access Dehejia-Reading-love-imagery-1998.pdf
Sculptural Representation on the Lakshmana Temple of Khajuraho in the Light of Prabodhachandrodaya
Devangana Desai
The Religious Imagery of Khajuraho
Devangana Desai
Click to access khajuraho_desai.pdf
Lakshmana Temple, Khajuraho, Madya Pradesh, India
Khajuraho Temples a Journey from Real to Surreal
By Dr Priyaankaa Mathur
April 7 2021
priyaankaamathur007@yahoo.co.in
ESAMSKRITI
https://www.esamskriti.com/a/Madhya-Pradesh/Kandariya-Mahadeva-Khajuraho.aspx
https://www.esamskriti.com/a/Madhya-Pradesh/Lakshmana-Temple-Khajuraho.aspx
https://www.esamskriti.com/e/Culture/India-Travel-Ad-Yatras/All-about-Khajuraho-Temples–1.aspx
KHAJURAHO – BREATHTAKING INSIGHT INTO TEMPLE ARCHITECTURE
·
ASPIRITBEDOUIN
Khajuraho photo essay
Dr. Uday Dokras
2021, Indo Nordic Author’s Collective
https://www.academia.edu/66939222/Khajuraho_photo_essay
Khajuraho In Perspective (Khajurāho in Perspective)
Kalyan Kumar Chakravarty
1994, Khajurāho in Perspective published by Commissioner, Archaeology and Museums, Madhya Pradesh
https://www.academia.edu/33809363/Khajuraho_In_Perspective_Khajurāho_in_Perspective_
Khajuraho Temples: symbolism of Sacred Union of the Divine – Feminine Energy & Masculine Consciousness
Medhavi Davda.
“Sacred space and symbolic form at Lakshmana Temple, Khajuraho (India),”
Dr. Cristin McKnight Sethi,
in Smarthistory, May 15, 2016, accessed March 10, 2023, https://smarthistory.org/lakshmana-temple/.
Investigating Architectural Patterns of Indian Traditional Hindu Temples through Visual Analysis Framework
March 2022
Aditya Kumar Singh
Maulana Azad National Institute of Technology, Bhopal
Vinay Mohan Das
Maulana Azad National Institute of Technology, Bhopal
Yogesh Kumar Garg
Maulana Azad National Institute of Technology, Bhopal
Mohammad Arif Kamal
King Fahd University of Petroleum and Minerals
Civil Engineering and Architecture 10(2):513-530
DOI:10.13189/cea.2022.100211
Maṇḍala in Architecture: Symbolism and Significance for Contemporary Design Education in India
Navin Piplani Ansal University India
Tejwant Singh Brar Ansal University India
IAFOR Journal of Education: Studies in Education
Volume 8 – Issue 4 – 2020
The Infinite Space
Manifestation of bindu and mandala in architecture
A thesis submitted in fulfilment of the requirements for the degree of Doctor of Philosophy
Jaffer Adam Ayub Khan
B.Arch (Madras)., M.Sc.Arch (Bartlett)., RIBA., RAIA
School of Architecture and Design College of Design and Social Context RMIT University
August 2017
HEAVEN ON EARTH
TEMPLES, RITUAL, AND COSMIC SYMBOLISM IN THE ANCIENT WORLD
edited by
DEENA RAGAVAN
with contributions by
Claus Ambos, John Baines, Gary Beckman, Matthew Canepa, Davíd Carrasco, Elizabeth Frood, Uri Gabbay, Susanne Görke, Ömür Harmanşah, Julia A. B. Hegewald, Clemente Marconi, Michael W. Meister, Tracy Miller, Richard Neer, Deena Ragavan, Betsey A. Robinson, Yorke M. Rowan, and Karl Taube
Papers from the Oriental Institute Seminar Heaven on Earth
Held at the Oriental Institute of the University of Chicago 2–3 March 2012
oi.uchicago.edu
Revisiting the Vāstupuruṣamaṇḍala in Hindu Temples, and Its Meanings
Young Jae Kim
Ph.D. in Architectural History and Theory (University of Pennsylvania, USA)
http://dx.doi.org/10.5659/AIKAR.2014.16.2.45
Research – Application of Bindu and Mandala as a model for Cultural and Sacred Architecture
Jaffer Khan
May 27, 2017
Listen how the wise one begins construction of a house for Visnu: Chapters 1-14 of the Hayasirsa Pancaratra
Raddock, Elisabeth Eva
2011
https://escholarship.org/uc/item/83r393vc
Click to access qt83r393vc.pdf
Evolution and Interconnection: Geometry in Early Temple Architecture
Author : Sambit Datta
Published in: Digital Techniques for Heritage Presentation and Preservation
INFINITE SEQUENCES IN THE CONSTRUCTIVE GEOMETRY OF 10TH CENTURY HINDU TEMPLE SUPERSTRUCTURES
Dr. Sambit Datta
Senior Lecturer, Deakin University sdatta@deakin.edu.au
https://espace.curtin.edu.au/bitstream/handle/20.500.11937/26171/202269_202269.pdf?sequence=2
On the Idea of the Mandala as a Governing Device in Indian Architectural Tradition
Sonit Bafna
Georgia Institute of Technology
March 2000
The Journal of the Society of Architectural Historians 59(1):26-49
DOI:10.2307/991561
Orissan Temple Architecture and Vastu Purusha Mandala for evolution process
December 2012
Partha Sarathi Mishra
Sri Sri University
Shape and Geometry of Orissa Temple Architecture
Partha Sarathi Mishra
IIT Roorkee M Tech Thesis
2012
http://shodhbhagirathi.iitr.ac.in:8081/jspui/handle/123456789/2017?mode=full
Wikipedia Pages on
https://en.wikipedia.org/wiki/Hindu_temple
https://en.wikipedia.org/wiki/Hindu_temple_architecture
https://en.wikipedia.org/wiki/Temple_tank
https://en.wikipedia.org/wiki/Ratha_(architecture)
https://en.wikipedia.org/wiki/Panchayatana_(temple)
https://en.wikipedia.org/wiki/Mandapa
https://en.wikipedia.org/wiki/Ardhamandapa
Temple Architecture-Devalaya Vastu –Part One (1 of 9)
sreenivasarao’s blogs
“Naturalizing Buddhist Cosmology in the Temple Architecture of China: The Case of the Yicihui Pillar.”
Tracy Miller
In Heaven on Earth: Temples, Ritual, and Cosmic Symbolism in the Ancient World
(The University of Chicago Oriental Institute Seminars, No. 9), edited by Deena Ragavan, 17-39. Chicago: University of Chicago Oriental Institute, 2013.
“Of Palaces and Pagodas: Palatial Symbolism in the Buddhist Architecture of Early Medieval China.”
Tracy Miller
Frontiers of History in China 10.2 (2015): 222-263.
Seeds and Mountains: The Cosmogony of Temples in South Asia
Michael W Meister
2013, HEAVEN ON EARTH TEMPLES, RITUAL, AND COSMIC SYMBOLISM IN THE ANCIENT WORLD
https://www.academia.edu/3658884/Seeds_and_Mountains_The_Cosmogony_of_Temples_in_South_Asia
Role of Fractal Geometry in Indian Hindu Temple Architecture
Dhrubajyoti Sardar
M.Arch Scholar
Architecture & Planning Department, IIT Roorkee
Roorkee, Uttarakhand, India
S. Y. Kulkarni
Professor & Former Head Architecture & Planning Department, IIT Roorkee Roorkee, Uttarakhand, India
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181 Vol. 4 Issue 05, May-2015
https://www.academia.edu/43863568/IJERT_Role_of_Fractal_Geometry_in_Indian_Hindu_Temple_Architecture
Physical Fractals: Self Similarity and Square-Integratibility
Akhlesh Lakhtakia
Penn State
Speculations in Science and Technology 18, 153-156, 1995
Dancing Architecture: The parallel evolution of Bharatanātyam and South Indian Architecture
Kavitha Jayakrishnan
University of Waterloo
Master of Architecture Thesis 2011
https://uwspace.uwaterloo.ca/bitstream/handle/10012/6356/Jayakrishnan_Kavitha.pdf?sequence=1
https://uwspace.uwaterloo.ca/handle/10012/6356?show=full
Building Science of Indian Temple Architecture
Shweta Vardia
shwetavardia@gmail.com
2008 MS Thesis
Universidade do Minho, Portugal
Shapes, Patterns and Meanings in Indian Temple Architecture
Tanisha Dutta*, V. S. Adane
Department of Architecture and Planning, Visvesvaraya National Institute of Technology Nagpur, India *Corresponding author: ar.tanisha.dd@gmail.com
Received July 17, 2018; Revised August 20, 2018; Accepted November 05, 2018
American Journal of Civil Engineering and Architecture, 2018, Vol. 6, No. 5, 206-215
Available online at http://pubs.sciepub.com/ajcea/6/5/6 ©Science and Education Publishing DOI:10.12691/ajcea-6-5-6
Click to access ajcea-6-5-6.pdf
Hindu Temple: Models of a Fractal Universe.
Trivedi, K. (1993).
International Seminar on Mayonic Science and Technology,
243-258.
The Visual Computer 5, 243–258 (1989). https://doi.org/10.1007/BF02153753
https://link.springer.com/article/10.1007/BF02153753#citeas
Click to access Hindu_Temple_Models.pdf
Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho
IasefMd Riana Jin-HoParka HyungUk Ahna DongkukChangb
aDepartment of Architecture, Inha University, South Korea
bDepartment of Architecture, Chosun University, South Korea
Received 4 May 2006, Revised 21 July 2006, Accepted 15 January 2007, Available online 23 April 2007.
Building and Environment
Volume 42, Issue 12, December 2007, Pages 4093-4107
https://www.sciencedirect.com/science/article/abs/pii/S0360132307000273
Symbolism in Hindu Temple
Architecture through Fractal Geoemtry- ‘Thought Behind Form’.
Dutta, T., & V.S.Adane. (2014).
International Journal of Science and Research (IJSR), 489-497.
Temples of Odisha- the Geometry of Plan Form
Rinku Parashar
Assistant Professor Department of Architecture Engineering NIT, Raipur, 492010, India
Dr Abir Bandyopadhyay
Professor & Head Department of Architecture Engineering NIT, Raipur, 492010, India
IJIRST –International Journal for Innovative Research in Science & Technology| Volume 2 | Issue 10 | March 2016 ISSN (online): 2349-6010
Click to access IJIRSTV2I10036.pdf
Shape and geometrical study of fractal cosmology through Orissan Temple architecture
Partha Sarathi Mishra
january 2013
“Investigating Architectural Patterns of Indian Traditional Hindu Temples through Visual Analysis Framework,”
Aditya Kumar Singh, Vinay Mohan Das, Yogesh Kumar Garg, Mohammad Arif Kamal ,
Civil Engineering and Architecture, Vol. 10, No. 2, pp. 513-530, 2022.
DOI: 10.13189/cea.2022.100211.
“Infinite Sequences in the Constructive Geometry Of Tenth-Century Hindu Temple Superstructures”,
Datta, S.,
School of Architecture and Building Deakin University 1, Gheringhap Street Geelong VIC 3219 AUSTRALIA
sdatta@deakin.edu.au
Nexus Network Journal – Vol.12, No. 3, 2010 471 – 483
DOI 10.1007/s00004-010-0038-0; published online 15 September 2010
Kim Williams Books, Turin
https://link.springer.com/article/10.1007/s00004-010-0038-0
Evolution and Interconnection: Geometry in Early Temple Architecture
- S. Datta
- Published 2021
DOI:10.1007/978-3-030-57907-4_11
Corpus ID: 238053244
PARAMETRIZING INDIAN KARNATA-DRAVIDA TEMPLE USING GEOMETRY
SRUSHTI GOUD
BMS School of Architecture, Yelahanka, Bangalore, India
goudsrushti@gmail.com
Click to access ascaad2016_042.pdf
A REVIEW STUDY ON ARCHITECTURE OF HINDU TEMPLE
PRATHAMESH GURME1,PROF. UDAY PATIL2
1UG SCHOLAR,2HEAD OF DEPARTMENT, DEPARTMENT OF CIVIL ENGINEERING BHARATI VIDHYAPEETH’S COLLEGE OF ENGINEERING , LAVALE , PUNE , INDIA
INTERNATIONAL JOURNAL FOR RESEARCH & DEVELOPMENT IN TECHNOLOGY
The Dual Language of Geometry in Gothic Architecture: The Symbolic Message of Euclidian Geometry versus the Visual Dialogue of Fractal Geometry
Nelly Shafik Ramzy
Sinai University
Peregrinations: Journal of Medieval Art and Architecture
Volume 5 Issue 2 2015
SHAPE AND GEOMETRY OF ORISSAN TEMPLE ARCHITECTURE
Authors: Mishra, Partha Sarathi
MS Thesis, IITR 2012
http://localhost:8081/xmlui/handle/123456789/2017
http://shodhbhagirathi.iitr.ac.in:8081/jspui/handle/123456789/2017
Vastu Purusha Mandala – A human ecological framework for designing living environments.
Venugopal, Jayadevi
In Jetty, C, Chandra, B, Bhashyam, A, & Prabhakara, R (Eds.) Proceedings of International Conference on Advances in Architecture and Civil Engineering (AARCV 2012), Volume 2.
Bonfring, India, pp. 870-877.
Rediscovering the Hindu Temple:
The Sacred Architecture and Urbanism of India
Vinayak Bharne and Krupali Krusche
Book, ISBN (10): 1-4438-4137-4, ISBN (13): 978-1-4438-4137-5
TEMPLE ARCHITECTURE AND SCULPTURE
NCERT
Space and Cosmology in the Hindu Temple
Subhash Kak
Presented at Vaastu Kaushal: International Symposium on Science and Technology in Ancient Indian Monuments, New Delhi, November 16-17, 2002.
Gender and space in temple architecture
D. Midhila
midhilachandra@gmail.com
Hindustan Institute of Technology and Sciences, Vijayawada, Andhra Pradesh
Dr. R. V. Nagarajan
rvnagarajan@hindustanuniv.ac.in
Hindustan Institute of Technology and Sciences, Padur, Chennai, Tamilnadu
International Journal of Advance Research, Ideas and Innovations in Technology
2020
The Role of Five Elements of Nature In Temple Architecture
Ar. Snigdha Chaudhary
International Journal of Scientific & Engineering Research Volume 8, Issue 7, July-2017 1149 ISSN 2229-5518
Trends in Fractal Dimension in Laxman and Kandariya Mahadev Temples, Khajuraho
Tanisha Dutta1,* and Vinayak S. Adane2
1Phd Research Scholar, Department of Architecture and Planning, Visvesvaraya National Institute of Technology, Nagpur- 440010, India.
2Professor, Department of Architecture and Planning, Visvesvaraya National Institute of Technology, Nagpur- 440010, India. (*Corresponding author)
nternational Journal of Applied Engineering Research ISSN 0973-4562 Volume 13, Number 3 (2018) pp. 1728-1741
© Research India Publications. http://www.ripublication.com
Hindu Temple Fractals
William J Jackson
https://www.academia.edu/347639/Hindu_Temple_Fractals
Indian Architectural Theory: Contemporary Uses of Vastu Vidya
Vibhuti Chakrabarti
Oxford University Press (1999)
ISBN 0195650417
Pancha Kosha Theory of Personality
Biswajit Satpathy
Sambalpur University
July 2018
The International Journal of Indian Psychology 6(2)
DOI:10.25215/0602.105
https://www.researchgate.net/publication/326258350_Pancha_Kosha_Theory_of_Personality
CRITICAL ANALYSIS OF PANCHAKOSHA THEORY OF YOGA PHILOSOPHY
Yagyik Mishra
SGT University
January 2019
World Journal of Pharmaceutical Research 8(13):413
DOI:10.20959/wjpr201913-16152
THE LEVELS OF HUMAN CONSCIOUSNESS AND CREATIVE FUNCTIONING: INSIGHTS FROM THE THEORY OF PANCHA KOSHA (FIVE SHEATHS OF CONSCIOUSNESS)
Maharaj K. Raina, Ph.D.
Woodland, CA
The Journal of Transpersonal Psychology, 2016, Vol. 48, No. 2
Panchakosha
Shiv Jakhar
International Journal of Yogic, Human Movement and Sports Sciences 2019; 4(1): 1382-1384
NURTURING THE WHOLE BEING: AN INDIAN PERSPECTIVE
PANCHA KOSHA VIVEKA PRAKARANAM
(Discrimination of the Five Sheaths)
PANCHADASI Chapter 3
Development of Panch Kosha
Human Resource Management
Indian Perspectives on Human Quality Development
Pathashala, MHRD, INDIA
Click to access 1513923600M6Q1DevelopmentofPanchkosha.pdf
The Pancha Koshas: Keys To Unveil Our True Self.
Aiswarya. H. N & Sowmya C. Nair
International Ayurvedic Medical Journal {online} 2019 {cited November, 2019}
Available from: http://www.iamj.in/posts/images/upload/2095_2100.pdf
PANCHA KOSHA VIVEKA
“Differentiation of the Five Sheaths”
PANCHADASHEE – 03
Composed by Sri Swami Vidyaranyaji
Reflections
by SWAMI GURUBHAKTANANDA
on the 32 Lectures delivered by Swami Advayanandaji, Acharya at the Chinmaya International Foundation, Veliyanad, Kerala. from April 28th 2017 – November 7th, 2017
Unit-5 Concept of Pancha Koshas, Concept of Panchmahabhutas
Issue Date: 2020
Publisher: Indira Gandhi National Open University, New Delhi
URI: http://egyankosh.ac.in//handle/123456789/59786
Appears in Collections: Block-2 Yogic Concepts of Health
https://egyankosh.ac.in/handle/123456789/59786
COMMENTARY ON THE PANCHADASI
SWAMI KRISHNANANDA
The Divine Life Society Sivananda Ashram, Rishikesh, India
Website: swami-krishnananda.org
“Vastu Purusha Mandala”,
Vini Nathan,
Nexus Network Journal, vol. 4, no. 3 (Summer 2002),
http://www.nexusjournal.com/N2002-Nathan.html
Hindu Temple and the Structure of Human Body
Sanskriti
Vastu-Vaastu
https://en.sthapatyaveda.net/vastuvaastu
Vaastu Purusha Mandalam
by Dr. V. Ganapati Sthapati
Book
Ayadi Calculations
by Dr. V. Ganapati Sthapati
Book
The Hindu Temple: An Introduction to its Meaning and Forms.
Michell, G. (1977, 1988).
Chicago, London: University of Chicago Press.
The temple architecture of india .
Hardy, A. (2007).
England: John Wiley & Sons Ltd.
Encyclopaedia of Indian temple architecture, South India, Lower Drāviḍadēśa 200 BC – AD 1324.
Meister M. W. (Ed.) (1999).
American Institute of Indian Studies and Manohar Publishers & Distributors. ISBN 81-7304-298-5.
Canonical Texts
The oldest and most complete canonical group of ancient texts includes
- Mayamata
- Mānasāra
- Samarāṇgana Sūtradhāra
- Rajavallabha
- Vishvakarma Praksha
Architecture of Mānasāra.
Acharya, P. K. (2010).
New Bharatiya Book Corporation. ISBN 978-81-8315-133-7.
Architecture of Mānasāra: illustrations of architectural and sculptural objects.
Acharya P. K. (2010).
New Bharatiya Book Corporation.
Samarāṅgaṇa Sūtradharā of Bhojadeva: an ancient treatise on architecture.
Sharma, S. K. (2012).
Parimal Publications. ISBN 978-81-7110-302-7.
The square and the circle of the Indian arts.
Vatsyayan, K. (1997).
Abhinav Publications.
Vastu-Purusha mandala.
Vatsyayan, K. (1986).
In C. Kagan (Ed.), Vistāra – The architecture of India, catalogue of the exhibition, The Festival of India. https://architexturez.net/doc/az-cf-123753
Indian temple architecture: Form and transformation.
Hardy, A. (1995).
Indira Gandhi National Centre for the Arts and Abhinav Publications.
ISBN 81-7017-312-4
Mayamatam: the treatise of housing, architecture and iconography.
Dagen, B. (1994).
Indira Gandhi National Centre for the Arts. ISBN: 81-208-1226-3.
Indian architectural theory and practice: Contemporary uses of Vastu Vidya
Chakrabarti, V. (1998).
Curzon. ISBN: 0-7007-1113-9.
VASTU SHASTRA PRINCIPLES APPLIED IN TEMPLE COMPLEX OF NEPAL
Ms. TABASSUM SIDDIQUI Assistant Professor
Kantipur International College, Kathmandu, Nepal
International Journal For Technological Research In Engineering
Volume 8, Issue 3, November-2020
Cosmologies of India
John McKim Malville
University of Colorado Boulder
August 2014
DOI:10.1007/978-94-007-3934-5_9717-2
In book: Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures (pp.1-16)
https://www.researchgate.net/publication/304183079_Cosmologies_of_India
Indian Temple Architecture, 3 Vols
Ananya Gandotra, 2011
An Encyclopedia of Hindu Architecture
Vol VII
Prasanna Kumar Acharya
Manasara Series, Volume I to VII
1946, Oxford Univ. Press
Shiva’s Waterfront Temples Reimaging the Sacred Architecture of India’s Deccan Region
Subhasini Kaligotla
PHD Thesis
Columbia University, 2015
”Indian Temple Architecture: form and Spaces”
Acharya,V.A,
Research Paper, Department of Architecture & Planning, I.I.T .Roorkee, Roorkee, India, 1991.
Understanding the Architecture of Hindu Temple: A Philosophical Interpretation
A. Bandyopadhyay
IJAEE, Vol 13, No 12, 2019
Temple Architecture
A Brief Overview and Its Symbolism
Purushottama Bilimoria
Temple Architecture and its Symbolism
Hindu Temple – A Systematic Study
Dr B Suresha
JETIR, December 2022, Vol 9, Issue 12
Significance of Mathematics and Geometry – Formation of Temples in India: The golden Era of Evolution
Santoshi Mishra and Sirisha David
ijeru, 2021, 01, 01, 050-055
The Iconography of Hindu Temple: Idea and Image
Sunil Kumar Patnaik
Transcendence from the matter to the mind
Understanding Spatial Experiance of a Temple Through its Architecture
Thesis, 2018 – 2019
Sneha B Krishnan
Ansal University, India
Maṇḍala in Architecture: Symbolism and Significance for Contemporary Design Education in India
Navin Piplani Ansal University India
Tejwant Singh Brar Ansal University India
IAFOR Journal of Education: Studies in Education
Volume 8 – Issue 4 – 2020
Mandapa: Its Proportion as a tool in Understanding Indian Temple Architecture
Ragima N Ramachandran
International Journal of Scientific & Engineering Research Volume 10, Issue 7, July-2019 2104 ISSN 2229-5518