Dasa (Ten) Maha Vidyas
Source: The Dasa Mahavidyas/Chamunda Swami ji
काली तारा महाविद्या षोडशी भुवनेश्वरी।
भैरवी छिन्नमस्ता च विद्या धूमावती तथा।
बगला सिद्ध विद्या च मातंगी कमलात्मिका
एता दशमहाविद्याः सिद्धविद्या प्रकीर्तिताः॥Kali Tara Mahavidya Shorashi Bhuvaneshwari
Bhairavi Chinnamasta cha Vidya Dhumavati Tatha
Vagala Sidhdhavidya cha Matangi Kamalatmika
Iti Das Mahavidya Sidhdhavidya Prakirtita



Source: Dus Mahavidyas

Key Terms
- Kali Maa
- Durga
- Parvati
- Parvati – Durga – Kali
- 8 – 16 – 64
- Shiva – Rudra – Bhairav
- 10 – 18 – 64
- Expansion of Series
- Sun, Moon, and Earth
- Series to Chamunda
- Series to Kali
- Kali Kul
- Sri Kul
- Dasa Avatars of Vishnu
- Dasa Maha Vidyas
- Aspects of Maa Kali
- Bhadra Kali
- Great Knowledge
- Wisdom Goddesses
- Terrible and Beautiful
- Evolution of Soul
- Evolution of Nature
- Angry and Peaceful
- Shakti
- Shaktism
- Tantra Science
- Mothers
- Dik Pals
- Ten Directions
- 9 Planets
- Sri Vidya
Ten Maha Vidyas
The 10 Mahavidyas are usually named in the following sequence:
- Kali
- Tara
- Tripura Sundari
- Bhuvaneshvari
- Bhairavi
- Chhinnamasta
- Dhumavati
- Bagalamukhi
- Matangi
- Kamala
Source: The Ten Great Cosmic Powers (Dasa Mahavidyas)
Chapter 1 Disciplines of Knowledge
He had studied the Vedas. Like all vaidiks of his time he took to priesthood and was eking out a living. Driven by poverty he approached someone to teach him a Mantra for getting rich quickly. Having got the Mantra, he took his seat in the front courtyard of his house and began practicing the repetition of the Mantra. Two hours would have passed and the Vaidik saw a beggar woman at attempt to drive her away as he did not want his japa to be interrupted by some words spoken in between. The beggar woman who was in tatters stooped down, patiently untied the knots of a bundle of rags, took out the small coins kept there and before the Vaidik knew what she was doing, threw the coins at his feet. The Vaidik naturally was taken aback and began to remonstrate. “Why, you have been asking for this for the past two hours” said she and went her way. The Vaidik stopped repeating his Mantra in sheer disgust and vowed that never again would he go after such pursuits.
This incident which happened years ago is quoted here for the flood of light it throws on certain basic principles of Tantra Shastra. Evidently, the man contacted with the help of the formula given to him an entity or a spirit, a low class of deity which caught hold of the human vehicle of the beggar woman and within two hours made her part with the pittance she had in favour of the man. The deity responded quickly, as being in the lower rungs of the cosmic ladder nearest to the earth-plane it was within easy reach of human beings; and its power was limited to grant only so much of money to the one who called for its assistance.
The Tantra recognizes the one Supreme Deity presiding over everything as the Highest, at the same time admitting the existence as the Highest, at the same time admitting the existence of various Gods and Goddesses. In the words of Sri Kapali Sastriar: “The sages of the Tantra do not see any inconsistency in the position, for they recognise that this creation is not a unitary system but a gradation of worlds spread over a rising tier of consciousness and planes and the various Gods and Goddesses are higher beings, powers and entities, deriving their authority from the Supreme to take their part and act or preside over their spheres of domain. There is a regular hierarchy of Gods some of whom are far above the highest heavens of human reach. But there are also Gods and Goddesses closer to the human level. They are more readily accessible to those who aspire to them and in some cases the seeker on the Tantric path looks to the aid and lead of these deities in his effort. They are endowed with capacities and powers beyond normal human possibility, but they are not all for that reason divine in nature. There are higher and lower classes of them, UCCA and ksudra devatas. Those that are nearest to the earthplane, swarming in the vital world overtopping the physical, are usually of the latter type. They respond very readily to the approaches of those who seek their help but they do so mainly for their own purpose, namely, to get hold of the particular human vehicle and convert it into a centre for their activity on the earth. They may and do answer the call of the seeker in the beginning but in the end they let him down, rather roughly, once their purpose is fulfilled. The seeker is misled; his inner progress comes to a standstill if it does not end in disaster. The Kshudra Devatas mislead the seeker with petty glamorous gifts, induce a false sense of progress and siddhi, prevent the dawn of real jnana which would expose their whole game and succeed in enslaving the man for their purpose at the cost of his soul which is betrayed into misadventure”.
Bu there are also entities of a higher order, benevolent deities, Uccha Devatas and as they occupy higher levels, the seeker has to make an effort to ascent to them. But they take the seeker on the path steadily and safely and ultimately do him the utmost good. There are still higher deities with cosmic functionings nearer to the Supreme Cosmic Godhead who presides over the myriad worlds that are created. Then at the top of this pyramidal structure of the cosmos spreading over an ascending tier of consciousness, at the summit of the innumerable levels and planes of existence there are certain cardinal Godheads, so many facets of the One truth, the Supreme Deity that correspond to the Brahman of the Upanishads. The spiritual disciplines leading to such cardinal Deities are known as Brahma Vidyas. These are also popular as Maha Vidyas, the great paths of discipline or Siddha Vidyas, the lines of quest where fulfillment is assured.
The Sanskrit word vidya is formed from the root vid to know or to understand. Vidya means learning or knowledge and also denotes the way to understanding, the path of knowledge, the Teaching. The mystics, all over the world, in their quest for the highest knowledge followed certain paths, undertook certain disciplines which were kept secret and were revealed only in the esoteric hierarchy of master and disciple. In India, the Upanishads, the repository of ancient wisdom and secret knowledge, mention in the body of their texts certain Vidyas, disciplines of knowledge. It has to be remembered that the Upanishads are not merely texts outlining the philosophical speculations of our ancient seers, as popularly held, but also manuals of Sadhana, practical guide-books on spiritual quest. These are the records of jottings of the reaching the ancient seekers had from their masters, an aid-memoire to remember the direct realizations they had in pursuing various disciplines of knowledge in their Sadhana. Likewise in the Tantra which is acclaimed as the great Sadhana Shastra, a practical manual, we find the great disciplines of knowledge, Maha Vidyas, occupying an important place. Especially where the Supreme is adored as the Great Primordial Goddess, the Tantra classifies the disciplines leading to the cardinal Deities as dasa maha vidyas, the ten great paths of knowledge. These cardinal deities are the ten outstanding personalities of the Divine Mother. Their great names are: Kali, Tara, Tripurasundari, Bhuvaneshwari, Tripura Bhairavi, Chinnamasta, Dhumavati, Bahalamukhi, Matangi and Kamalatmika.
What may be the precise significance of classifying the Vidyas into ten will be a difficult question to answer. But we can indicate the following: The Supreme Mother is the Transcendent Absolute ineffable immutable. In the act of creation, she subjects herself to time and space. Though the space is actually one vast stretch, for our grasp and understanding, we demarcate the indivisible and infinite Space into ten directions, east, west, south, north, south-east, south-west, north-east, north-west, above and below. Similarly the one infinite Mother is delineated as ten outstanding personalities. Again, knowledge is one and the consciousness is one and the same everywhere. But it is grasped and understood in ten different ways by the ten senses, skin, eye, ear, tongue, nose, mouth, foot, hand, anus and genital. Likewise, the one Truth is sensed in its ten different facets; the Divine Mother is adored and approached as the ten cosmic Personalities, Dasa Maha Vidyas. Each of these ten great Vidyas is a Brahma Vidya. The Sadhaka of any one of these Vidyas attains ultimately, if his aspiration is such, the supreme purpose of life, parama purusartha viz, self-realisation and God-realisation, realizing the Goddess as not different from one’s self. All these Vidyas are benevolent deities of the highest order and so do the utmost good to the seeker of the Vidya. For anyone who takes to any of these ten Vidyas, the Sadhana proceeds on sound lines and is safe and sure. It is not necessary at the beginning for the aspirant to have as his goal the highest aim of life. His aim most probably is the fulfillment of his immediate wants and for that he approaches the Deity. Once an aspirant takes to the Deity, the Deity takes upon itself the Sadhana. This is the characteristic of these Maha Vidyas. Whatever the seeker desires the Divine Mother fulfils it. In the process his devotion to the Deity becomes stronger and stronger and he learns to look upon the Deity for even the most trivial things in life, seeks its guidance at every step and knows to wait on its grace. There starts a living concourse, a concrete intimacy between the devotee and the Deity which is so absorbing and so enthralling that all desires, all aims of the devotee with which he started the Sadhana pale into significance. The whole perspective becomes different and there comes about a change in the attitude of the Sadhaka to life and things. There come about visible signs of communion, concrete evidences of contact, irresistible proofs of the Presence and the unmistakable touches of the Divine’s gracious hand in every happening and in every circumstance. What were at one time miracles become now common-place things and the whole life becomes a happy hastening towards the Supreme Goal.
Thus nothing short of Self-Realisation, atma saksatkara is the goal of the Vidyas. Of course much depends on the seeker and on his active participation, But even if the seeker stops in the middle of the path, he does not come to any harm. Only his progress is delayed. In the Sadhana there are many pitfalls. The baser emotions may hold sway or the ego may interfere at each stage. Once an aspirant has taken to any of these ten Vidyas, he has to succeed ultimately. He may fail in the present birth. The Vidya will make him take the thread of the Sadhana in the next birth and will continue to give the necessary push to the soul of the aspirant on its onward march. Even one step forward in the path of these Vidyas goes a long way towards the Goal. Nothing goes in vain. In fact, the Tantra categorically declares that only those who have been sufficiently prepared in the previous births can approach the precincts of these Vidyas. For them alone are these well-proven carefully laid-out paths. They are the chosen ones, the men with a mission, the indefatigable toilers on the uphill path of these disciplines of knowledge.
Because all these Vidyas lead to the ultimate Reality, it does not mean that they are all one and the same. Each Vidya is distinct and distinguishable from the Other. Each is a particular Cosmic function and each leads to a special realization of the One Reality. The might of Kali, the sound-force of Tara, the beauty and bliss of Sundari, the vast vision of Bhuvaneshwari, the effulgent charm of Bhairavi, the striking force of Chinnamasta, the silent inertness of Dhumavati, the paralysing power of Bagalamukhi, the expressive play of Matangi and the concord and harmony of Kamalatmika are the various characteristics, the distinct manifestations of the Supreme Consciousness that has made this creation possible. The Tantra says that the Supreme can be realised at these various points. According to one’s ability and aptitude, one realises the great Goddess, becomes identified with her in her might, in her striking force, in her paralysing power or in her beauty and bliss, in her concord and harmony. If one wants to bathe in a river, one cannot bathe in the whole river; one has to bathe at a spot. Similarly if an aspirant wants to reach the Divine, circumscribed as he is by his receptivity and capacity, he chooses one particular path, takes up for adoration one aspect of the Divine. As his pursuit is exclusive, his progress is quick and his approach becomes direct. Ultimately he attains a perfect identification with the Divine.
But it is not the intention of the Tantra to limit the capacity of the individual to a particular realisation however perfect it may be. It is true that there are ten Maha Vidyas directly leading to the Supreme Truth, ten chalked out paths, safe and sure to have an immediate and direct approach. For instance if one takes to the Sadhana of the Maha Vidya, Chinnamasta, ultimately one attains a perfect identification with the Supreme. All the same it is a partial identification for Chinnamasta is one facet of the many-faceted Supreme. Not a particular realisation, but a global realisation is required to attain the Total Divine. Pursuing our analogy of bathing in a river, if one wants to have conception of the ebb and flow, the eddies and currents of a river one has to bathe at various spots in the river. This is exactly what one does when one takes a holy bath in a sacred place. For instance, in Kashi, baths in so many bathing ghats are prescribed in order that the bather may have a full realisation of the grandeur of the Divine Ganges. Similarly in these ten great disciplines of knowledge, the seeker can aspire for an integral knowledge and he may, depending on his capacity, come nearer the Total Divine, by having as many realisations as he can.
In fact, the Tantra which is justly famous as a science of synthesis holds that one Maha Vidya leads its Sadhaka to another depending on the need and aspiration of the Sadhaka. The worshipper of Kali has a unique realisation of the Divine, the Terrible. At the same time, the realisation of the Divine, the Auspiscious is available to him if he understands the concept of bhadra kali. Then he goes on to appreciate the correspondence between the other two Vidyas, Tripurasundari and Tripurabhairavi, Tripura the beautiful and Tripura the terrific. In the Sundari Vidya itself worship is prescribed for Mantrini and Dandanatha, the attendants of Lalita Tripurasundari. Mantrini is Syamala or Matangi and Dandanatha corresponds to Bagalamukhi.
Thus the Vidya of Tripurasundari brings to the aspirant the realisations pertaining to the Vidyas of Matangi and Bagalamukhi.
Here a word of caution is necessary. When it is said that the Vidyas of Matangi and Bagalamukhi are implied in the Vidya of Sundari, the human mind immediately jumps to the conclusion that the Vidya of Sundari is superior to the other two Vidyas. The mind of man subject to the limitations of time and space can understand anything only in relation to time and space. Any new knowledge is immediately related to the old, classified and docketed as anterior or posterior, higher or lower. We reiterate that each of the ten Vidyas leads the seeker to the Supreme Reality. Each is great in its own right and each is equal in all respects to each of the other nine Vidyas. The practices of certain disciplines are widely prevalent, others are less known. For that matter they are not less important.
Again, an integral realisation is possible in these Vidyas because though they are distince and unique, they have among themselves many characteristics in common. Kali, Chinnamasta, Dhumavati and Bagalamukhi have the common characteristics of Power and Force, active or dormant. Sundari Bhuvaneshwari, Bhairavi, Matangi and Kamalatmika share the qualities of Light, Delight and Beauty. Tara has certain characteristics of Kali and certain others of Sundari and is correlated to Bhairavi, Bagalamukhi and Matangi in the aspect of Sound-Force expressed or impeded. Thus the ten Maha Vidyas fall into three broad divisions of discipline. The Veda lauds three Goddesses, producers of delight, tisro devir mayobhuvah. The Upanishads mention the One unborn, red, white and dark ajam ekam lohita sukla krsnam. The Tantras speak of Kali, the dark, Tara the white and Sundari the red.
In this ancient land, for ages the worship of these great mighty Personalities of the Mother has been prevalent. The other Vidyas have been practised but they have not come into the lime light. In the southern part of India the Vidya of Sundari, Sri Vidya, has been much in vogue. In the far north and north-west, in Tibet and in Kashmir adoration of Tara is popular. In the north-east parts of the country, especially in Bengal, the cult of Kali is famous. Thus the whole of India is full of adoration for the Divine Mother and the spirit of India has been eternally sustained by the Force Supreme, para sakti. The might of Kali, the wisdom of Tara and the beauty of Sundari have forged and fashioned this ancient race where the first man, the offspring of manu, the thinker, dared to peer with his earthly eyes into the portals of the Beyond.
We shall now take up for the study the respective Vidyas.
Mahavidyas and Avatars of Vishnu
Source: http://shanmatha.blogspot.com/2009/09/dasavatharam-dasamahavidya.html
You wont find any puranic lore for the relation between these Vidyas and Avatharas but the logic of putting the Dasamahavidya with the Dasavataram is related thru perception and thru the Tanric interpretation.
If watched carefully one can find the theory of evolution in the Dasaavathara.
The same way the Dasamahavidyas represent the evolution of the Soul.The First Avatara in an 100% aquatic fish and the Last is the Man of Purnathvam(complete) – Kalki.
– from a fish to a complete man..Similarly as Nirguna Swaroopi, she is Kali of Darness;
As Saguna roopi she is Sundari of ultimate Gnana(wisdom)A sloka from Lalita Sahasranama says “karanguli nakhotpanna Narayana dasa kritih” that from the nails of the ten fingers of the Devi emerged the ten manifestations of Narayana as Dasavataram.
The ten manifestations of devi as Kali, Tara, Tripurasundari, Bhairavi, Bhagalamuki, CHinnamasta, Doomavati, Kamala, Bhuvaneswari and Matangi embody a whole range of attitudes gracious and awesome, benign and destructive. The same force called “Shakti” is the motivational force for the ten incarnations of Vishnu.
She is Vishnu and He is Devi; There is no difference between them.
These comparisons only mean that Amba’s being non-different from Narayana and need not be taken literally.
https://sarwamangala.com/Dasamaha.html
Todala Tantra equates Vishnu‟s ten incarnations with the ten Mahavidyas as follows: “Shri Devi said: Lord of Gods, Guru of the universe, tell me of the ten avatars. Now I want to hear of this, tell me of their true nature. Paramesvara, reveal to me which avatar goes with which Devi. “Shri Shiva said: Tara Devi is the blue form, Bagala is the tortoise incarnation, Dhumavati is the boar, Chinnamasta is Nrisimha, Bhuvaneshvari is Vamana, Matangi is the Rama form, Tripura is Jamadagni, Bhairavi is Balabhadra, Mahalakshmi is Buddha, and Durga is the Kalki form. BhagavatÌ Kali is the Krishna murti.” (Todalatantra 10)
The worship of these is also prescribed as an astrological remedy – for the 9 planets and the Lagna as follows: Kali for Saturn, Tara for Jupiter, Maha Tripura Sundari (or Shodasi-Sri Vidya) for Mercury, Bhuvaneshvari for Moon, Chinnamasta for Rahu, Bhairavi for Lagna, Dhumavati for Ketu, Bagalamukhi for Mars, Matangi for Sun, and Kamala for Venus.
Source: my own compilation

Mahavidya Yantras
Source: Dasa Mahavidya Yantras
Source: Dasa Mahavidya Yantras

Source: Dasa Mahavidya Yantras
Source: Dasa Mahavidya Yantras

Source: Dasa Mahavidya Yantras

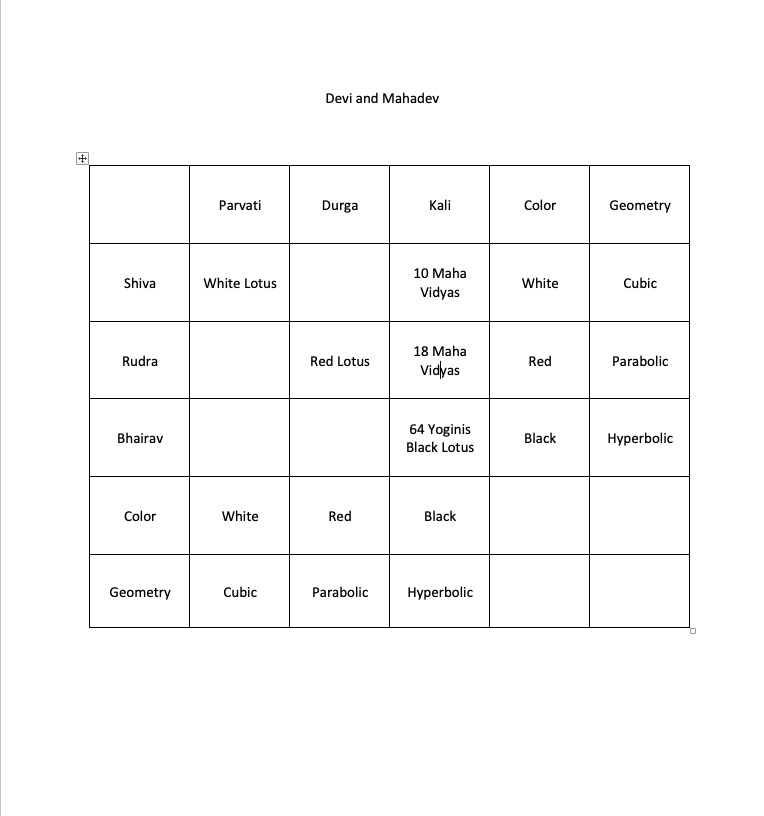
Source: Author’s own work
My Related Posts
Chausath (64) Yogini Hindu Temples Architecture
Sapta Matrikas (Seven Mothers) and Cosmology
Hierarchy Theory in Biology, Ecology and Evolution
Key Sources of Research
Das Mahavidyas – The 10 Tantric Goddesses of Wisdom
Written By Swami Ayyappa Giri
Kriya Tantra Institute
https://kriyatantrainstitute.com/articles/mahavidyasadhana
Goddess Worship in Hinduism: The Ten Wisdom Goddesses of Shaktism
Aishwarya Javalgekar
2012
https://www.academia.edu/32388291/Goddess_Worship_in_Hinduism_The_Ten_Wisdom_Goddesses_of_Shaktism
Dus Mahavidyas – the Ten Forms of the Devi
Ganesh Kumar
https://www.academia.edu/5923232/Dus_Mahavidyas_the_Ten_Forms_of_the_Devi
Ten Mahavidyas-Manifestations Of Cosmic Female Energy
Exotic India
2010, Exotic India Art
https://www.academia.edu/50890236/Ten_Mahavidyas_Manifestations_Of_Cosmic_Female_Energy
Wisdom Goddesses – Mahavidyas and the Assertion of Femininity in Indian Thought
May 2002
Nitin Kumar
Editor http://www.exoticindia.com
https://www.exoticindiaart.com/article/mahavidyas/
About Mahavidya The 10 Forms of Goddess Shakti | Adi Parashakti
https://templesinindiainfo.com/about-mahavidya-the-10-forms-of-goddess-shakti/
Tantric Visions of the Divine Feminine: The Ten Mahāvidyās
By David R. Kinsley
Book
Dasa Mahavidya & Tantra Sastra
Sarbeswar Satpathy
Punthi Pustak, 1992
Book
https://www.exoticindiaart.com/book/details/dasamahavidya-ten-mahavidyas-and-tantrasastra-nag414/
Śakti Iconography in Tantric Mahāvidyās
Sarbeswar Satpathy
Punthi Pustak, 1991
Book
Dasa Mahavidya (Tantrasara)
Yogiraj Yashpal Bharti
Book, Hindi
Dasamahavidya-Mimamsa
Author(s): Vishnu Datta Rakesh
ISBN: 9788174531445
Year of Publication: 2004
Bibliographic Information: 218p
Language: English
Book
https://www.vedicbooks.net/dasamahavidyamimamsa-p-16126.html
Tantric Yoga and the Wisdom Goddesses: Spiritual Secrets of Ayurveda
David Frawley
Lotus Press, 1994
Book
Change, Continuity and Complexity: The Mahāvidyās in East Indian Śākta Traditions
By Jae-Eun Shin
Book
Transformations and Transfer of Tantra in Asia and Beyond
edited by István Keul
Book
The Mahavidyas: The Powers of Consciousness Conceptualized – Part 1
By Devadatta Kali
Vedanta Society
The Mahavidyas: The Powers of Consciousness Conceptualized – Part 2
By Devadatta Kali
Vedanta Society
Dasa Mahavidya – The Ten Great Wisdoms
Posted on June 19, 2019 by Rati Mehrotra
Das Mahavidyas Presentation
Story of the Origin of the Das Mahavidyas
Dasa Mahavidya
Man blunder
https://manblunder.com/articles/dasa-mahavidya
Dus Mahavidyas
https://www.rudraksha-ratna.com/articles/dus-mahavidyas
Dasha Mahavidya – Part One – Part Four
sreenivasarao’s blogs
The Ten Great Cosmic Powers (Dasa Mahavidyas)
By S.Shankaranarayanan
November 2013
Book
samatabooks@gmail.com
Das Mahavidyas
Gita Press, Gorakhpur
Book, Hindi
https://archive.org/details/HindiBookDashaMahavidyaByGitaPress
Dasha Mahavidya and the 10 dimensions
December 15, 2019
Dasa Mahavidya
Orissa Review 2009
Dasa Maha Vidya: The Ten Wisdom Goddesses
Sahasrakshi
Dasa Mahavidya
Vinita Rashinkar
2020
The Dasa Mahavidyas
Chamunda Swami ji
Das Mahavidya book set (दस महाविद्द्या)
- Author – Goswami Prahlad Giri
- Publisher – Choukhamba Krishnadas Academy
- Language – Hindi and Sanskrit
Dasa Mahavidyas: the Manifestations of Cosmic Female Energy
Atmanism
Dasa Mahavidya Yantras
Varahamihira
http://varahamihira.blogspot.com/2004/09/dasa-mahavidya-yantras.html
Reaching GODHOOD
– SREEVIDYA –
Ten Goddesses / Dasamahavidya
Dasha(10) Mahavidya
(SriVidya aka BrahmaVidya aka ShuddhaVidya)
Learn Kriya Yoga
The Dasa(Ten) Mahavidyas
Hindu Online
Click to access dasamahavidya.pdf
Dasha Maha Vidya: Wisdom from the Ten Directions
Sai Venkatesh Balasubramanian
Bengaluru, India: saivenkateshbalasubramanian@gmail.com
Dus Mahavidyas
the Ten Forms of the Devi
Dolls of India
Dasa Mahavidya – The 10 aspects of Adi Parashakti
Dasha Mahavidya – The Ten Great Sources of Wisdom
Sabda Institute
Maha Vidya
Wikipedia