Seeds and Mountains: The Cosmogony of Temples in South Asia

Key Terms
- Viraj
- Purusha
- Hindu Temple
- Architecture
- Purush Sukta
- Rg Veda
- Creation Myth
- Hinduism
- Vedic Philosophy
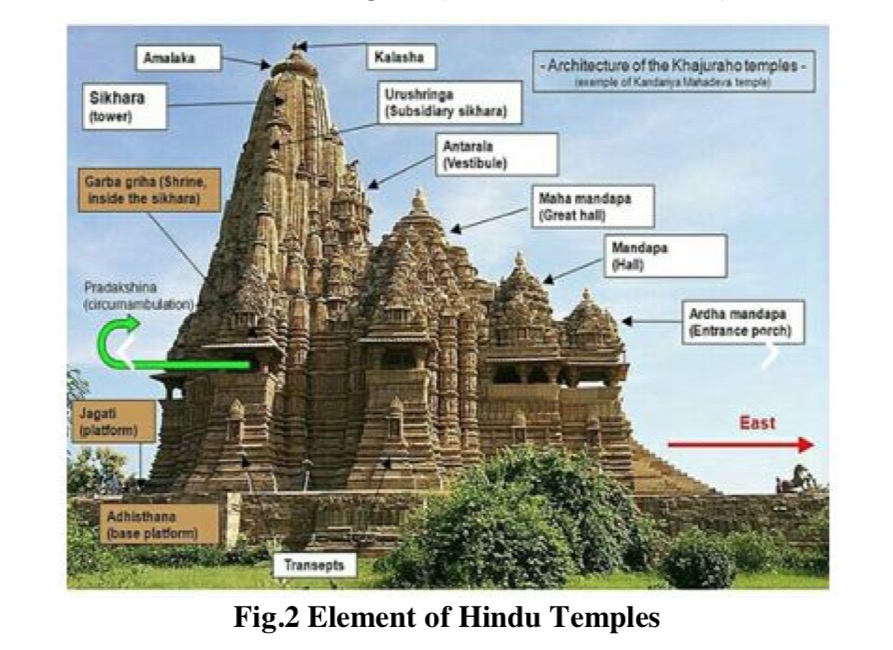
- Amalaka
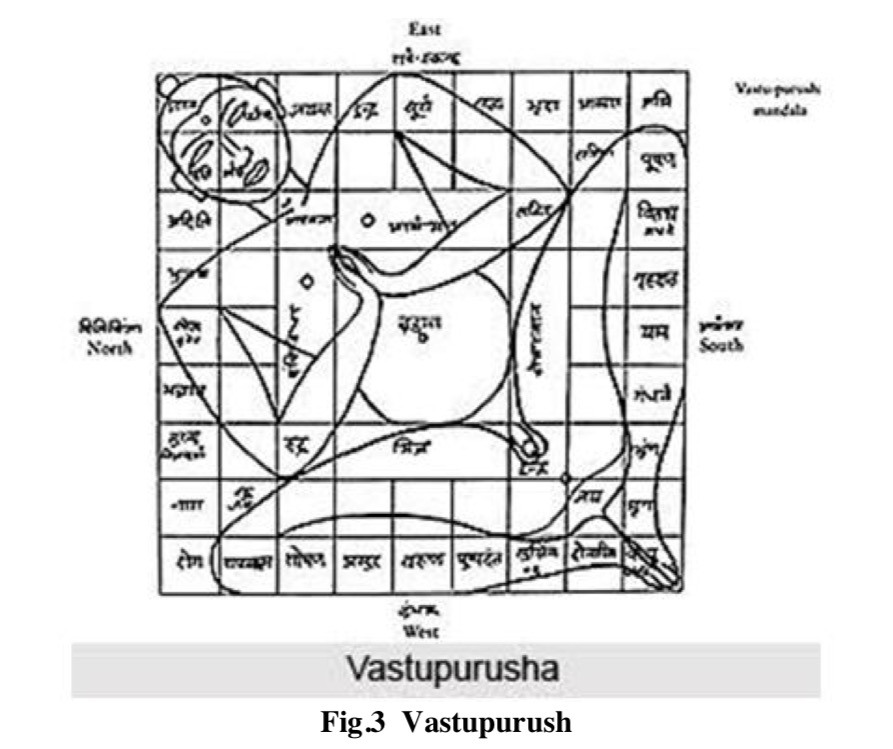
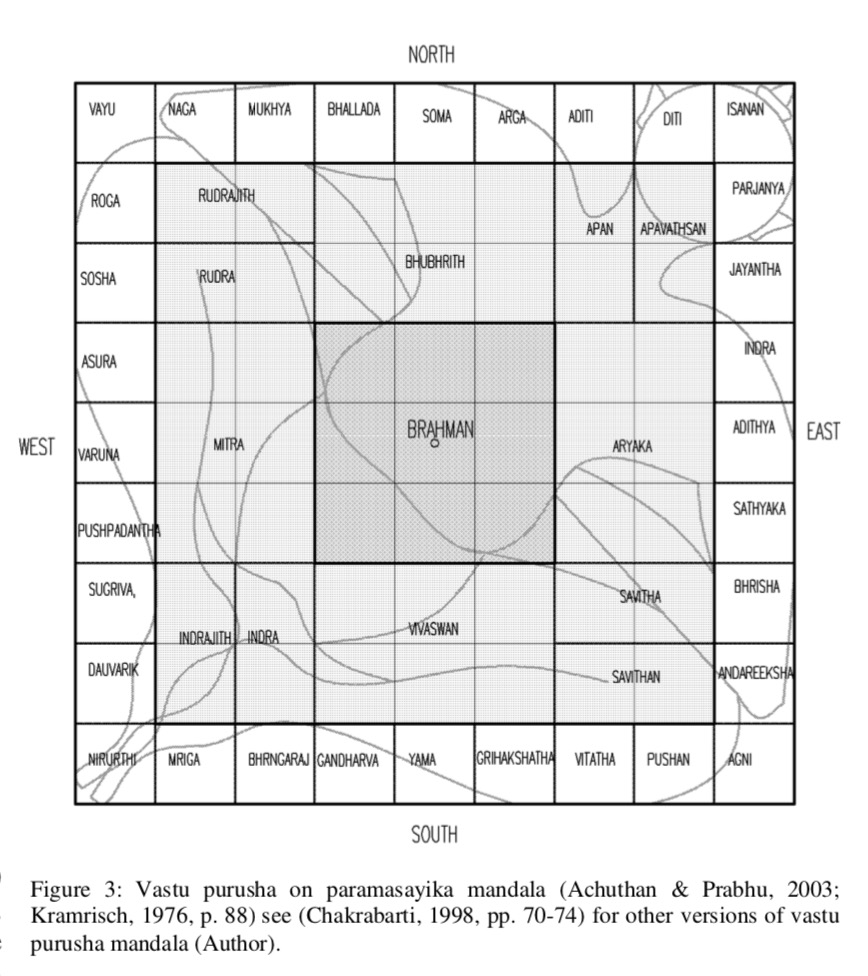
- Vastupurush Mandala
- Amalaka Ekadashi
- Gavaksa
- Kumbha
- Kalash
- Shakti
- Prakriti
- Amla Fruit
- Square and Circle
- Circling the Square
- Squaring the Circle
- Heaven and Earth
Researchers
- Adam Hardy
- Stella Kramrisch
- Alice Boner
- Michael W Meister
- George Michell
- Ananda K. Coomaraswamy
- Madhusudan A. Dhaky
- Vasu Renganathan
- Brown, Percy
- Subhash Kak
- Datta, Sambit
- Sonit Bafna
- Zimmer, Heinrich
- Pramod Chandra
- Krishna Deva
THE TEMPLE AS PURUSA
Source: THE TEMPLE AS PURUSA

Source: THE TEMPLE AS PURUSA

Source: THE TEMPLE AS PURUSA

Source: THE TEMPLE AS PURUSA

Source: THE TEMPLE AS PURUSA

Source: THE TEMPLE AS PURUSA

Source: THE TEMPLE AS PURUSA

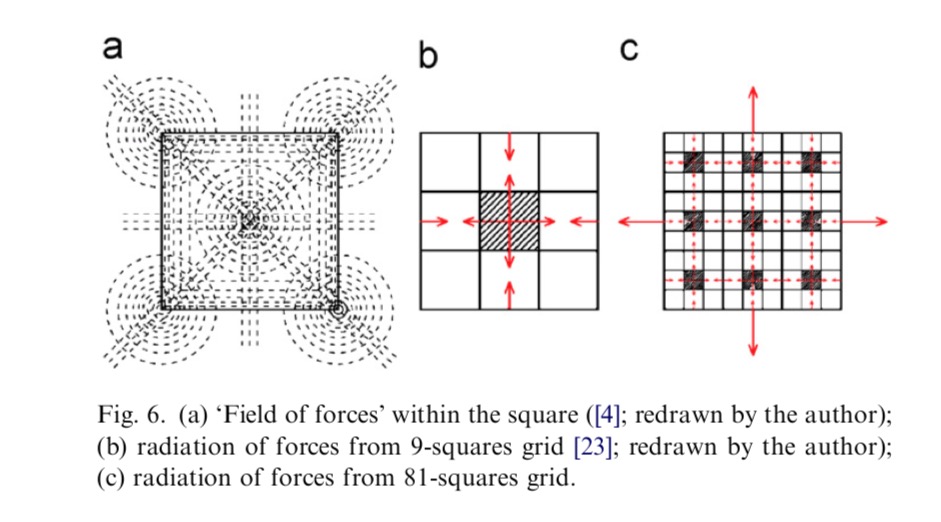
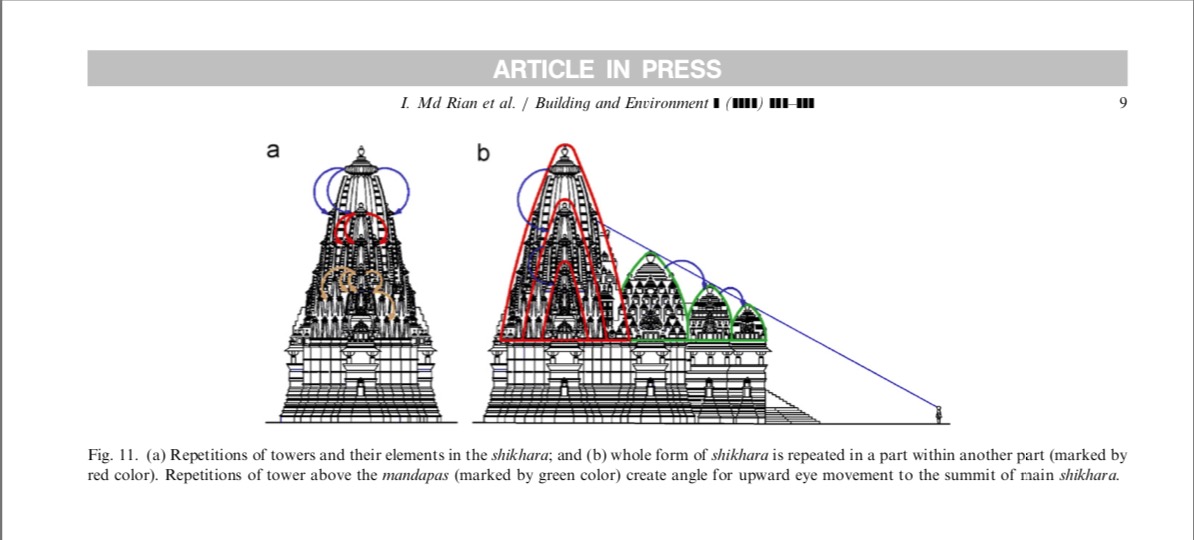
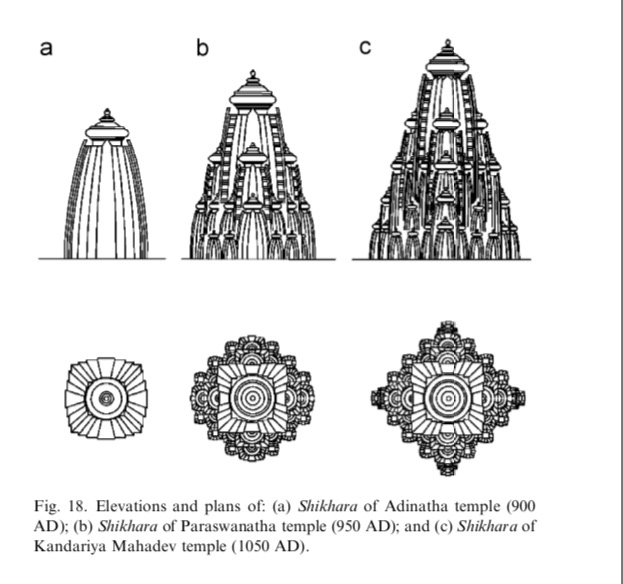
Seeds and Mountains: The Cosmogony of Temples in South Asia
Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

Source: Seeds and Mountains: The Cosmogony of Temples in South Asia

My Related Posts
You can search for these posts using Search Posts feature in the right sidebar.
- Temples of the Indus: Studies in the Hindu Architecture of Ancient Pakistan
- Art and Architecture of Gandhara Buddhism
- An Infinity of Stupas: Design and Architecture of Chinese Buddhist Temples and Pagodas
- Design Principles of Early Stone Pagodas in Ancient Korean Architecture
- The Architecture and Sacred Temple Geometry of Japanese Buddhist Temples
- Nichiren School of Buddhist Philosophy
- Pure Land School of Buddhist Philosophy
- Shingon (Esoteric) School of Buddhist Philosophy
- Three Treatise School (Sanlun) of Chinese Buddhist Philosophy
- Hua Yan Buddhism : Reflecting Mirrors of Reality
- What is Yogacara Buddhism (Consciousness Only School)?
- Dhyan, Chan, Son and Zen Buddhism: Journey from India to China, Korea and Japan
- Chinese Tiantai and Japanese Tendai Buddhism
- Intersubjectivity in Buddhism
- Schools of Buddhist Philosophy
- Meditations on Emptiness and Fullness
- Self and Other: Subjectivity and Intersubjectivity
- Law of Dependent Origination
- The Fifth Corner of Four: Catuskoti in Buddhist Logic
- Square and Circle of Hindu Temple Architecture
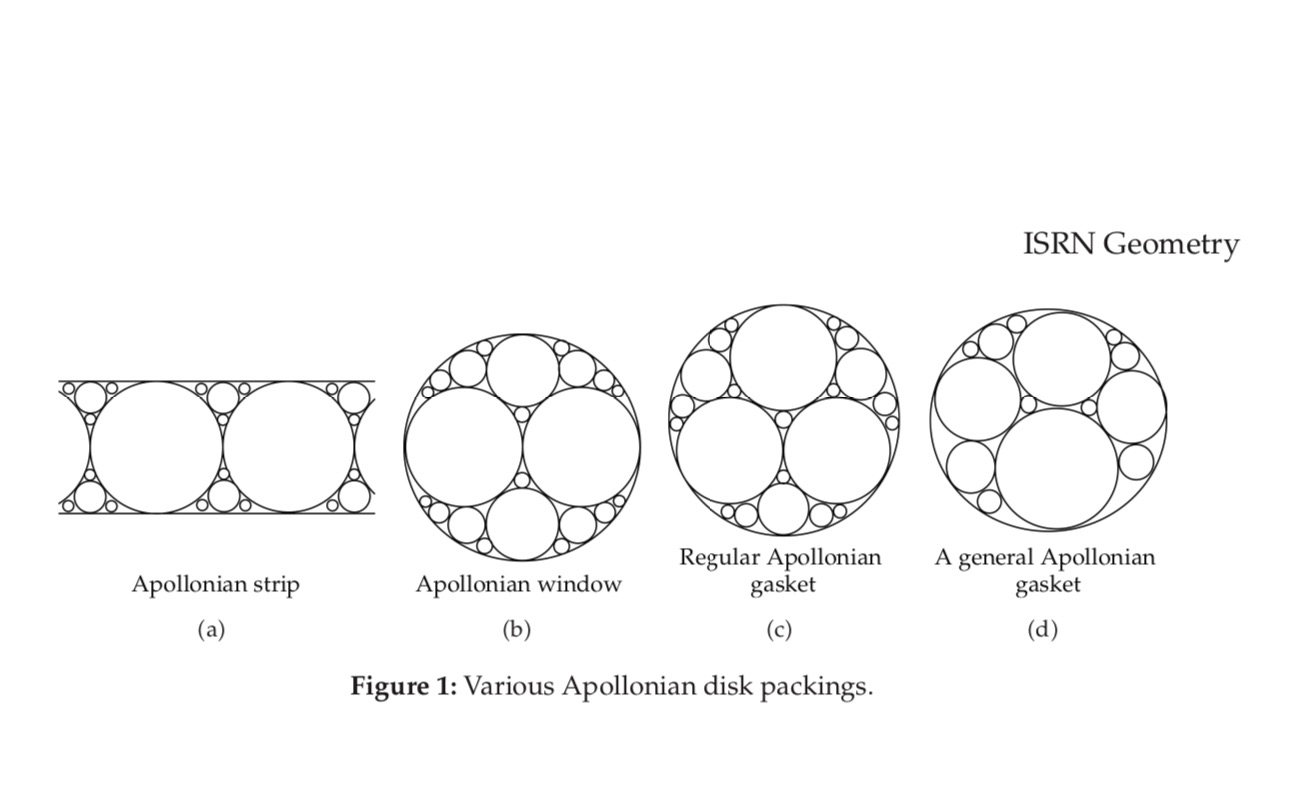
- Indira’s Pearls: Apollonian Gasket, Circle and Sphere Packing
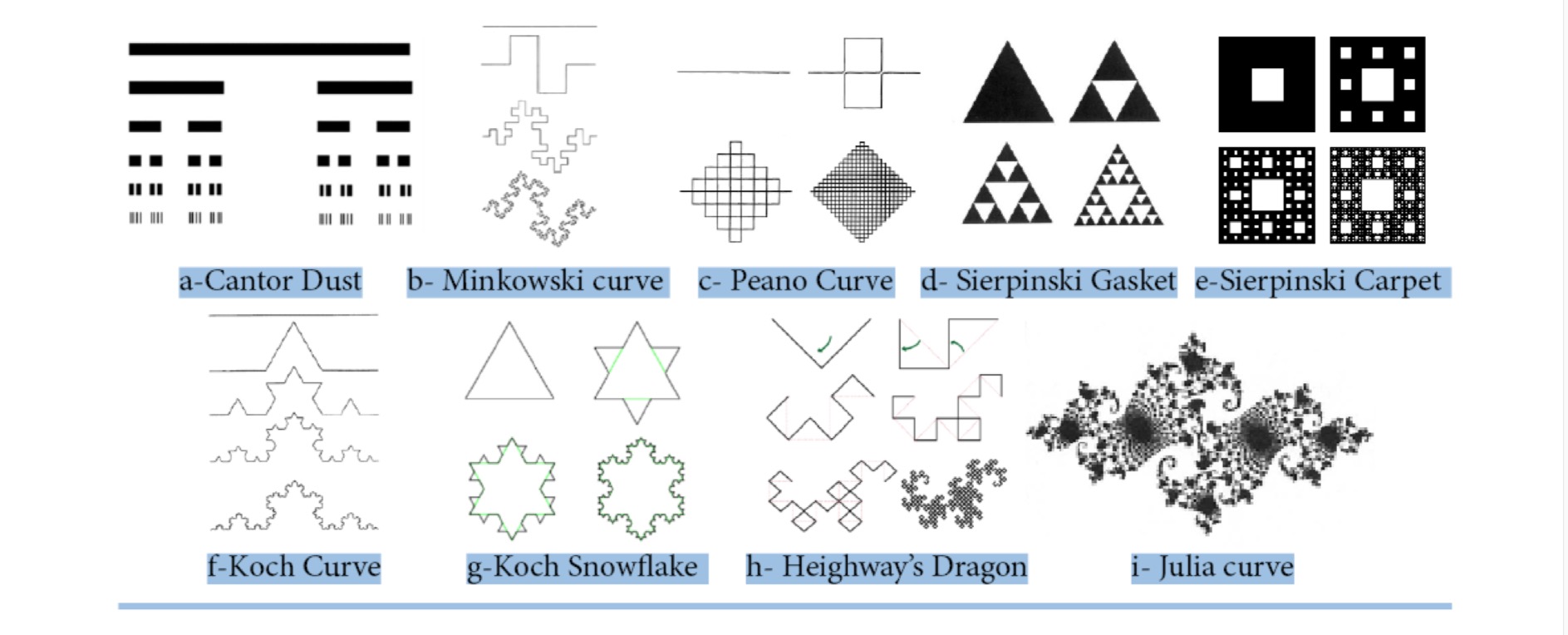
- Cantor Sets, Sierpinski Carpets, Menger Sponges
- Fractal Geometry and Hindu Temple Architecture
- The Great Chain of Being
- INTERCONNECTED PYTHAGOREAN TRIPLES USING CENTRAL SQUARES THEORY
- The Pillar of Celestical Fire
- Purush – The Cosmic Man
- Platonic and Archimedean Solids
- Fractal and Multifractal Structures in Cosmology
Key Sources of Research
Seeds and Mountains: The Cosmogony of Temples in South Asia
2013, HEAVEN ON EARTH TEMPLES, RITUAL, AND COSMIC SYMBOLISM IN THE ANCIENT WORLD
https://www.academia.edu/3658884/Seeds_and_Mountains_The_Cosmogony_of_Temples_in_South_Asia
Studies in Indian Temple Architecture
1976, Artibus Asiae
PARTS AND WHOLES: THE STORY OF THE GAVĀKSA
Adam Hardy
Vārāṭa Temples: The Lost Tradition In-Between
Adam Hardy

EARLY ARCHITECTURE AND ITS TRANSFORMATIONS: NEW EVIDENCE FOR VENACULAR ORIGINS FOR THE INDIAN TEMPLE
Michael W Meister
Indian Architecture
(Buddhist and Hindu Periods)
Percy Brown

Encyclopedia of Indian Temple Architecture
North India
Foundations of North Indian Style

Encyclopedia of Indian Temple Architecture
South India
Lower Dravidadesa

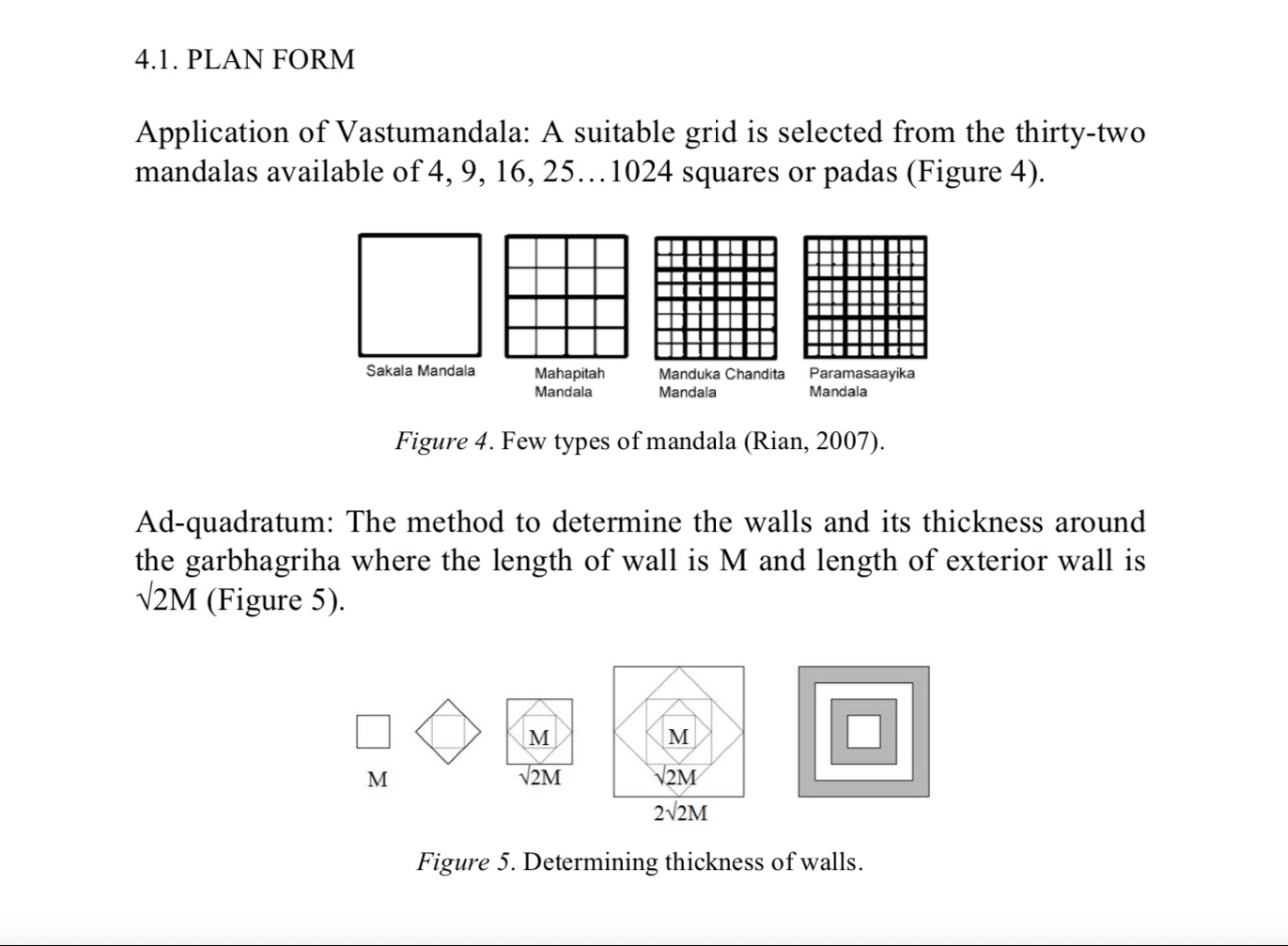
Vāstupuruṣamaṇḍalas: Planning in the Image of Man
In: Maṇḍalas and Yantras in the Hindu Traditions
Author: Michael W. Meister
Type: Chapter
Pages: 251–270
DOI: https://doi.org/10.1163/9789004492370_012
https://brill.com/display/book/9789004492370/B9789004492370_s012.xml
Maṇḍalas and Yantras in the Hindu Traditions
Series:
Brill’s Indological Library, Volume: 18
Author: Gudrun Bühnemann
E-Book (PDF)
Availability: Published
ISBN: 978-90-04-49237-0
Publication: 15 Nov 2021
Hardback
Availability: Published
ISBN: 978-90-04-12902-3
Publication: 30 Jun 2003
Michael W. Meister, M. A. Dhaky and Krishna Deva (ed.): Encyclopaedia of Indian temple architecture: North India: Foundations of North Indian style c. 250 b.c.–a.d. 1100. I: xvii, 422 pp. 158 figures, 15 maps; II: viii, 778 plates.
New Delhi: American Institute of Indian Studies, and Princeton: Princeton University Press, 1988.
Published online by Cambridge University Press: 24 December 2009
George Michell
Michael W. Meister. Review of “The Temple Architecture of India” by Adam Hardy
CAA Reviews
April 2008
DOI:10.3202/caa.reviews.2008.40
Authors:
Michael Meister
University of Pennsylvania
Early Indian Architecture and Art
Subhash Kak
Migration & Diffusion – An international journal, Vol.6/Nr.23, 2005, pages 6-27
Encyclopedia of Indian Temple Architecture, North India, Volume II, Part I: Foundations of North Indian Style.
(Two books: text and plates)
(ENCYCLOPAEDIA OF INDIAN TEMPLE ARCHITECTURE) First Edition
by Michael W. Meister (Editor), Madhusudan A. Dhaky (Editor)
Publisher : Princeton University Press; First Edition (October 21, 1989)
Language : English
Hardcover : 816 pages
ISBN-10 : 0691040532
ISBN-13 : 978-0691040530
Drāviḍa Temples in the Samarāṅgaṇasūtradhāra
Adam Hardy
Encyclopedia of Indian Temple Architecture – North and South India (Eight Volumes in 16 Books)
| AUTHOR: | MICHAEL W. MEISTER, GEORGE MICHELL, M. A. DHAKY |
| PUBLISHER: | AMERICAN INSTITUTE OF INDIAN STUDIES |
| LANGUAGE: | ENGLISH |
| EDITION: | 1986 – 2001 |
Hardy, “The Temple Architecture of India” review
Michael W Meister
Published 2008
https://www.academia.edu/5688611/Hardy_The_Temple_Architecture_of_India_review
“Geometry and measure in Indian temple plans: Rectangular temples.”
Meister, Michael W..
Artibus Asiae 44 (1983): 266. DOI: 10.2307/3249613
Measurement and proportion in Hindu temple architecture
1985, Interdisciplinary science reviews
Tradition and Transformation: Continuity and Ingenuity in the Temples of Karnataka
Adam Hardy
2001, The Journal of the Society of Architectural Historians
De- and Re-constructing the Indian Temple.
Meister, M. W. (1990).
Art Journal, 49(4), 395–400. https://doi.org/10.1080/00043249.1990.10792723
https://architexturez.net/doc/az-cf-175759
https://www.tandfonline.com/doi/pdf/10.1080/00043249.1990.10792723
Re-creation and self-creation in temple design
Architectural Research Quarterly
Dependence and Freedom in the Theory and Practice of Indian Temple Architecture
2023, Embodied Dependencies and Freedoms: Artistic Communities and Patronage in Asia
2013 – Indian Temple Typologies
Adam Hardy
Kashmiri Temples: a Typological and Aedicular Analysis
Adam Hardy
2019, Indology’s Pulse: Arts in Context (Essays Presented to Doris Meth Srinivasan in Admiration of Her Scholarly Research) edited by Corinna Wessels-Mevissen and Gerd J. R. Mevissen
Mandala and Practice in Nagara Architecture in North India
Michael W Meister
Published 1979
Building science of Indian temple architecture
Published 2013
Prāsāda as Palace: Kūṭina Origins of the Nāgara Temple
Michael W Meister
1988, Artibus Asiae
https://www.jstor.org/stable/3250039
On the Development of Indian Temple Architectural Morphology and the Origin of Superstructure
Vasu Renganathan
Published 2007
On the development of a morphology for a symbolic architecture: India
1986, RES: Anthropology and Aesthetics
Symbol and Surface: Masonic and Pillared Wall-Structures in North India
Artibus Asiae
A Note on the Superstructure of the Marhia Temple
Michael W Meister
1974, Artibus Asiae
Indo-Aryan’ Temples: Noodling Seventh-Century Nagara
Michael W Meister
JISOA ns vol. 27
Region, Style, Idiom, and Ritual in History
Michael W. Meister on the Study of Jain Art
John E. Cort
Chakshudana or Opening the Eyes
Seeing South Asian Art Anew
Edited by Pika Ghosh and Pushkar Sohoni
First published 2024
ISBN: 978- 1- 032- 20783- 4 (hbk)
ISBN: 978- 1- 032- 27121- 7 (pbk)
ISBN: 978- 1- 003- 29147- 3 (ebk)
DOI: 10.4324/ 9781003291473- 3
Mountains and cities in Cambodia: Temple architecture and divine vision.
Meister, M.W.
Hindu Studies 4, 261–268 (2000). https://doi.org/10.1007/s11407-000-0009-2
https://link.springer.com/article/10.1007/s11407-000-0009-2
https://www.jstor.org/stable/20106740

References cited
- Boisselier, Jean. 1997. The meaning of Angkor Thom. In Helen Ibbitson Jessup and Thierry Zephir, eds., Sculpture of Angkor and ancient Cambodia: Millennium of glory, 117–22. London: Thames and Hudson.Google Scholar
- Coomaraswamy, A. K. 1992. Early Indian architecture, I–IV. In Michael W. Meister, ed., Ananda K. Coomaraswamy: Essays in early Indian architecture, 3–69, 105–24. Delhi: Oxford University Press.Google Scholar
- Coomaraswamy, A. K. 1993 [1928–31]. Yakṣas: Essays in the water cosmology (ed. Paul Schroeder). Delhi: Oxford University Press.Google Scholar
- Dagens, Bruno. 1997. Angkor: ‘The city on the Ganges.’ Connaissance des arts [special exhibition issue] pp. 23–24.
- Giteau, Madeleine. 1997. The profound sense of the sacred. Connaissance des arts [special exhibition issue] pp. 42–57.
- Groslier, Bernard Philippe 1962. Indochina: Art in the melting-pot of races. London: Methuen.Google Scholar
- Jessup, Helen Ibbitson. 1997. Temple-mountains and the Devarāja cult. In Helen Ibbitson Jessup and Thierry Zephir, eds. 1997. Sculpture of Angkor and ancient Cambodia: Millennium of glory, 101–16. London: Thames and Hudson.Google Scholar
- Jessup, Helen Ibbitson and Thierry Zephir, eds. 1997. Sculpture of Angkor and ancient Cambodia: Millennium of glory. London: Thames and Hudson.Google Scholar
- Meister, Michael W. 1979. Maṇḍala and practice in Nāgara architecture in North India. Journal of the American Oriental Society 99, 2: 204–19.Article MathSciNet Google Scholar
- Meister, Michael W. 1984. Śiva’s forts in central India: Temples in Dakṣiṇa Kosala and their ‘daemonic’ plans. In Michael W. Meister, ed., Discourses on Śiva: Proceedings of a symposium on the nature of religious imagery, 119–42. Philadelphia: University of Pennsylvania Press.Google Scholar
- Meister, Michael W. 1986a. Measurement and proportion in Hindu temple architecture. Interdisciplinary science reviews 10, 3: 248–58.Google Scholar
- Meister, Michael W. 1986b. On the development of a morphology for a symbolic architecture: India. Res, anthropology, and aesthetics 12: 33–50.Google Scholar
- Meister, Michael W. 1989. Prāsāda as palace: Kūṭina origins of the nāgara temple. Artibus Asiae 49, 3–4: 254–80.Google Scholar
- Meister, Michael W. 1990. De- and re-constructing the Indian temple. Art journal 49, 4: 395–400.Article Google Scholar
- Meister, Michael W. 1991. The Hindu temple: Axis and access. In Kapila Vatsyayan, ed., Concepts of space, ancient and modern, 269–80. New Delhi: Abhinav.Google Scholar
- Meister, Michael W. 1992. Symbology and architectural practice in India. In Emily Lyle, ed., Sacred architecture in the traditions of India, China, Judaism, and Islam, 5–24. Edinburgh: Edinburgh University Press.Google Scholar
- Meister, Michael W. 1996. Reassessing the text. In Farooq Ameen, ed., Contemporary architecture and urban form: The South Asian paradigm, 88–100. Bombay: Marg.Google Scholar
- Meister, Michael W. and M. A. Dhaky, eds. 1983. Encyclopaedia of Indian temple architecture: South India, lower Drāviḍadeśa. Philadelphia: University of Pennsylvania Press.Google Scholar
- Meister, Michael W., M. A. Dhaky and Krishna Deva, eds. 1988. Encyclopaedia of Indian temple architecture: North India, foundations of North Indian style. Princeton: Princeton University Press.Google Scholar
- Menon, C. P. S. 1932. Early astronomy and cosmology: A reconstruction of the earliest cosmic system. London: G. Allen & Unwin.Google Scholar
- Muschamp, Herbert. 1997. The designs of a genius redesigning himself. The New York times 18 July: C1, 29.
- Zimmer, Heinrich. 1983 [1955]. The art of Indian Asia. 2 vols. Princeton: Princeton University Press.Google Scholar
Constructing Community: Tamil Merchant Temples in India and China, 850-1281
Lee, Risha
https://doi.org/10.7916/D8W95H8W
https://academiccommons.columbia.edu/doi/10.7916/D8W95H8W
This dissertation studies premodern temple architecture, freestanding sculpted stones, and Tamil language inscriptions patronized by south Indian merchants in south India and China. Between the ninth and thirteenth centuries, Indian Ocean trade was at its apex, connecting populations on European and Asian continents through complex interlocking networks. Southern India’s Tamil region, in particular, has been described as the fulcrum of the Indian Ocean circuit; however, knowledge of intra-Asian contact and exchange from this period has been derived mostly from Arabic and Chinese sources, which are abundant in comparison with the subcontinent’s dearth of written history. My project redresses this lacuna by investigating the material culture of Tamil merchants, and aims to recover their history through visual evidence, authored by individuals who left few written traces of their voyages across the Indian Ocean.
The arguments of my dissertation are based primarily on unpublished and unstudied monuments and inscriptions, weaving together threads from multiple disciplines–art history, literature, epigraphy, and social theory–and from across cultures, the interconnected region of the eastern Indian Ocean and the South China Seas, spanning the Sanskritic, Tamil, Malay, and Sinocentric realms. My dissertation challenges traditional narratives of Indian art history that have long attributed the majority of monumental architecture to royal patrons, focusing instead on the artistic production of cosmopolitan merchants who navigated both elite and non-elite realms of society. I argue that by constructing monuments throughout the Indian Ocean trade circuit, merchants with ties to southern India’s Tamil region formulated a coherent group identity in the absence of a central authority.
Similar impulses also are visible in merchants’ literary production, illustrated through several newly translated panegyric texts, which preface mercantile donations appearing on temple walls in the modern states of Tamil Nadu, Karnataka, and Andhra Pradesh. Moreover, my work analyzes the complex processes of translation visible in literary and material culture commissioned by merchants, resulting from inter-regional and intercultural encounters among artisans, patrons, and local communities. Rather than identifying a monolithic source for merchants’ artistic innovations, in each chapter I demonstrate the multiple ways in which merchants employed visual codes from different social realms (courtly, mercantile, and agrarian) to create their built environments. In Chapter Four, I provide a detailed reconstruction and historical chronology of a late thirteenth century temple in Quanzhou, coastal Fujian Province, and southeastern China, which both echoes and transforms architectural forms of contemporaneous temples in India’s Tamil region.
Piecing together over 300 carvings discovered in the region in light of archaeological and art historical evidence, I develop a chronology of the temple’s history, and propose that Ming forces destroyed the temple scarcely a century after its creation. In Chapter Three, I interpret stone temples patronized by the largest south Indian merchant association, the Ainnurruvar, as being integral to their self-fashioning in India and abroad. While the temples do not project a merchant identity per se, I show that they employ an artistic vocabulary deeply entrenched in the visual language of the Tamil region. Chapter Two looks at other forms through which merchants created a shared mercantile culture, including literary expressions and freestanding sculptural stones. These texts demonstrate that merchants engaged in both elite and non-elite artistic production. Chapter One analyzes the distribution, content, and context of Tamil merchant sponsored inscriptions within the Indian Ocean circuit, focusing on the modern regions of Tamil Nadu, Karnataka, Kerala, and Andhra Pradesh. An appendix offers new translations of important Tamil language mercantile inscriptions discovered throughout south India.
“Infinite Sequences in the Constructive Geometry Of Tenth-Century Hindu Temple Superstructures.”
Datta, Sambit.
Nexus Network Journal 12 (2010): 471-483.
“Evolution and Interconnection: Geometry in Early Temple Architecture.”
Datta, Sambit.
Digital Techniques for Heritage Presentation and Preservation (2021): n. pag.
Mandapa: Its Proportion as a tool in Understanding Indian Temple Architecture
Ragima N Ramachandran
International Journal of Scientific & Engineering Research Volume 10, Issue 7, July-2019
ISSN 2229-5518
The Construction Geometry of Early Javanese Temples
David Beynon, Deakin University
Sambit Datta, Curtin University
Papers presented to the 30th Annual Conference of the Society of Architectural Historians, Australia and New Zealand held on the Gold Coast, Queensland, Australia, July 2-5, 2013.
http://www.griffith.edu.au/conference/sahanz-2013/
“On the Idea of the Mandala as a Governing Device in Indian Architectural Tradition.”
Sonit Bafna,
Journal of the Society of Architectural Historians. 59, no. 1 (2000), 26-49.
Mountain Temples and Temple-Mountains: Masrur
Journal of the Society of Architectural Historians (2006) 65 (1): 26–49.
https://doi.org/10.2307/25068237
Decoding a Hindu Temple
Toronto’s Bochasanwasi Akshar Purushottam Swaminarayan Sanstha (BAPS) Shri Swaminarayan Mandir and the Mandala as a Principle of Design
Krupali Uplekar Krusche
Volume 46, Number 2, 2021 World religions in Canada
Religions mondiales au Canada
URI: https://id.erudit.org/iderudit/1088489ar DOI: https://doi.org/10.7202/1088489ar
Aspects of Indian Art and Architecture
Centre for Historical Studies
M21409
Architecture of India
https://en.wikipedia.org/wiki/Architecture_of_India
Space and Cosmology in the Hindu Temple
Subhash Kak
2002, Vaastu Kaushal: International Symposium on Science and Technology in Ancient Indian Monuments
Hindu Temple Architecture in India
Dr. Vinod Kumar
Sociology, Vallabh Government College, Mandi Himachal Pradesh 175001, India
Studies in Art and ArchitectureISSN 2958-1540
http://www.pioneerpublisher.com/SAA
Volume 3 Number 1 March 2024
https://www.pioneerpublisher.com/SAA/article/view/700
WORKSHOP IN INDIAN ARCHITECTURE
Art 514: Proseminar in Indian Art Fall 2000
Hist. of Art Dept., Jaffe Building 113, Weds. 3-5
Professor Michael W. Meister, Jaffe 308
http://www.arthistory.upenn.edu/fall00/514/syl.html
Archive: The University of Pennsylvania houses a photographic archive of Indian art and architecture (now over 100,000 photographs) as part of the W. Norman Brown South Asia Reference Room on the fifth floor west end of Van Pelt library. To gain access, contact the South Asia bibliographer, David Nelson, or his staff. This Archive should be an integral part of your work this semester.
Intention: This seminar will both introduce you in the remarkable variety of India’s architectural accomplishments and encourage you to discuss the broader issues of how architecture can be designed to express meaning. In the past I have sometimes asked students to divide into groups to work together to frame one area of India’s architecture. Categories have been: Early Indian architecture; South Indian architecture; North Indian architecture; early Islamic architecture in India.
This year, I propose to organize readings around a variety of approaches and methodologies: issues of construction, translation of architectural forms into new materials, architectural symbolism, typology and chronology, and praxis (the use and survival of buildings over time).
I will ask you to work collectively, but on different aspects or examples of the general area, reporting in class on the literature, issues, ideas, and substance appropriate to each.
Books: Four books have been ordered by the Penn Book Center (130 S. 34th St.):
Ananda K. Coomaraswamy, Essays in Early Indian Architecture, ed. Michael W. Meister, Oxford University Press, 1993. (This may now be out of print, but is available in the Fine Arts Library reserve.)
Richard H. Davis, Lives of Indian Images, Princeton, 1997 (Princeton University Press paperback).
James C. Harle, The Art and Architecture of the Indian Subcontinent (Pelican History of Art). New York, 1986.
George Michell, The Hindu Temple: An Introduction to Its Meaning and Forms, New York, 1977 (Chicago University Press paperback).
Other books of interest will be placed on Reserve in the Fischer Fine Arts Library and the South Asia Reading Room in Van Pelt, near the photo archive.
Course assignments: In addition to participation in class discussion, students will be asked to prepareshort reports on reading for presentation in class and to choose an area for research leading to a final presentation and paper.
________________________________
Brief Bibliography of General Surveys:
Batley, Claude. The Design Development of Indian Architecture, 3rd rev. enl. ed., London, 1973.
Brown, Percy. Indian Architecture, vol. 1. Buddhist and Hindu periods, vol. 2. Islamic period, 5th ed., Bombay, 1965-68.
Coomaraswamy, Ananda K. The Arts and Crafts of India and Ceylon. London, 1913.
Coomaraswamy, Ananda K. History of Indian and Indonesian Art. New York, 1927.
Fergusson, James. History of Indian and Eastern Architecture, London, 1876; rev. and ed. by James Burgess, 2 vol., London, 1910.
Herdeg, Klaus. Formal Structure in Indian Architecture, preface by Balkrishna Doshi, New York: Rizzoli, 1990 (1978).
Mayamata. An Indian Treatise on Housing, Architecture, and Iconography, trans. by Bruno Dagens, Delhi, 1985.
Pereira, José. Elements of Indian Architecture, Delhi, 1987.
Tadgell, Christopher. The History of Architecture in India: From the Dawn of Civilization to the End of the Raj, London: Architecture Design and Technology Press, 1990.
Volwahsen, Andreas. Living Architecture: Indian and Living Architecture: Islamic Indian, New York, 1969-70.
Architecture of India
RBSI
https://rarebooksocietyofindia.org/grid-layout.php?t=23
From Sikhara to Sekhari: Building from the Ground Up
Michael W. Meister
Temple Architecture and Imagery of south and southeast Asia

Temple Architecture and Imagery of South and Southeast Asia: Prasadanidhi:
Papers Presented to Professor M.A. Dhaky Hardcover – May 27, 2016
by Parul Pandya Dhar (Author), Gerd J.R. Mevissen (Author)

THE TEMPLE AS PURUSA
STELLA KRAMRISCH
(Plates 1-6)
STUDIES IN INDIAN TEMPLE ARCHITECTURE
Papers presented at a Seminar held in Varanasi, 1967
Edited with an introduction by
PRAMOD CHANDRA
Professor in the Department of Art
The University of Chicago
Virāja
Vedā: Puruṣa Śuktam
Chapter 6 – Description of the Virāṭ Puruṣa—Exposition of the Puruṣa Sūkta
https://www.wisdomlib.org/hinduism/book/the-bhagavata-purana/d/doc1122474.html
Viraj
https://static.hlt.bme.hu/semantics/external/pages/Rta/en.wikipedia.org/wiki/Viraj.html
Purusha
https://en.wikiquote.org/wiki/Purusha
Purusha Sukta
https://en.wikipedia.org/wiki/Purusha_Sukta
Chapter 6: The Purusha Sukta of the Veda
https://www.swami-krishnananda.org/religious.life/religious.life_06.html
Chapter 7: The Doctrine of Creation in the Purusha Sukta
https://www.swami-krishnananda.org/religious.life/religious.life_07.html
Creation Myths
XII—Purusha Sukta: an Aurobindonian Interpretation (A)
http://savitri.in/library/resources/sanatana-dharma/aug-09-2009
Purusha Sukta (Text, Transliteration, Translation and Commentary)
AUTHOR: S.K. RAMACHANDRA RAO
PUBLISHER: SRI AUROBINDO KAPALI SASTRY INSTITUTE OF VEDIC CULTURE
LANGUAGE: SANSKRIT TEXT WITH TRANSLITERATION AND ENGLISH TRANSLATION
EDITION: 2014
ISBN: 8179940462
PAGES: 96

“Cosmogony as Myth in the Vishnu Purāṇa.”
Penner, Hans H.
History of Religions 5, no. 2 (1966): 283–99. http://www.jstor.org/stable/1062116.

Chapter 53 – Importance of studies of Vedas for Varnins; Origin of the universe, of speech and Vedas
https://www.swaminarayan.faith/scriptures/en/satsangi-jeevan/prakran-5/53
The Purusha sukta
by Kamesvara Aiyar, B. V., tr
Publication date 1898
Publisher Madras, G. A. Natesan
English Commentary on Purusha Sukta of Veda
by S K Ramachandra Rao